题目来自“2018-2019 ICPC, NEERC, Southern Subregional Contest”,codeforces上放置了此题:Find a Number
题意:给出两个正整数d,s。找到一个最小的数 n 使得 n%d==0,并且所有的 n 所有位的数字相加和为s。
解题思路:常规想法,BFS搜索,从根节点0开始搜索,逐渐往尾部添加元素,显然会超时。
优化:减少搜索的次数,减枝。BFS的搜索策略已经保证了第一个访问到的且满足条件的数 n 一定是最小值。因此更关心如何减枝,我们定义一个二维布尔类型数组 vis[d][s],其中 vis[i][j] 表示一个数 x、x%d==i、x的所有位上的数字和为 j 是否被找到了。如果找到了,说明我们不需要继续搜索。
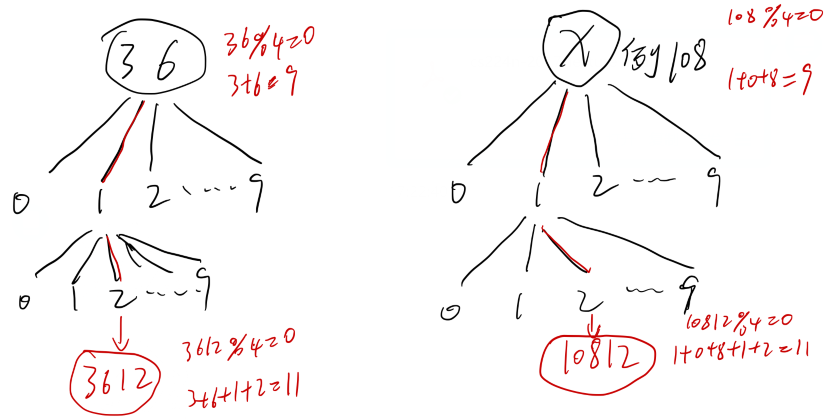
比如 d = 4,s=11,假如我们搜索到36的时候令 vis[0][9]=1 (因为实际上搜索到56就找到答案了), 后面再搜到某个数 x 满足和36一样的条件余数为0,和为9的数字我们都不会加入队列继续搜索,因为 x 的子空间有数满足最终要求,那么 36 的子树也一定包含答案,因为在这个题目里面36和 x 已经没有任何区别,它们的子树除了实际的数值不同外,余数以及每位上的和都相同。并且根据BFS的顺序,36的子树上的答案一定比 x 的子树上的答案小(仔细想想是不是这样~),它通过记录当前的状况是否访问过,从而判断是否要继续搜索。
比如下图。
python代码
#此代码直接放到cf上会超时,这应该是用python的原因导致的,改成C++应该就好了。
#
vis = [[0]*5050 for i in range(505)]
q = [] #(int(n)%d, number_sum, n:str)
d,s = 0,0
q.append((0,0,''))
vis[0][0]=1
z = input()
a = z.split(' ')
d = int(a[0])
s = int(a[1])
def bfs():
cs = [str(i) for i in range(10)]
while q:
now = q[0]
q.pop(0)
for i,j in enumerate(cs):
nxt_mod = (now[0]*10+i)%d
nxt_sum = now[1]+i
nxt_n = now[2]+j
if nxt_mod==0 and nxt_sum==s:
return nxt_n
if not vis[nxt_mod][nxt_sum] and nxt_sum<=s:
q.append((nxt_mod,nxt_sum,nxt_n))
vis[nxt_mod][nxt_sum]=1
return -1
print(bfs())