算法设计15——动态规划，最长公共子序列

动态规划

特征一： 主问题的解包含了子问题的解；

特征二： 子问题出现重叠；

## 前缀动态规划：最长公共子序列（LCS）

•  问题描述：Z是序列X与Y的公共子序列，如果Z是X的子序列也是Y的子序列。
•  Naive方法：
  • 枚举X的每个子序列Z
  • 检查Z是否为Y的子序列
  • T(n)=O(n2m)

•  优化子结构：
• 设X=(x₁, ..., x_m)、Y=(y₁, ..., y_n)是两个序列， LCS_XY=(z₁, ..., z_k)是X与Y的LCS，我们有：
•  如果x_m=y_n, 则z_k=x_m=y_n, LCS_XY = LCS_Xm-1Yn-1 + <x_m=y_n>,   LCS_Xm-1Yn-1是X_m-1和Y_n-1的LCS.    （这个就是最有意思的地方，也就是说LCS_XY的任何前缀 如LCS_XY=(z₁, ..., z_k-1)必然是X_m-1和Y_n-1的LCS（前缀））
•  如果x_m≠y_n，且z_k≠x_m，则LCS_XY是X_m-1和Y的LCS，即 LCS_XY = LCS_Xm-1Y
•  如果x_m≠y_n,且z_k≠y_n,则LCS_XY是X与Y_n-1的LCS，即 LCS_XY = LCS_XYn-1

　　　　

• 子问题重叠性

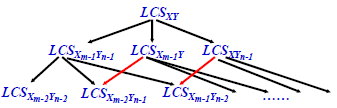
• 方程：

　　　　

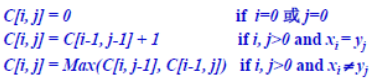
•  自底向上计算：

　　　　

• 伪代码

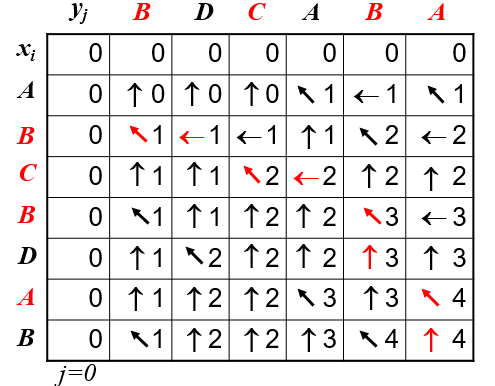
输入：X = (x1,x2,...,xm)，Y = (y1,y2,...yn)
输出：Z = X与Y的最长公共子序列

C[0:m,0:n]: C[i,j]是Xi与Yj的LCS的长度   B[1:m,1:n]:
B[i,j]是指针，指向计算C[i,j]时所选择的子问题的优化解所对应的C表的表项

LCS-length(X, Y)
m←length(X)；n←length(Y)；
For i←0 To m Do C[i,0]←0;
For j←0 To n Do C[0,j]←0;
For i←1 To m Do
  For j←1 To n Do
    If xi = yj
    Then C[i,j]←C[i-1,j-1]+1；B[i,j]←“↖”;
      Else If C[i-1,j]≥C[i,j-1] Then
              C[i,j]←C[i-1,j]; B[i,j]←“↑”;
           Else C[i,j]←C[i,j-1]; B[i,j]←“←”;
Return C and B.

Print-LCS(B, X, i, j)
IF i=0 or j=0 THEN Return;
IF B[i, j]=“↖”
THEN Print-LCS(B, X, i-1, j-1);
    Print xi;
ELSE If B[i, j]=“↑”
    THEN Print-LCS(B, X, i-1, j);
    ELSE Print-LCS(B, X, i, j-1).

Print-LCS(B, X, length(X), length(Y))
      可打印出X与Y的LCS。

• 时间复杂度：
  • 计算代价的时间：O(mn)
  • 构造最优解的时间：O(m+n)
  • 总时间复杂度为： O(mn)
• 空间复杂度：
• 使用数组C和B，需要空间O(mn)

特征一： 主问题的解包含了子问题的解；

 

特征二： 子问题出现重叠；