网络流_Edmond-Karp算法、Dinic算法

转载：网络流基础篇——Edmond-Karp算法             BY纳米黑客

网络流的相关定义：

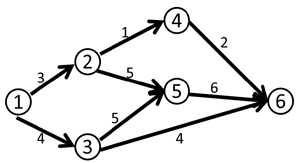
• 源点：有n个点，有m条有向边，有一个点很特殊，只出不进，叫做源点。
• 汇点：另一个点也很特殊，只进不出，叫做汇点。
• 容量和流量：每条有向边上有两个量，容量和流量，从i到j的容量通常用c[i,j]表示,流量则通常是f[i,j].

通常可以把这些边想象成道路，流量就是这条道路的车流量，容量就是道路可承受的最大的车流量。很显然的，流量<=容量。而对于每个不是源点和汇点的点来说，可以类比的想象成没有存储功能的货物的中转站，所有“进入”他们的流量和等于所有从他本身“出去”的流量。

• 最大流：把源点比作工厂的话，问题就是求从工厂最大可以发出多少货物，是不至于超过道路的容量限制，也就是，最大流。

求解思路：

首先，假如所有边上的流量都没有超过容量(不大于容量)，那么就把这一组流量，或者说，这个流，称为一个可行流。

一个最简单的例子就是，零流，即所有的流量都是0的流。

• (1).我们就从这个零流开始考虑，假如有这么一条路，这条路从源点开始一直一段一段的连到了汇点，并且，这条路上的每一段都满足流量<容量，注意，是严格的<,而不是<=。
• (2).那么，我们一定能找到这条路上的每一段的(容量-流量)的值当中的最小值delta。我们把这条路上每一段的流量都加上这个delta，一定可以保证这个流依然是可行流，这是显然的。
• (3).这样我们就得到了一个更大的流，他的流量是之前的流量+delta，而这条路就叫做增广路。我们不断地从起点开始寻找增广路，每次都对其进行增广，直到源点和汇点不连通，也就是找不到增广路为止。
• (4).当找不到增广路的时候，当前的流量就是最大流，这个结论非常重要。

补充：

• (1).寻找增广路的时候我们可以简单的从源点开始做BFS，并不断修改这条路上的delta 量，直到找到源点或者找不到增广路。
• (2).在程序实现的时候，我们通常只是用一个c 数组来记录容量，而不记录流量，当流量+delta 的时候，我们可以通过容量-delta 来实现，以方便程序的实现。

 

相关问题：

为什么要增加反向边？

在做增广路时可能会阻塞后面的增广路，或者说，做增广路本来是有个顺序才能找完最大流的。

但我们是任意找的，为了修正，就每次将流量加在了反向弧上，让后面的流能够进行自我调整。

举例：

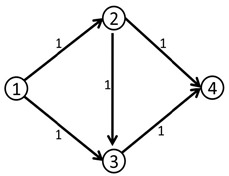
比如说下面这个网络流模型

我们第一次找到了1-2-3-4这条增广路，这条路上的delta值显然是1。

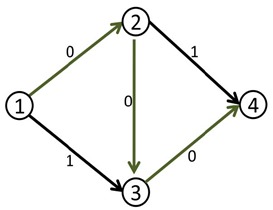
于是我们修改后得到了下面这个流。（图中的数字是容量）

这时候(1,2)和(3,4)边上的流量都等于容量了，我们再也找不到其他的增广路了，当前的流量是1。

但是，

这个答案明显不是最大流，因为我们可以同时走1-2-4和1-3-4，这样可以得到流量为2的流。

那么我们刚刚的算法问题在哪里呢？

问题就在于我们没有给程序一个“后悔”的机会，应该有一个不走(2-3-4)而改走(2-4)的机制。

那么如何解决这个问题呢？

我们利用一个叫做反向边的概念来解决这个问题。即每条边(i,j)都有一条反向边(j,i)，反向边也同样有它的容量。

我们直接来看它是如何解决的：

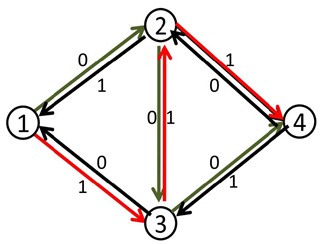
在第一次找到增广路之后，在把路上每一段的容量减少delta的同时，也把每一段上的反方向的容量增加delta。

 

           c[x,y]-=delta;

           c[y,x]+=delta;

我们来看刚才的例子，在找到1-2-3-4这条增广路之后，把容量修改成如下：

这时再找增广路的时候，就会找到1-3-2-4这条可增广量，即delta值为1的可增广路。将这条路增广之后，得到了最大流2。

那么，这么做为什么会是对的呢？

事实上，当我们第二次的增广路走3-2这条反向边的时候，就相当于把2-3这条正向边已经是用了的流量给“退”了回去，不走2-3这条路，而改走从2点出发的其他的路也就是2-4。

如果这里没有2-4怎么办？

这时假如没有2-4这条路的话，最终这条增广路也不会存在，因为他根本不能走到汇点

同时本来在3-4上的流量由1-3-4这条路来“接管”。而最终2-3这条路正向流量1，反向流量1，等于没有流。

附上自己写的Emonks_Karp：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;

const int INF=0xf777;
const int MAXN=1000;

int n,m,ans;
int vis[MAXN],pre[MAXN];
int mp[MAXN][MAXN];

bool bfs(int s,int t)
{
    memset(vis,0,sizeof(vis));
    memset(pre,0,sizeof(pre));
    vis[s]=1;
    queue<int> Q;
    Q.push(s);
    while(!Q.empty())
    {
        int q=Q.front();Q.pop();
        if(q==t) return true;
        for(int i=1;i<=n;i++)
            if(!vis[i]&&mp[q][i])
            {
                vis[i]=1;
                pre[i]=q;
                Q.push(i);
            }
    }
    return false;
}

int Edmonds_Karp(int s,int t)
{
    int ans=0;
    while(bfs(s,t))
    {
        int minn=INF;
        for(int i=t;i!=s;i=pre[i])
            minn=min(minn,mp[pre[i]][i]);
        for(int i=t;i!=s;i=pre[i])
        {
            mp[pre[i]][i]-=minn;
            mp[i][pre[i]]+=minn;
        }
        ans+=minn;
    }
    return ans;
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        mp[x][y]=z;
    }
    printf("%d",Edmonds_Karp(1,n));
    return 0;
}

Dinic算法：

　　ORZ SYCstudio

Dinic算法引入了一个叫做分层图的概念。具体就是对于每一个点，我们根据从源点开始的bfs序列，为每一个点分配一个深度，然后我们进行若干遍dfs寻找增广路，每一次由u推出v必须保证v的深度必须是u的深度+1。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;

const int INF=0x7f7f7f7f;
const int MAXN=400000;

struct Edge
{
    int to,w,next;
}E[MAXN];
int node,head[MAXN],dis[MAXN];
int s,t;
int n,m,ans;

void insert(int u,int v,int w)
{
    E[++node]=(Edge){v,w,head[u]};
    head[u]=node;
    E[++node]=(Edge){u,0,head[v]};
    head[v]=node;
}

bool bfs()
{
    memset(dis,-1,sizeof(dis));
    queue<int> Q;
    Q.push(s);
    dis[s]=0;
    while(!Q.empty())
    {
        int q=Q.front();Q.pop();
        for(int i=head[q];i;i=E[i].next)
            if(E[i].w&&dis[E[i].to]==-1)
            {
                Q.push(E[i].to);
                dis[E[i].to]=dis[q]+1;
            }
    }
    return dis[t]!=-1;
}

int dfs(int x,int flow)
{
    if(x==t) return flow;
    for(int i=head[x];i;i=E[i].next)
        if(E[i].w&&dis[E[i].to]==dis[x]+1)
        {
            int minn=dfs(E[i].to,min(flow,E[i].w));
            if(minn)
            {
                E[i].w-=minn;
                E[i^1].w+=minn;
                return minn;
            }
        }
    return 0;
}

void dinic()
{
    while(bfs()) ans+=dfs(s,INF);
}

int main()
{
    scanf("%d%d%d%d",&n,&m,&s,&t);
    for(int i=1;i<=m;i++)
    {
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        insert(u,v,w);
    }
    dinic();
    printf("%d",ans);
    return 0;
}