(鉴于博客园的表现能力有限,下文中的'^'符合表示集合交,'U'符号表示集合并。'| |'表示集合的元素个数)
对于最基础的容斥原理,就是求满足至少一个条件的事物的数量,即:
设全集中元素有n个属性:a1,a2,...,an,有属性a1的事物的集合为A1,有属性a2的事物的集合为A2,...,有属性an的事物的集合为An,求至少有一个属性的事物的个数,即求|A1UA2U...UAn|
有一个公式(公式1):

证明如下:
 、
、
还有一个等价公式(公式二):
设有 k 种属性,f(S)为至少满足属性集合S的物品个数,同时定义f(∅)=0,则至少有一种属性的物品的个数为:
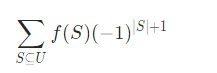
证明:
通过维恩图得知在 k≤3 的时候,公式是十分清晰易懂的,那么在 k 更大的情况下,不妨证明一下为什么这个式子是对的
考虑每一个物品,假设它有 n 个属性,在 n=0 的时候它对答案的贡献只会被 f(∅) 计算到,而且对答案的贡献为 0。
如果n≥1 ,那么可以通过枚举会计算它的贡献的集合来计算它的贡献,那么它的贡献为:
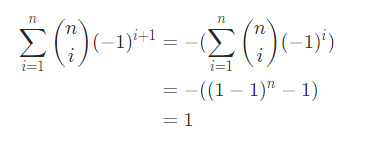
正好为1,因此这个物品如果至少有一个属性的话运用这个公式计算代价时一定会只对答案产生1 的贡献。z
总结:从公式1可以看出,容斥原理求的就是的复杂的多个集合的并集的大小。常搭配的方法求更复杂的集合的并/交集。
下面再补充一个利用补集求交集、并集的方法。

最后补个代码实现吧:
(例题 ,感谢YCH巨佬)

1 for(int s1=1;s1<(1<<k);s1++)//只选哪些长度的环 (状压) 2 { 3 num1=0;//当前选法选的环数 4 tot=0; 5 lcm=1; 6 for(int i=1;i<=k;++i) 7 if(s1&(1<<i-1)) 8 { 9 num1++; 10 tot+=h[i].tot; 11 lcm=1ll*lcm*h[i].len/gcd(lcm,h[i].len); 12 } 13 tot=qpow(tot,n); 14 for(int s2=(s1-1)&s1;s2;s2=(s2-1)&s1)//容斥过程 15 { 16 v=0; 17 num2=0;//要容斥的选法选的环数 18 for(int i=1;i<=k;++i) 19 { 20 if((1<<i-1)&s2) 21 { 22 num2++; 23 v+=h[i].tot; 24 } 25 } 26 v=qpow(v,n); 27 if((num1&1)==(num2&1)) //判断容斥系数 28 tot=(tot+v)%mod; 29 else 30 { 31 tot-=v; 32 if(tot<0) 33 tot+=mod; 34 } 35 } 36 ans=(ans+1ll*tot*lcm%mod)%mod; 37 }
