CF710F String Set Queries [AC自动机+二进制分组]

二进制分组，其实是下面那个玩意，画的粗略了点。

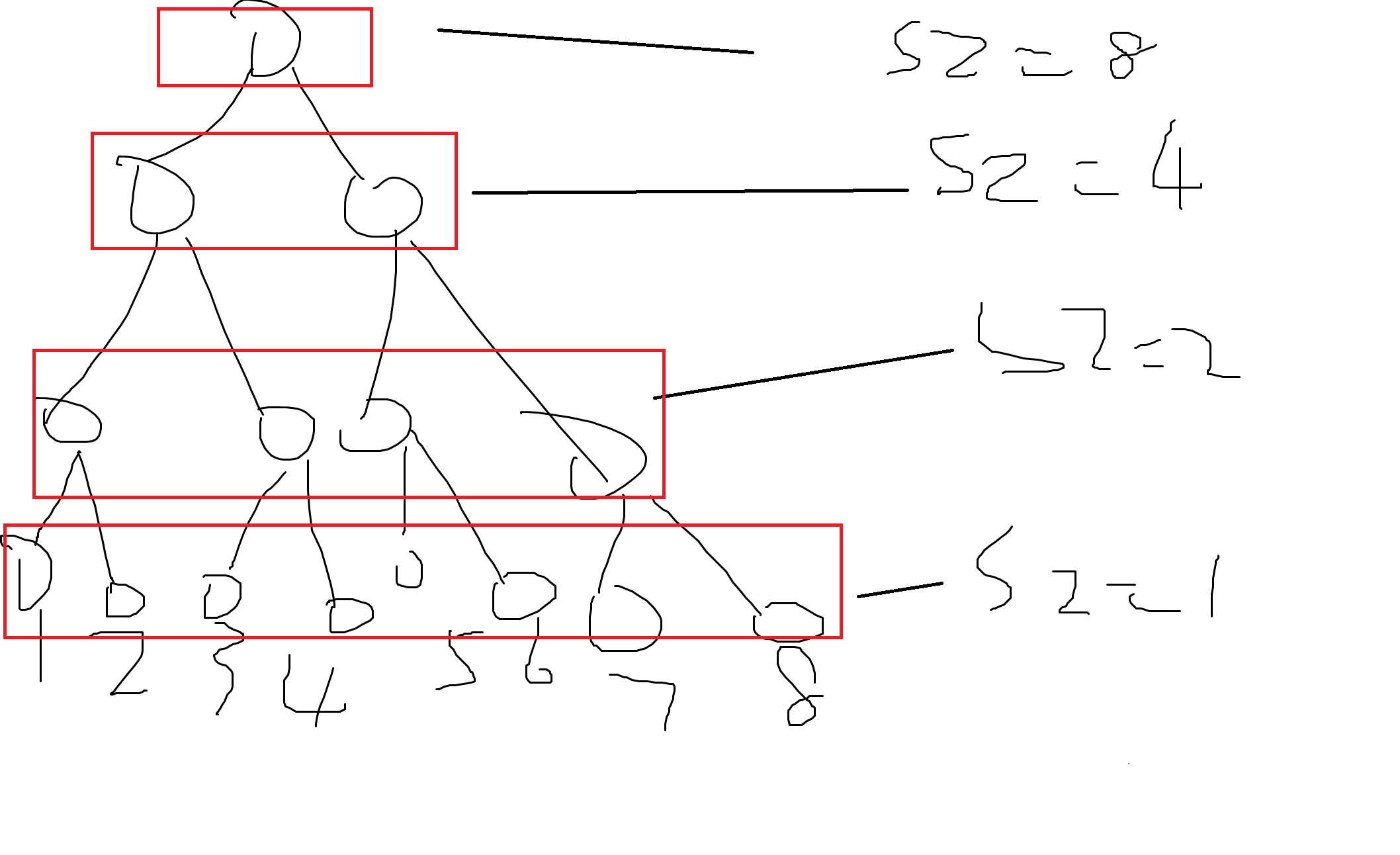
容易证明每个玩意只被合并了 (log) 次，因为有 (log) 层，所以我们可以这样抽象理解他的复杂度是 (n log n) 的。

然后讲一下这题的做法，我们发现你这样每次合并的复杂度是可控的，也就是你可以把 trie 的信息也这么合并，然后对每个点都建一遍 AC 自动机，这样就能做到在线。
至于查询子串次数，我们只需要查询 fail树 从根到自己的 end 个数就好了。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 3e5 + 53;
char s[maxn];
int ch[maxn][26], ed[maxn], fail[maxn], tr[maxn][26], siz[maxn];
int cnt = 1;

struct ACAM {
  int rt, sz;

  void ins(char* s) {
    int p = rt = ++cnt;
    sz = 1;
    while (*s) {
      int c = (*s++) - 'a';
      if (!ch[p][c]) ch[p][c] = ++cnt;
      p = ch[p][c];
    }
    ed[p] = 1;
  }

  void build() {
    queue<int> q;
    for (int i = 0; i < 26; i++)
      if (ch[rt][i]) {
        fail[tr[rt][i] = ch[rt][i]] = rt;
        q.push(tr[rt][i]);
      } else {
        tr[rt][i] = rt;
      }
    while (q.size()) {
      int u = q.front();
      q.pop();
      for (int i = 0; i < 26; i++) {
        if (ch[u][i]) {
          fail[tr[u][i] = ch[u][i]] = tr[fail[u]][i];
          q.push(tr[u][i]);
        } else {
          tr[u][i] = tr[fail[u]][i];
        }
      }
      siz[u] = ed[u] + siz[fail[u]];
    }
  }
};

int merge(int x, int y) {
  if (!x || !y) return x | y;
  ed[x] += ed[y];
  for (int i = 0; i < 26; i++) ch[x][i] = merge(ch[x][i], ch[y][i]);
  return x;
}

struct ACAutoMaton {
  ACAM rt[maxn];
  int top;

  ACAutoMaton() { top = 0; }

  void solve(char* s) {
    rt[++top].ins(s);
    while (top > 1 && rt[top].sz == rt[top - 1].sz) {
      rt[top - 1].rt = merge(rt[top - 1].rt, rt[top].rt);
      rt[top - 1].sz += rt[top].sz, top--;
    }
    rt[top].build();
  }

  int qry(char* s) {
    int ans = 0;
    for (int i = 1; i <= top; i++) {
      int p = rt[i].rt;
      for (char* t = s; *t;) p = tr[p][(*t++) - 'a'], ans += siz[p];
    }
    return ans;
  }
} INS, DEL;

signed main() {
  int _;
  scanf("%d", &_);
  while (_--) {
    int op;
    scanf("%d", &op), scanf("%s", s);
    if (op == 1) {
      INS.solve(s);
    }
    if (op == 2) {
      DEL.solve(s);
    }
    if (op == 3) {
      printf("%d
", INS.qry(s) - DEL.qry(s));
      fflush(stdout);
    }
  }
  return 0;
}