参考
本篇代码参考: https://www.cnblogs.com/xuejianxiyang/p/13821788.html
完整的代码:

public static double[] GetIntersectionPoint( double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4) { //double计算容差 double rong = 1e-8; //因为求斜率需要用除法,分母可能为0,所以求斜率之前, //需要两条线是否x轴平行或者y轴平行 if ((Math.Abs(x2 - x1) < rong) && (Math.Abs(x4 - x3) < rong)) { throw new Exception("与y轴平行,两直线垂直,斜率不存在,无交点"); } if ((Math.Abs(y2 - y1) < rong) && (Math.Abs(y4 - y3) < rong)) { throw new Exception("与x轴平行,两直线水平,斜率为零,无交点"); } //求斜率,分母为0并不报错,而是赋值成 Infinity double a = (y2 - y1) / (x2 - x1); //需考虑分母不能为0 即x2=x1 l1垂直于x轴 double b = (y4 - y3) / (x4 - x3); //需考虑分母不能为0 即x4=x3 l2垂直于x轴 double _x, _y = 0; //L1或L2两直线可能其中一个有Y轴平行(垂直X轴)的 if (Math.Abs(x2 - x1) < rong) //L1垂直于x轴 则x=x1=x2,(x2 - x1)是0==a分母,a=Infinity正无穷 { _x = x1; _y = b * x1 - b * x3 + y3;//公式变换第一种 return new double[] { _x, _y }; } else if (Math.Abs(x4 - x3) < rong) //L2垂直于x轴 则x=x3=x4,(x4 - x3)是0==b分母,b=Infinity正无穷 { _x = x3; _y = a * _x - a * x1 + y1;//公式变换第一种 return new double[] { _x, _y }; } //两条直线都是非垂直状态 /* 知道了点和斜率,那么两条点斜式方程联立. 因为直线方程是一条参照线,两端无限延长,除非平行,否则必有交点. 又因为交点是两条线的共同解,所以点斜式:line1和line2的y相减是0,y=k(_x-x1)+y1 所以未知数y就相减去掉,剩下x,来求y. 反之,也可以相减去掉x,来求y. [y=a(_x-x1)+y1] - [y=b(_x-x3)+y3] =0; [a*(_x-x1)+y1] - [b*(_x-x3)+y3] =0; [a*_x-a*x1+y1] - [b*_x-b*x3+y3] =0; a*_x-a*x1+y1 - b*_x+b*x3-y3 =0; 去括号,+-互变 (a - b)* _x = 0 + a*x1 - y1 - b*x3 + y3; //移项,+-互变 _x = (a * x1 - y1 - b * x3 + y3) / (a - b); */ _x = (a * x1 - y1 - b * x3 + y3) / (a - b); //但是上面程序代码已经算了_x了,直接套入点斜式方程,偷懒...也可以通过公式计算 /* y-y1=k*x-k*x1 y-y1+k*x1=k*x (y-y1+k*x1)/k=x [(y-y1-a*x1)/a] - [(y-y3-b*x3)/b] =0; //这是按照公式的方法 */ _y = a * _x - a * x1 + y1; // 点斜式方程 y-y1=k(x-x1) return new double[] { _x, _y }; }
验证的代码:

static void Main(string[] args) { double[] pt; //水平平衡 pt = 求交点.GetIntersectionPoint(0, 0, 10, 0, 0, 5, 10, 5); Debug.WriteLine(pt[0].ToString() + "," + pt[1].ToString()); //垂直平衡 //pt = 求交点.GetIntersectionPoint(0, 0, 0, 10, 5, 0, 5, 10); //Debug.WriteLine(pt[0].ToString() + "," + pt[1].ToString()); //一斜一水平 //pt = 求交点.GetIntersectionPoint(0, 0, 10, 10, 0, 5, 10, 5); //Debug.WriteLine(pt[0].ToString() + "," + pt[1].ToString()); //一斜一垂直 //pt = 求交点.GetIntersectionPoint(0, 0, 10, 10, 5, 0, 5, 10); //Debug.WriteLine(pt[0].ToString() + "," + pt[1].ToString()); //L1线垂直 //pt = 求交点.GetIntersectionPoint(5, 0, 5, 10, 0, 0, 10, 10); //Debug.WriteLine(pt[0].ToString() + "," + pt[1].ToString()); //L2线垂直 //pt = 求交点.GetIntersectionPoint(0, 0, 10, 10, 5, 0, 5, 10); //Debug.WriteLine(pt[0].ToString() + "," + pt[1].ToString()); //两条都是斜的 //pt = 求交点.GetIntersectionPoint(0, 0, 10, 10, 10, 0, 0, 10); //Debug.WriteLine(pt[0].ToString() + "," + pt[1].ToString()); }
简述
首先要说明,看懂本篇您并不需要高中文化水平.....
为了求两条线的交点,首先要知道什么能求,而目前来说,我只知道高中数学的直线方程,
那么我就要引入直线方程的概念....
然后为什么直线方程能求交点呢?因为同时满足两条联立的直线方程,它的共同解也就只能是交点...(这里没看懂没关系,跟着代码走的时候你就知道了.)
而直线方程实际上是描述一条两端无限延长的线,cad术语就是参照线,构成的两点只是过两点,而不是端点.
是参照线的话,这就有一个非常好的条件: 除非平行,否则必然有交点
那么在编程上,我拿到的数据一般是两个点..(x1,y1)(x2,y2)
通过这一条线坐标计算出斜率,这个斜率实际上就是直角三角形(高/底)
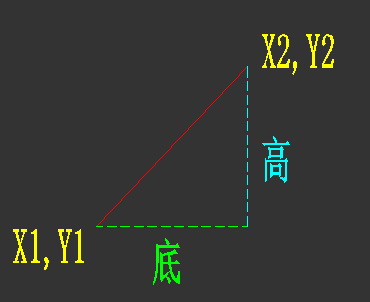
//斜率=高/底
var a = (y2 - y1) / (x2 - x1); //需考虑分母不能为0 var b = (y4 - y3) / (x4 - x3); //需考虑分母不能为0
这样就有个问题了,会存在分母可能为0的情况,需要先判断一下:
//因为求斜率需要用除法,分母可能为0,所以求斜率之前, //需要判断两条线是否x轴平行或者y轴平行 if ((Math.Abs(x2 - x1) < rong) && (Math.Abs(x4 - x3) < rong)) { throw new Exception("与y轴平行,两直线垂直,斜率不存在,无交点"); } if ((Math.Abs(y2 - y1) < rong) && (Math.Abs(y4 - y3) < rong)) { throw new Exception("与x轴平行,两直线水平,斜率为零,无交点"); } //求斜率,分母为0并不报错,而是赋值成 Infinity double a = (y2 - y1) / (x2 - x1); //需考虑分母不能为0 即x2=x1 l1垂直于x轴 double b = (y4 - y3) / (x4 - x3); //需考虑分母不能为0 即x4=x3 l2垂直于x轴
有了斜率和有两个点,就可以求直线方程,可以利用"点斜式"来求.
如果你想知道其他的方式,可以看直线方程的五种形式可看乐乐课堂的 https://www.iqiyi.com/v_19rrdth0kk.html
用我的话来说,其他形式最后都会成为点斜式,因为它足够简单.
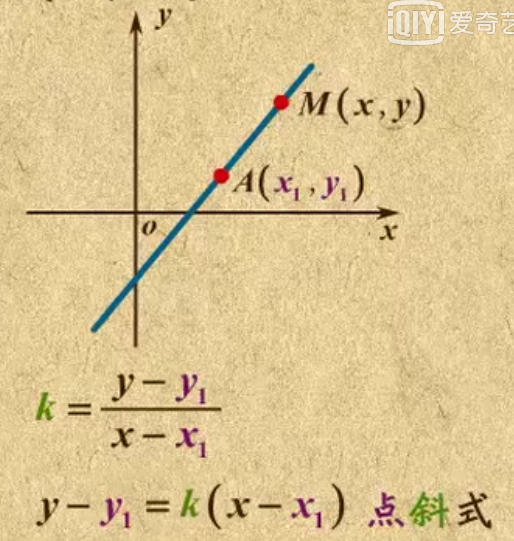
点斜式公式
y-y1=k(x-x1)
这里k是斜率(我的斜率是a和b),可以理解公式的x=x2,y=y2,为了使得x2,y2是个可变的点,所以用x,y代替(我的是_x,_y),成为未知数....这里x1,y1就是套入的点.
如下图,形象理解一下y-y1是竖,x-x1是横,竖=斜率*横
变换成:第一种 y=k(x-x1)+y1 这种比较重要!
变换成:第二种 x=(y-y1-k*x1)/k
然后由于未知数有两个还没法求,但是现在知道了一个条件: {知道x就可以推出y,知道y就可以推出x}
垂线情况
通过垂线得到_x,求出_y
我之前的代码否决了两条线都平行或者都垂直
还有一种情况未否决,这就是其中一条是垂直,它导致了一条线的分母是0,在c#中使用了分母为0的并不报错,而是double的值成为一个Infinity(正无穷)
如果使用了这个斜率就会报错,所以我需要避免使用这个它..
又由于这个斜率为0肯定是一条垂线,它的x1==x2是确定的,代表了两条直线的交点的_x肯定是这个x1.
通过条件{知道x就可以推出y,知道y就可以推出x}套入公式即可求_y
double _x, _y = 0;//未知数初始化 //L1或L2两直线可能其中一个有Y轴平行(垂直X轴)的 if (Math.Abs(x2 - x1) < rong) //L1垂直于x轴 则x=x1=x2,(x2 - x1)是0==斜率a的分母,a=Infinity正无穷 { _x = x1; _y = b * x1 - b * x3 + y3;//公式变换第一种 return new double[] { _x, _y }; } else if (Math.Abs(x4 - x3) < rong) //L2垂直于x轴 则x=x3=x4,(x4 - x3)是0==斜率b的分母,b=Infinity正无穷 { _x = x3; _y = a * _x - a * x1 + y1;//公式变换第一种 return new double[] { _x, _y }; }
联立方程
现在剩下一种情况,就是两条都是斜的.这个时候需要联立方程.
再重复提及一下,因为直线方程描述是一条参照线,两端无限延长,除非平行,否则必有交点.
又因为交点是两条线的共同解,所以点斜式:line1和line2的y相减必然是0.
{第一条线的直线方程} - {第二条线的直线方程} = 0
这样做的目的,就是算式剩下未知数是_x.
套到公式就是这样:
[y=a(_x-x1)+y1] - [y=b(_x-x3)+y3] =0;
[a*(_x-x1)+y1] - [b*(_x-x3)+y3] =0;
[a*_x-a*x1+y1] - [b*_x-b*x3+y3] =0;
a*_x-a*x1+y1 - b*_x+b*x3-y3 =0; 去括号,括号前是-号,故此+-互变
a*_x-b*_x-a*x1+y1+b*x3-y3=0; 未知数的放一块
(a - b)* _x = 0 + a*x1 - y1 - b*x3 + y3; 移项,+-互变
_x = (a * x1 - y1 - b * x3 + y3) / (a - b);
//上面程序代码已经算了_x了,直接套入点斜式方程,通过条件{知道x就可以推出y,知道y就可以推出x}
_y = a * _x - a * x1 + y1;
就这样,大功告成....
编程特有
如果你把这个报错代码去掉,会出现有意思的东西..
if ((Math.Abs(x2 - x1) < rong) && (Math.Abs(x4 - x3) < rong)) { throw new Exception("与y轴平行,两直线垂直,斜率不存在,无交点"); } if ((Math.Abs(y2 - y1) < rong) && (Math.Abs(y4 - y3) < rong)) { throw new Exception("与x轴平行,两直线水平,斜率为零,无交点"); }

