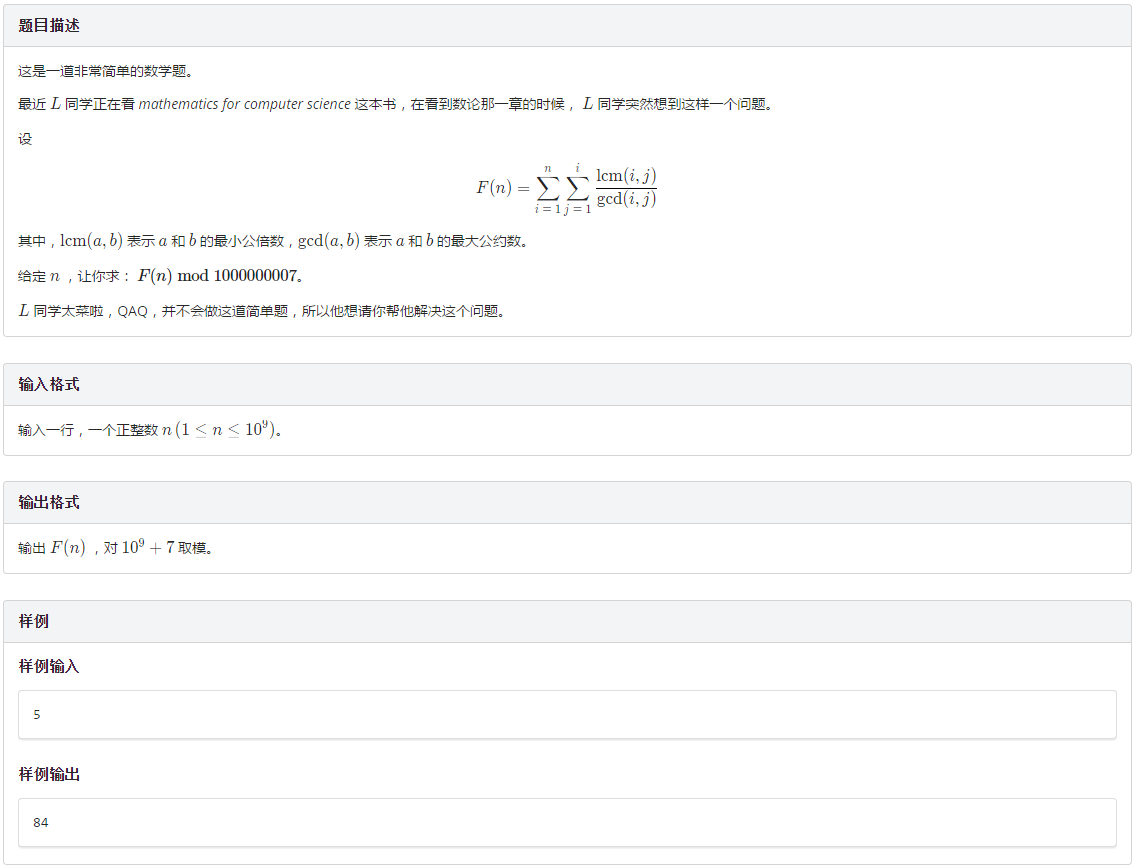
几乎是杜教筛版题,自己想了两种做法,一个和φ有关一个和μ有关,当然只写了第一种,,,至于第二种的话参见jzptab的化简(或者crash的数表),
反正φ和μ卷上1都不难,相信你们都会,这里就懒得说了。。。。。
惊喜的发现自己是rank4之后才意识到这个题只有10个人A了。。。。
#include<bits/stdc++.h>
#define ll long long
#define maxn 1000000
#define ha 1000000007
using namespace std;
const int inv=ha/2+1;
map<int,int> mmp;
int zs[maxn/5],t=0;
int phi[maxn+5];
bool v[maxn+5];
inline int add(int x,int y){
x+=y;
if(x>=ha) return x-ha;
else return x;
}
inline void init(){
phi[1]=1;
for(int i=2;i<=maxn;i++){
if(!v[i]) zs[++t]=i,phi[i]=i-1;
for(int j=1,u;j<=t&&(u=zs[j]*i)<=maxn;j++){
v[u]=1;
if(!(i%zs[j])){
phi[u]=phi[i]*zs[j];
break;
}
phi[u]=phi[i]*(zs[j]-1);
}
}
for(int i=1;i<=maxn;i++){
phi[i]=add(phi[i-1],phi[i]*(ll)i%ha*(ll)i%ha);
}
}
inline int sq(int x){
return x*(ll)x%ha;
}
inline int ci(int x){
ll now=x*(ll)(x+1)>>1ll;
if(!(now%3)) return now/3%ha*(ll)(2*x+1)%ha;
else return now%ha*(ll)((2*x+1)/3)%ha;
}
inline int sum(int x){
if(x<=maxn) return phi[x];
if(mmp.count(x)) return mmp[x];
int an=-sq((x*(ll)(x+1)>>1ll)%ha)+ha;
for(int i=2,j,now;i<=x;i=j+1){
now=x/i,j=x/now;
an=add(an,(ci(j)-ci(i-1)+ha)*(ll)sum(now)%ha);
}
an=-an+ha;
mmp[x]=an;
return an;
}
inline int query(int x){
int an=0;
for(int i=1,j,now;i<=x;i=j+1){
now=x/i,j=x/now;
an=add(an,(sum(j)-sum(i-1)+ha)*(ll)now%ha);
}
return an;
}
int main(){
init();
int n;
cin>>n;
printf("%d
",inv*(ll)(query(n)+n)%ha);
}