improved open set domain adaptation with backpropagation 学习笔记
@
TIP
KL距离,是Kullback-Leibler差异(Kullback-Leibler Divergence)的简称,也叫做相对熵(Relative Entropy)。它衡量的是相同事件空间里的两个概率分布的差异情况。
本文更改了OpenBP中的二元交叉熵损失,提高了识别率。
ABSTRACT
本文对Open set domain adaptation by back propagation(OSDA-BP)中用于提取潜在未知类别样本的二元交叉熵损失进行了深入的研究。基于这种新的理解,我们提出用对称的库勒贝克-莱布勒距离损失来代替二元交叉熵损失。
1.INTRODUCTION AND RELATED WORK
作者透彻详尽地解释了对于OSDA-BP中二元交叉熵损失的理解,并使用对称的KL距离来提出一个新的二元交叉熵损失公式。
2.PROPOSED METHOD
2.1 Overall Idea
本文的方法框架主要还是基于论文《Open set domain adaptation by backpropagation》中的框架。该方法的框图为:
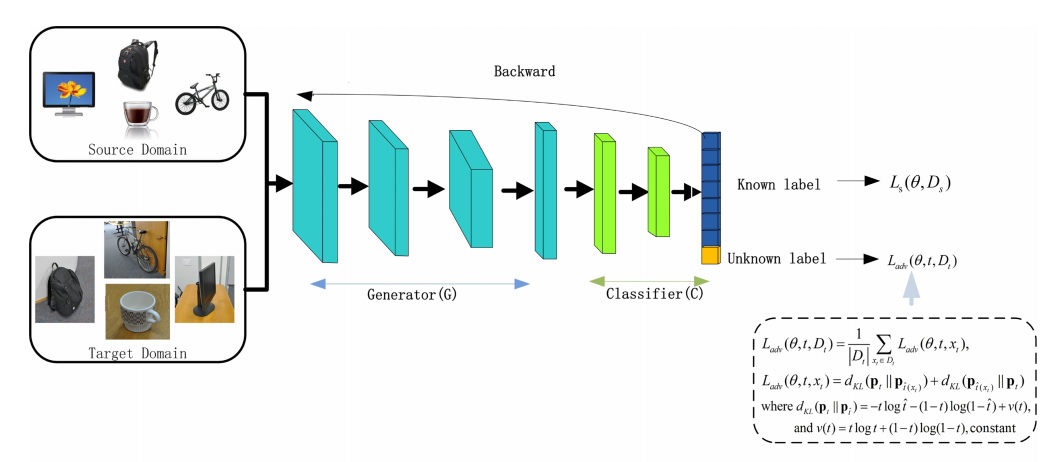
其中源域(D_s={(x^s_i,y^s_i)}^{n_s}_{i=1})拥有(n_s)个已标注的样本,而目标域(D_t={(x^t_i,y^t_i)}^{n_t}_{i=1})拥有(n_t)个未标注的样本,其中x表示样本的图像,y表示样本相对应的标签。源域与目标域之间都存在彼此未拥有的类别。在这样的设定下,作者基于CNN训练网络(f( heta,x)),来将输入的样本(x_s)或者(x_t)分类成K+1类,其中K表示已知类的个数,第K+1类表示未知类。即(f( heta,x)={P(cls(x)=1...P(cls(x)=K+1))}).
模型使用了一个特征提取器与一个分类器,其中(f( heta,x)=C(G( heta_g,x), heta_c))。(( heta_g)表示特征提取器的参数,而( heta_c)表示分类器的参数)
在OpenBP中,首先使用标准交叉熵损失(L_s)来进行源域样本的分类:
(L_s( heta,D_s)=frac{1}{|D_s|}sum limits_{(x_s,y_s)in D_s}l(y_s,f( heta,x_s))),其中的(l(y,f)=-sum limits_{j=1}limits^{K}y_jlog(f_j)),(|D_s|)表示源域样本的个数。
接着OpenBP使用一个二元交叉熵损失(L_u)训练分类器来形成目标域中已知类与未知类之间的边界:(L_u( heta,x_t)=-(1-t)(1-log(P(cls(x_t)=K+1)))-tlog(P(cls(x_t)=K+1))),t的值为0.5.
为了将目标域中未知类别的样本分离,我们还可以使用二元交叉熵损失的平均形式:(L_u( heta,D_t)=frac{1}{|D_t|}sumlimits_{x_tin D_t}L_u( heta,x_t)).
使用(p_t=(t,1-t))来表示一个由t(0<t<1)参数化的二元分布,对于任何目标域样本(x_t),令(hat{t} riangleq P(cls(x_t)=K+1)),且(p_{hat{t}}=(hat{t},1-hat{t}))。则(p_t)与(p_{hat{t}})之间的KL距离为
(d_{KL}(p_t||p_{hat{t}})=tlogfrac{t}{hat{t}}+(1-t)logfrac{1-t}{1-hat{t}}=-tloghat{t}-(1-t)log(1-hat{t})+v(t)).
其中(v(t)=tlogt+(1-t)log(1-t))对于一个固定的t来说是一个固定的值。
上面的二元交叉熵损失(L_u)可以看作为((t,1-t))与((p(cls(x_t)=K+1),1-p(cls(x_t)=K+1))之间除去常数(v(t))的KL距离,通过设置t = 0.5,它为训练好的网络提供了一个合理的机制来区分已知类和未知类。
由于二元交叉熵损失本质上是一个KL距离,我们可以进一步利用它的对称形式:
(L_{adv}( heta,t,D_t)=frac{1}{|D_t|}sumlimits_{x_tin D_t}L_{adv}( heta,t,x_t))
(L_{adv}( heta,t,x_t)=d_{KL}(p_t||p_{hat{t}(x_t)})+d_{KL}(p_{hat{t}(x_t)}||p_t)).
整理之后,总的损失为:
(L( heta,t)=L_s( heta,D_s)+lambda_1L_{adv}( heta,t,D_t)),(lambda_1)=0.5
总的目标函数为:
(minlimits_{ heta_c}L_s( heta,D_s)+lambda_1L_{adv}( heta,t,D_t)).
(minlimits_{ heta_g}L_s( heta,D_s)-lambda_1L_{adv}( heta,t,D_t)).