
最简单的二分查找。最基层!

class Solution {
public:
int search(vector<int>& nums, int target) {
int left=0;
int right=nums.size()-1;
while(left<=right){
int mid=left+(right-left)/2;
if(nums[mid]==target) return mid;
else if(nums[mid]>target){
right=mid-1;
}
else if(nums[mid]<target){
left=mid+1;
}
}
return -1;
}
};
解1:
思路:评论:
简单二分。跟上题本质没啥不同。变换的是left,right,mid的决策条件。
// Forward declaration of isBadVersion API.
bool isBadVersion(int version);
class Solution {
public:
int firstBadVersion(int n) {
int left=1;
int right=n;
int mid=left+(right-left)/2;
while(left<right){
if(!isBadVersion(mid)){
left=mid+1;
}
else{
right=mid;
}
mid=left+(right-left)/2;
}
return left;
}
};
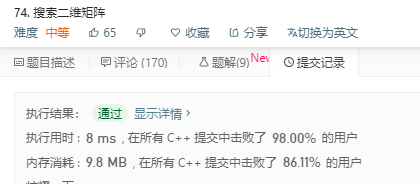
解法1:(自己的代码!)
思路:两次二分查找
注意:开头的两个异常条件很重要,缺一不可。分别判断两个维度的数组是否为空
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
if(matrix.empty()) return false;
if(matrix[0].size()==0) return false;
//先找到外层
int m=matrix.size();
int n=matrix[0].size();
if(matrix[m-1][n-1]<target) return false;
int i;
for(i=0;i<m;i++){
if(matrix[i][n-1]>=target){
break;
}
}
//再找内层,把二维转化为一维
int left=0,right=n-1;
while(left<=right){
int mid=left+(right-left)/2;
if(matrix[i][mid]==target) return true;
else if(matrix[i][mid]>target){
right=mid-1;
}
else if(matrix[i][mid]<target){
left=mid+1;
}
}
return false;
}
};

解法1:
思路: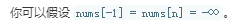 。根据题示,所以如果假如序列是递增的,那么极值就是right。如果是递减的,那么极值就是left。
。根据题示,所以如果假如序列是递增的,那么极值就是right。如果是递减的,那么极值就是left。
而这又可以进一步得到化简。题目中说明只要求一个极值就可以。所以直接判断left 和 left+1 。right 和 right-1 。
接下来就是直接取中间mid 。
可以分为4种情况。
1 3 5
1 3 2
5 3 1
5 3 5
这4种。
分别对应着:
if((nums[mid-1]<nums[mid])&&(nums[mid]>nums[mid+1])) return mid;
if((nums[mid-1]<nums[mid])&&(nums[mid]<nums[mid+1])){
left=mid;
}
if((nums[mid-1]>nums[mid])&&(nums[mid]>nums[mid+1])){
length=mid;
}
if((nums[mid-1]>nums[mid])&&(nums[mid]<nums[mid+1])){
left=mid;
}

class Solution {
public:
int findPeakElement(vector<int>& nums) {
if(nums.empty()||nums.size()==1) return 0;
int left=0;
int length=nums.size()-1;
if(nums[left]>nums[left+1]) return left;
if(nums[length]>nums[length-1]) return length;
while(true){
int mid=left+(length-left)/2;
if((nums[mid-1]<nums[mid])&&(nums[mid]>nums[mid+1])) return mid;
if((nums[mid-1]<nums[mid])&&(nums[mid]<nums[mid+1])){
left=mid;
}
if((nums[mid-1]>nums[mid])&&(nums[mid]>nums[mid+1])){
length=mid;
}
if((nums[mid-1]>nums[mid])&&(nums[mid]<nums[mid+1])){
left=mid;
}
}
return left;
}
};
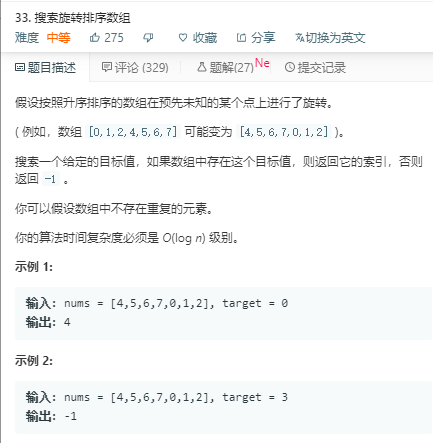
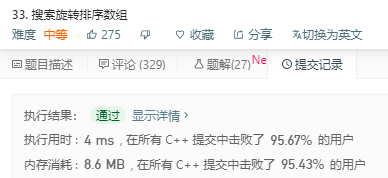
解法1:自己写的代码没想到这么NB!
思路:不好描述。自己再理解一下吧。觉得很快!尤其是添加了while循环中的前两句。主要是if(nums[left]==target) return left;这一句。
二分法加双指针的感觉。如果left指向的不等于target。且left+(right-left)/2得到的mid的值也不等于target 。那么就把left++。再继续判断
(感觉还可以继续优化)
class Solution {
public:
int search(vector<int>& nums, int target) {
if(nums.size()==0) return -1;
if(nums.size()==1&&nums[0]!=target) return -1;
int left=0;
int right=nums.size()-1;
if(nums[right]<target&&target<nums[left]) return -1;
if(nums[right]==target) return right;
if(nums[left]==target) return left;
while(left!=right-1){
if(nums[right]==target) return right;
if(nums[left]==target) return left;
int mid=left+(right-left)/2;
if(nums[mid]==target) return mid;
else if(nums[mid]!=target){
left++;
}
}
if(nums[left]==target){
return left;
}
return -1;
}
};
还应该参考一下别人的思路:
这个题还没有掌握透彻。
解法1:
思路:没想到,和上一题同样的代码。只是返回的是布尔型。可以解决两道题
class Solution {
public:
bool search(vector<int>& nums, int target) {
if(nums.size()==0) return false;
if(nums.size()==1&&nums[0]!=target) return false;
int left=0;
int right=nums.size()-1;
if(nums[right]<target&&target<nums[left]) return false;
if(nums[right]==target) return true;
if(nums[left]==target) return true;
while(left!=right-1){
if(nums[right]==target) return true;
if(nums[left]==target) return true;
int mid=left+(right-left)/2;
if(nums[mid]==target) return true;
else if(nums[mid]!=target){
left++;
}
}
if(nums[left]==target){
return true;
}
return false;
}
};
同样的感觉没有领略到此题的精髓
注意:依次遍历。时间复杂度为O(N) 会超时

解法1:
思路:同上两个题相同。时间复杂度同样没有达到O(logN)。而是O(N/2)
class Solution {
public:
int findMin(vector<int>& nums) {
if(nums.size()==0) return 0;
if(nums.size()==1) return nums[0];
if(nums.size()==2) return min(nums[0],nums[1]);
int left=0;
int right=nums.size()-1;
int little=nums[left];
while(left!=right-1){
little=min(little,nums[left]);
int mid=left+(right-left)/2;
little=min(little,nums[mid]);
left++;
}
little=min(little,nums[right]);
return little;
}
};
解法2:
思路:二分(来自官方题解)

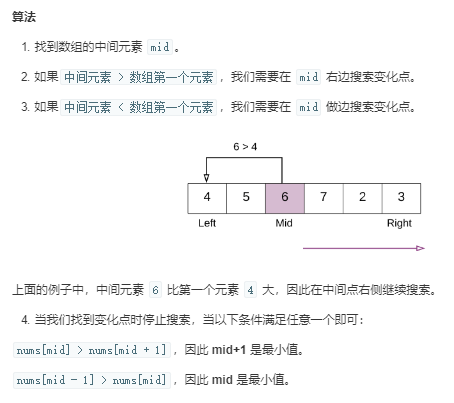
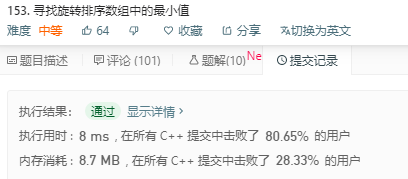
时间复杂度O(logN)
class Solution {
public:
int findMin(vector<int>& nums) {
if(nums.size()==1) return nums[0];
int left=0;
int right=nums.size()-1;
//如果是有序数组
if(nums[left]<nums[right]){
return nums[left];
}
//二分查找:
while(right>=right){
int mid=left+(right-left)/2;
if(nums[mid]>nums[mid+1]) return nums[mid+1];
if(nums[mid-1]>nums[mid]) return nums[mid];
if(nums[mid]>nums[left]){
left=mid+1;
}
else
right=mid-1;
}
return -1;
}
};
解法1:
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
vector<int> res;
for(int i = 0;i<nums1.size();i++){
for(int j=0;j<nums2.size();j++){
if(nums1[i] == nums2[j]){
res.push_back(nums1[i]);
break;
}
}
}
set<int> st(res.begin(),res.end());
res.assign(st.begin(),st.end());//assign函数相当于拷贝函数
return res;
}
};

解法1:

class Solution {
public:
vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
sort(nums1.begin(),nums1.end());
sort(nums2.begin(),nums2.end());
int size1 = nums1.size();
int size2 = nums2.size();
int cur1 = 0, cur2 = 0;
vector<int> result;
while(cur1 < size1 && cur2 < size2){
if(nums1[cur1] == nums2[cur2]){
result.push_back(nums1[cur1]);
cur1++;
cur2++;
}
else if(nums1[cur1] < nums2[cur2]){
cur1++;
}
else if(nums1[cur1] > nums2[cur2]){
cur2++;
}
}
return result;
}
};
解法1:效率低,递归。而且还使用了swap 函数,面试时不能使。
class Solution {
public:
void reverseString(vector<char>& s) {
if(s.empty()){
return;
}
recursive(s,0,s.size()-1);
}
void recursive(vector<char>& s,int start,int end){
if(start > end){
return;
}
recursive(s,start+1,end-1);
swap(s[start],s[end]);
}
};
解法2:
思路:迭代进行交换。双指针
class Solution {
public void reverseString(char[] s) {
int start = 0, end = s.length-1;
char temp;
while(start < end){
temp = s[start];//交换
s[start] = s[end];
s[end] = temp;
start++;
end--;
}
}
}
解法3:双指针 异或交换。
普及一下知识:

class Solution {
public:
void reverseString(vector<char>& s) {
int i = 0, j = s.size() - 1;
while(i < j){
s[i] = s[i] ^ s[j];
s[j] = s[i] ^ s[j];
s[i] = s[i] ^ s[j];
i++;
j--;
}
}
};
