Linear Time: O(n)
Linear time. Running time is proportional to input size. (线性时间: 运行时间与输入大小成正比)
<1>Computing the maximum. Compute maximum of n numbers a1, …, an. (例如,计算最大的数。求n个数字a1,…,an的最大值)

<2>Merge. Combine two sorted lists A = a1,a2,…,an with B = b1,b2,…,bn into sorted whole.


Claim. Merging two lists of size n takes O(n) time.
Proof. After each comparison, the length of output list increases by 1.
O(n log n) Time
O(n log n) time (also referred to as linearithmic time).
<1>Arises in divide-and-conquer algorithms. (出现在分治算法中)
<2>Sorting. Mergesort and heapsort are sorting algorithms that perform O(n log n) comparisons.
<3>Largest empty interval. Given n time-stamps x1, …, xn on which copies of a file arrive at a server, what is largest interval of time when no copies of the file arrive?
(大空的时间间隔。给定n个时间戳x1,…,xn一个文件的副本到达服务器的时间,当文件没有副本到达服务器的最大时间间隔是多少?)
O(n log n) solution: Sort the time-stamps. Scan the sorted list in order, identifying the maximum gap between successive time-stamps.
( O(n log n)的解: 1. 给时间长度排序 2.按顺序扫描排序的列表,识别连续时间戳之间的最大间隙。)
Quadratic Time: O(n^2)
Quadratic time(二次方时间). Enumerate all pairs of elements (枚举所有元素对).
<1>Closest pair of points. Given a list of n points in the plane (x1, y1), …, (xn, yn), find the pair that is closest.
(最接近的一对点。给定平面(x1, y1),…,(xn, yn)中的n个点的列表,找出最接近的那一对)
O(n2) solution.Try all pairs of points.
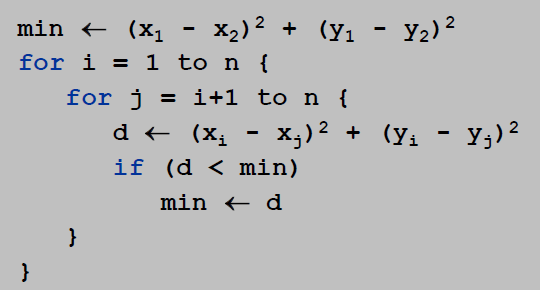
Remark. Ω(n^2) seems inevitable, but this is just an illusion
(备注: Ω(n^2)似乎不可避免,但这只是一个错觉)
Cubic Time: O(n3)
Cubic time(立方时间). Enumerate all triples of elements(枚举所有元素的三元组)
<1> Set disjointness. Given n sets S1, …, Sn each of which is a subset of 1, 2, …, n, is there some pair of these which are disjoint?
(设置剥离。给定n个集合S1,... ,Sn, 每个集合都是1,2,... ,n的子集,是否存在一对不相交的集合?)
O(n^3) solution. For each pairs of sets, determine if they are disjoint.
(O (n ^ 3)解决方案:对于每对集合,判断它们是否不相交)

Polynomial Time: O(n^k) Time
<1>Independent set of size k. Given a graph, are there k (k is a constant) nodes such that no two are joined by an edge?
(大小为k的独立集合: 给定一个图,是否有k个节点使得两个节点之间没有边连接? )
O(n^k) solution. Enumerate all subsets of k nodes.
( O (n ^ k)的解决方案。枚举k个节点的所有子集 )

- Check whether S is an independent set = O(k^2).
- Number of k element subsets = O(k^2*n^k/ k!) = O(n^k). (poly-time for k=17,but not practical)
Exponential Time
<1> Independent set. Given a graph, what is maximum size of an independent set?
(独立集:给定一个图,独立集的最大size是多少?)
<2> O(n^2*2^n) solution. Enumerate all subsets. (列举所有子集)
