最近发现各位大佬们((MikeDuke), (lhm))都早早会了点分治了,我也打算学一下。
讲解博客链接: 点分治略解
博客里面讲得很详细,但我还是觉得(MikeDuke)大佬讲得更易懂一些。
P3806 【模板】点分治1
给定一棵有n个点的树(有边权)
询问树上距离为k的点对是否存在。
运用容斥原理,我们每次找从一个点出发往下找两条路径(可以为空),计入答案,然后进入这个点的每个子树,把算重的部分消去。
消去也比较简单,把每个子树的所有路径找出来(方法同上),把这些路径长度从答案中删去。
为了降低复杂度,我们每次找重心来搞。
(Code:)
void find_root(int cur, int faa) {
f[cur] = 0;
int to;
siz[cur] = 1;
for (register int i = head[cur]; i; i = e[i].nxt) {
to = e[i].to;
if (to == faa || vis[to]) continue;
find_root(to, cur);
siz[cur] += siz[to];
if (siz[to] > f[cur]) {
f[cur] = siz[to];
}
}
if (Siz - siz[cur] > f[cur]) f[cur] = Siz - siz[cur];
if (f[cur] < f[root]) root = cur;
}
void get_dis(int cur, int faa) {
int to;
known_dis[++cnt] = dis[cur];
for (register int i = head[cur]; i; i = e[i].nxt) {
to = e[i].to;
if (vis[to] || to == faa) continue;
dis[to] = dis[cur] + e[i].val;
get_dis(to, cur);
}
}
inline void sol(int cur, int len, int flag) {
cnt = 0;
dis[cur] = len;
get_dis(cur, 0);
for (register int i = 1; i <= cnt; ++i) {
for (register int j = i + 1; j <= cnt; ++j) {
ans[known_dis[i] + known_dis[j]] += flag;
}
}
}
void work(int cur) {
sol(cur, 0, 1); vis[cur] = true;
int to;
for (register int i = head[cur]; i; i = e[i].nxt) {
to = e[i].to;
if (vis[to]) continue;
sol(to, e[i].val, -1);
Siz = siz[to], f[0] = n, root = 0;
find_root(to, cur);
work(root);
}
}
int main() {
//get the data...
Siz = n, f[0] = n, root = 0;
find_root(1, 0);
work(root);
//ans[i]:长度为i的路径条数
return 0;
}
一些习题
T119278 点对游戏(团队题目)
扩展与延伸:动态点分治(点分树)
例题:P2056 [ZJOI2007]捉迷藏
给一棵无根树,一开始全是关键点,然后有若干操作,每次将某关键点改成非关键点,或将某非关键点改成关键点,操作中掺杂着询问。
(n <= 1e5, q <= 5e5)
相当不错的板子题。
双倍经验:P4115 Qtree4
三倍经验:SP2666 QTREE4 - Query on a tree IV
卡常卡的一个比一个厉害
感谢lhm大佬的博客,是这篇博客带领我走入动态点分治的大门(雾 其实是一位山西学长)至少博客里面的板子通俗易懂,十分亲切
- 点分树:点分治时的重心所构成的树
维护三个堆:
q1(维护全局q2各点所统计的答案的最大值),
q2[cur](维护点分树上cur的所有子树的q3[son].top()的值(含一个0(自己连自己)),用时找最大值和次大值相加),
q3[cur](维护点分树上cur所带领的子树连向 fa 的所有边)。
有: (q1=max(q2[].max+q2[].second~max)),(q2[cur] = max(q3[son].max)),$q3[cur] = ${ (dis(node, fa))}(node位于(cur)所带领的连通块)
修改:在点分树上往上跳;对于每个点分树上的点,一级一级地改就行(删掉,更新下一级,加上)
Code
Part Ⅰ:支持删除,查询最大值,次大值的堆:
经常清空更保险。
struct heap{
priority_queue<int> que, wst;//waste
inline void add(int x) {
que.push(x);
}
inline void del(int x) {
wst.push(x);
}
inline void clear() {//attention!!
while (!wst.empty() && que.top() == wst.top()) que.pop(), wst.pop();//attention!!
}
inline int top() {
clear();
if (que.empty()) return -inf;//have problems
return que.top();
}
inline int get_siz() {
clear();
return que.size() - wst.size();
}
inline int get_res() {
clear();
int sz = get_siz();
if (sz == 0) return -1;
if (sz == 1) return 0;
int mx = top();
del(mx);
int res = mx + top();
add(mx);
return res;
}
}q1, q2[N], q3[N];//q3[son]:son -> fa(put res); q2[fa]:fa -> son(get res); q1:ans
Part Ⅱ:动态点分治:
//work前的find_root已经把当前连通块内的点都压入h数组
inline void work(int cur) {
int to; vis[cur] = true; q2[cur].add(0);//收集子树(含自身)的碎链
for (register int i = 1; i <= tot; ++i) {
q3[cur].add(get_dis(h[i], dfzfa[cur]));//给fa当前连通块内的碎链
}
for (register int i = head[cur]; i; i = e[i].nxt) {
to = e[i].to;
if (vis[to]) continue;
tot = 0; Siz = siz[to]; root = 0;//注意tot=0,即 更新h数组
find_root(to, cur);
dfzfa[root] = cur; int rt = root;//注意设定父亲fa(dfzfa)
work(root);
q2[cur].add(q3[rt].top());//收集子树(含自身)的碎链
}
q1.add(q2[cur].get_res());//将该点信息汇总到q1
}
inline void modify(int cur, int type) {//type: 0:add; 1:del
q1.del(q2[cur].get_res());
type ? q2[cur].del(0) : q2[cur].add(0);//change itself
q1.add(q2[cur].get_res());
int np = cur;
while (dfzfa[np]) {
int faa = dfzfa[np]; q1.del(q2[faa].get_res());//删q1
int tmp = q3[np].top(); if (tmp != -inf) q2[faa].del(tmp);//删q2
type ? q3[np].del(get_dis(cur, faa)) : q3[np].add(get_dis(cur, faa));//更新q1
tmp = q3[np].top(); if (tmp != -inf) q2[faa].add(tmp);//更新q2
q1.add(q2[faa].get_res());//更新q1
np = dfzfa[np];
}
}
光为了查个距离还写个树剖?这里有一个不用树剖的方法:把每个点的(点分树上)各级祖先都记录到一个 vector 里面。具体看代码:
int Siz, mxsiz[N], root, h[N], cnt, dfzfa[N], siz[N];
bool vis[N];
vector<int> dis[N];
inline void find_root(int cur, int faa, int nwdis) {//nwdis
dis[cur].push_back(nwdis); h[++cnt] = nwdis;//attention
siz[cur] = 1, mxsiz[cur] = 0;
int to;
for (register int i = head[cur]; i; i = e[i].nxt) {
to = e[i].to;
if (to == faa || vis[to]) continue;
find_root(to, cur, nwdis + e[i].val);
siz[cur] += siz[to];
if (siz[to] > mxsiz[cur]) mxsiz[cur] = siz[to];
}
if (Siz - siz[cur] > mxsiz[cur]) mxsiz[cur] = Siz - siz[cur];
if (mxsiz[cur] < mxsiz[root]) root = cur;
}
void work(int cur) {
int to; vis[cur] = true; q2[cur].add(0);
for (register int i = 1; i <= cnt; ++i) {
q3[cur].add(h[i]); //attention
}
for (register int i = head[cur]; i; i = e[i].nxt) {
to = e[i].to;
if (vis[to]) continue;
cnt = 0; root = 0; Siz = siz[to];
find_root(to, cur, e[i].val);
int rt = root;
dfzfa[rt] = cur;
work(rt);
q2[cur].add(q3[rt].top());
}
q1.add(q2[cur].get_res());
}
bool isbl[N];
inline void modify(int cur, int type) {//type: 0:add; 1:del
q1.del(q2[cur].get_res());
type ? q2[cur].del(0) : q2[cur].add(0);
q1.add(q2[cur].get_res());
int np = cur, id = dis[cur].size() - 1;//id:attention
while (dfzfa[np]) {
int faa = dfzfa[np]; q1.del(q2[faa].get_res());
int tmp = q3[np].top(); if (tmp != -inf) q2[faa].del(tmp);
type ? q3[np].del(dis[cur][id]) : q3[np].add(dis[cur][id]);//dis[][]!!
tmp = q3[np].top(); if (tmp != -inf) q2[faa].add(tmp);
q1.add(q2[faa].get_res());
np = dfzfa[np]; --id; //id-- !!!
}
}
双倍经验?SP2666 QTREE4 - Query on a tree IV
附博客:点分治&&动态点分治学习笔记
例题:P6329 【模板】点分树 | 震波
支持查询与 (x) 相距 (k) 以内的点权和(边权均为1),还需支持单点修改点权。
并不是树上路径问题,只有个“相距”和点分治有点关系。
先考虑静态问题:
对于关于 (x) 的查询,我们可以在 (x) 为分治重心的区域里面查询距离 (x) 小于等于 (k) 的点权和。但是有些合法点超出了 (x) 的管辖区域,那么我们就需要去 (x) 的点分数父亲(以及父亲的父亲...)的分治重心求相距那个重心不超过 (k - dis(fa[x], x)) 的点权和,不过可能会多减去原来就已经算过的点。发现这些点一定只会在上一个重心的管辖范围内,直接减去即可。
我们用一个线段树维护 (rt) 管辖区域中与 (rt) 相距为 (d) 的点权和;再开个线段树维护一下 (rt) 管辖区域中与 (fa[rt]) 相距为 (d) 的点权和。
动态的话,修改查询容斥即可。
距离可以预处理,点分树只用维护 (fa[]) 即可,因为我们只会向上跳。
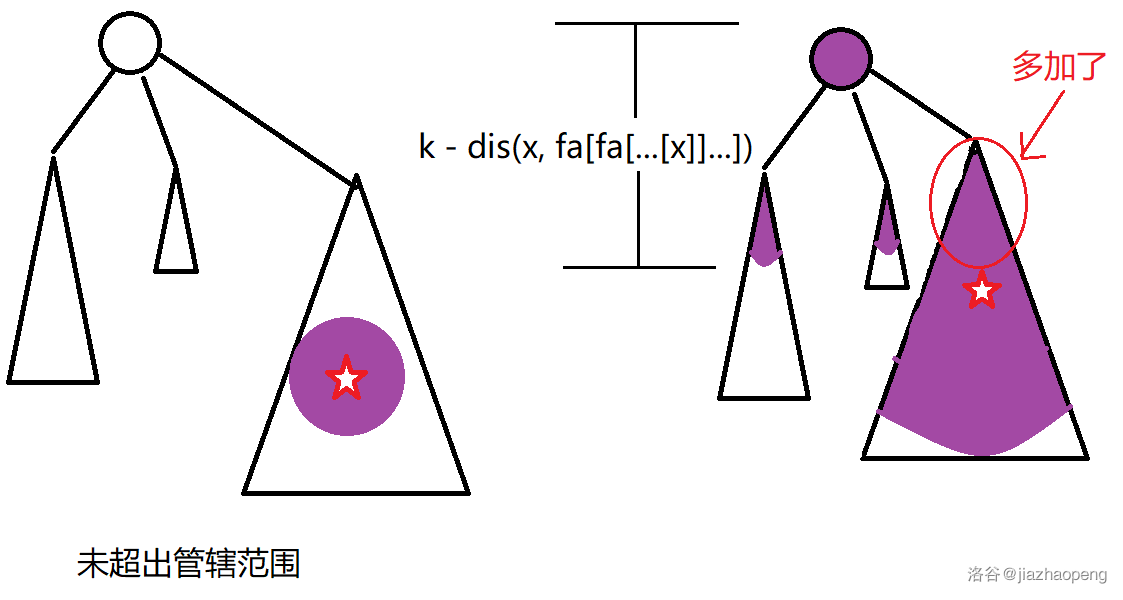
注意查询的时候当前的 (dis) 比 (k) 大,不一定其点分数的祖先都比 (k) 大,或许祖先是在相反方向,反而更近一些。
关键代码:
void dfs(int cur) {
dtot = 0;
fg = true;//打了fg将会把 dfs 到的点的 dis 都存到其 vec 里
dfs_dis(cur, 0, 0);
fg = false;
lim1[cur] = dtot;
build(0, dtot, rt1[cur]);
vis[cur] = true;
for (register int i = head[cur]; i; i = e[i].nxt) {
int to = e[i].to; if (vis[to]) continue;
Siz = siz[to], mxSiz = n;
find_root(to, 0);
int nwroot = root;
fa[root] = cur;
dtot = 0;
dfs_dis(to, 0, 1);
lim2[nwroot] = dtot;
build(0, dtot, rt2[nwroot]);
dfs(nwroot);
}
}
inline void Modify(int p, int v) {
int cha = v - h[p];//Attention!!
h[p] = v;
modify(0, lim1[p], 0, cha, rt1[p]);//Attention!!!!
int lst = p, nw = fa[p];
int nwt = vec[p].size() - 2;
while (nw) {
modify(0, lim1[nw], vec[p][nwt], cha, rt1[nw]);
modify(0, lim2[lst], vec[p][nwt], cha, rt2[lst]);
lst = nw, nw = fa[nw]; --nwt;
}
}
inline int Query(int p, int k) {
int res = query(0, lim1[p], 0, k, rt1[p]);
int lst = p, nw = fa[p];
int nwt = vec[p].size() - 2;
while (nw) {
if (k - vec[p][nwt] >= 0) {//Attention!!!
res += query(0, lim1[nw], 0, k - vec[p][nwt], rt1[nw]);
res -= query(0, lim2[lst], 0, k - vec[p][nwt], rt2[lst]);
}
lst = nw, nw = fa[nw], --nwt;
}
return res;
}
习题
-
幻想乡战略游戏:修改点权,查询加权重心
后续学习:
注意!!!
-
为了防止将子树内部的路径给加上,要么运用容斥,先加后减,要么先一个子树一个子树地计算贡献,计算完一个子树后合并,然后再对子树进行dfs,求子树内部的答案,不要先dfs,再一个子树一个子树地算,很不方便!
-
在求子树的重心时,子树的大小可以暂时按 (siz[to]) 来计算,而不用dfs一遍算它真的siz。至于为什么,见:一种基于错误的寻找重心方法的点分治的复杂度分析
-
计算出子树的重心后,要传重心!!! 不要传 (to) !!!不要dfs(to)!!!!否则就白计算重心了,复杂度会退化成(n^2)!!!
-
注意 (cur) 和 (to) 的区别啊!!!
-
find_root的时候,注意要初始化 (f[](mxsiz[])) 和 (siz[])!! 即:$ siz[cur] = 1; ~ mxson[cur] = 0;$ -
分清to和rt!!!