第一章——集合
一:集合与集合的表示方法
①集合的概念
1.集合:一般地,把一些能够确定的不同的对象看成一个整体,就说这个整体是由这些对象的全体构成的集合,通常用英语大写字母A、B、C来表示。
2.元素:构成集合的每个对象叫做这个集合的元素(或成员),通常用小写字母a、b、c来表示。
3.空集:不含任何元素的集合叫做空集,记作Ø。
②元素与集合的关系
1.属于:如果a是A的元素,就说a属于A,记作a∈A。
2.不属于:如果a不是A的元素,就说a不属于A,记作a∉A。
③集合的特性及分类
1.集合元素的特性:确定性,互异性,无序性
2.集合的分类:
(Ⅰ)有限集:含有有限个元素的集合。
(Ⅱ)无限集:含有无限个元素的集合。
3.常用数集及符号表示:
(Ⅰ)非负整数集(自然数集)——N
(Ⅱ)正整数集——N*或者N﹢
(Ⅲ)整数集——Z
(Ⅳ)有理数集——Q
(Ⅴ)实数集——R
④集合的表示方法
1.列举法:把集合的所有元素一一列举出来,并用花括号"{}"括起来表示集合的方法叫做列举法。
例:第一小组所有男生构成的集合:{小明,小刚}
2.描述法:集合A可以用他的特性p(x)描述为{x∈I|p(x)},表示集合A是由集合I中具有P( x )的所有元素构成的。
例:方程x²-3x+2=0的两个根所构成的集合可以表示为(x∈R|x²-3x+2=0}
⑤重点整合
1.对于集合三性质的掌握程度是关键,是以后所有集合乃至高中数学问题的最基本的点。
2.常用数集符号千万熟背,在后面函数一章中会有很大用。
3.对于集合描述的两种方法要学会相互转化。
4.分类讨论,不重不漏。
二:集合之间的关系与运算
①韦恩图Venn
定义:韦恩图(Venn)是用来反映不同集合之间的交集和并集情况的展示图。一般用于展示2-5个集合之间的交并关系。
长相: 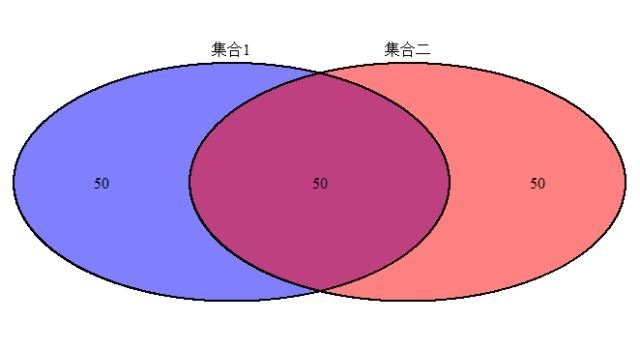
②集合之间的关系
1.子集与真子集:
(Ⅰ)子集:如果集合A中任意一个元素都是集合B的元素,那么集合A叫做集合B的子集,记作A⊆B或B⊇A
(Ⅱ)真子集:如果集合A是集合B的子集,且B中至少有一个元素不属于A,那么集合A叫做集合B的真子集,记作....(我谔谔打不出来,就是包含符号下面的横线变成了不等号)
(Ⅲ)性质:空集是任何一个集合的子集,也就是说对于任何集合都有Ø⊆A
任何一个集合A都是他本身的子集,及A⊆A
如果A⊆B,B⊆C,则A⊆C
如果A不包含于B,B不包含于C,则A不包含于C
2.集合的相等:
(Ⅰ)集合相等的定义:如果集合A的每个元素都是集合B中的元素,反过来,集合B中的每个元素都属于集合A,那么就说集合A和集合B相等,记作A=B
(Ⅱ)集合相等的性质:如果A⊆B,B⊆A,则A=B;番只如果A=B,则A⊆B,B⊆A
③集合的运算
1.交集:一般地,对于两个给定的集合A,B;由属于A又属于B的的所有元素构成的集合叫做A,B的交集,记作A∩B,读作A交B
表示为:A∩B={x|x∈A,且x∈B}
2.并集:一般地,对于两个给定的集合A,B;由两个集合的所有元素构成的集合,叫做A和B的并集,记作A∪B,读作A并B
表示为:A∪B={x|x∈A或x∈B}
3.补集:
(Ⅰ)全集:如果所要研究的集合都是某一给定集合的子集,那么称这个给定集合为全集,通常用符号U表示
(Ⅱ)补集:如果集合A是全集U的一个子集,由U中不属于A的元素构成的集合叫做A在U中的补集,记作∁uA
∁uA={x|x∈U,x|∉A}
④重点整合
1.集合的交并补符号特别是交和并(∩和∪)符号比较易混,需要牢记
2.集合之间的运算是后面求函数值域等等一系列问题的基础,不难,但是要熟练
3.集合之间的关系有时候可以作为突破口推出有用的解题条件,找不到条件的时候别忘了出现的集合