题意
有一张有向图,由一条长度为 T 的链和一个长度为 C 环组成,但是你并不知道 T 和 C 是多少
图的出发点在链的一段,终点在链的另一端,同时终点与一个环相连,大概有点内向树感觉
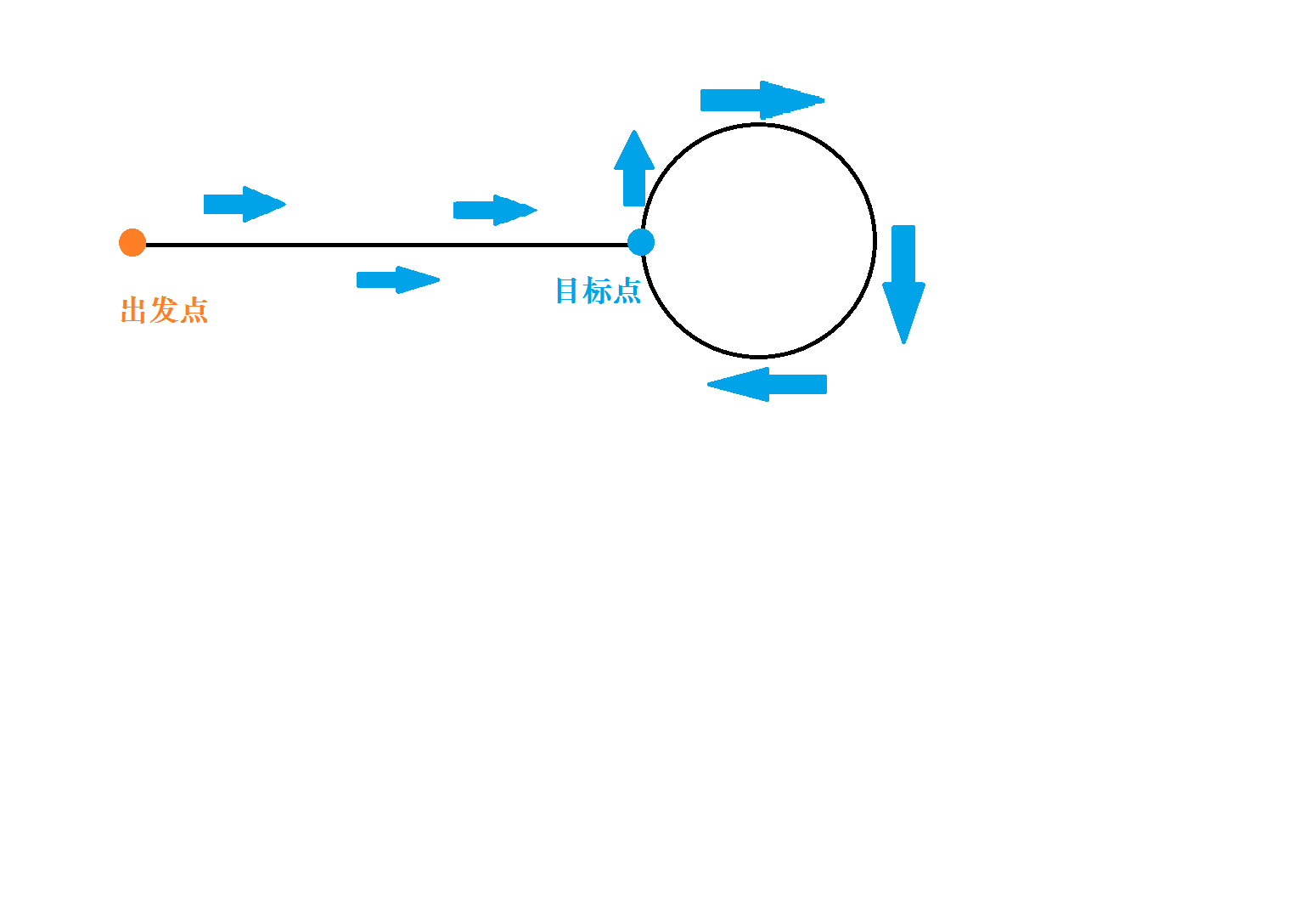
现在有 10 个人,你可以每次操作让一些人沿着路径前进一步,然后交互库会返回你多少个点上有人以及上面的人分别是谁(其实是谁可能不重要?)
你的目标就是在 (3*(T+C)) 次操作内让所有人同时到达终点,然后输出 done
分析
其实很好做?
我们只要首先 重复让 0 号走一步,然后 0 号 1 号一起走一步,直到 0 1 相遇(也就是返回有 2 个点上有人)
不难看出此时 0 1 一定在环上,然后我们让 10 个人一起走,等他们所有人相遇,就是走到终点了
什么?为什么这么做是对的?
我们设 1 走了 (T + x) 步后和 0 相遇 ,那么 0 就走了 (2*(T + x)) (T 就是链长)
那么 (T+x) 必然是 (C) 的倍数,因为 0 1 相遇, 0 肯定在环上多走了几圈
于是 1 号点再走 T 步就能到终点了, 0 和 1 一起走的,看做一个点就好了
而其他所有的点走了 T 步之后也到终点了
虽然我们不知道 T 是多少,但是让他们走着就对了(反正相遇了就是到终点了)
关于交互的问题
首先就是不知道能不能用文件读入...(好像不行,亲测出锅了)
然后就是记得 fflush
当然用 cout + endl 的好像连 fflush 都可以省掉不用了QVQ
//by Judge
#include<bits/stdc++.h>
using namespace std;
inline int read(){ int x=0; char c=getchar();
for(;!isdigit(c);c=getchar());
for(;isdigit(c);c=getchar()) x=x*10+c-'0'; return x;
} char s[15];
inline int get(){ int x=read();
for(int i=1,t;i<=x;++i) scanf("%s",s); return x;
}
int main(){
while(1){
puts("next 0"),fflush(stdout),get();
puts("next 0 1"),fflush(stdout);
if(get()==2) break;
}
while(1){
puts("next 0 1 2 3 4 5 6 7 8 9"),fflush(stdout);
if(get()==1) break;
} return puts("done"),fflush(stdout),0;
}