浅谈树套树(线段树套平衡树)&学习笔记

0XFF 前言

*如果本文有不好的地方，请在下方评论区提出，Qiuly感激不尽！

0X1F 这个东西有啥用?

树套树------线段树套平衡树，可以用于解决待修改区间(K)大的问题，当然也可以用 树套树------树状数组套可持久化线段树，但是 线段树套平衡树 更加容易理解，更加便于新手理解，所以一般也作为树套树的入门类别。
对于静态区间(K)大，我们可以用小巧精悍的主席树来做，也可以用强大无比的(Splay)来做。如果带修改，主席树就无能为力了，(Splay)也会变得很棘手难打。如果用普通线段树，每个节点都有着一课包含子节点的(Splay)，对于一个区间，直接调用线段树上的(Splay)就迎刃而解了。这时的(Splay)不是对全局，而是只对这个线段树节点代表的区间。

当然，树套树------线段树套平衡树并不是那么的好打，还是要动纸笔 and 动脑筋。缺点也是有的：因为要打(Splay)和线段树，模板的码量就有 (150) 行！因为线段树本来就是易手滑的数据结构，稍不留神可能会让你调上好久！另外，因为(Splay)的常数极大，再这么通过线段树一罩，效率就下来了许多，常数巨大无比......总之 树套树 是一个很强的数据结构，但是如果题目不是强制在线的话，(CDQ)分治和整体二分会将树套树吊起来打！
------------Qiuly

---

0X2F 这个东西怎么实现?

首先，线段树套平衡树可以解决的一般问题如下：

• 1. 查询 (k) 在区间 (l,r) 内的排名
• 2. 查询区间 (l,r) 内排名为 (k) 的值
• 3. 修改某一位置上的数值
• 4. 查询 (k) 在区间 (l,r) 内的前驱
• 5. 查询 (k) 在区间 (l,r) 内的后继
• 6. 修改区间 (l,r) 的值(集体加减)(不会)

............

我们今天来讲讲前五个基础操作怎么实现(我只会前五个操作)

0X2f-1 查询 (k) 在区间 (l,r) 内的排名

我们先将一个外面的线段树画下来：

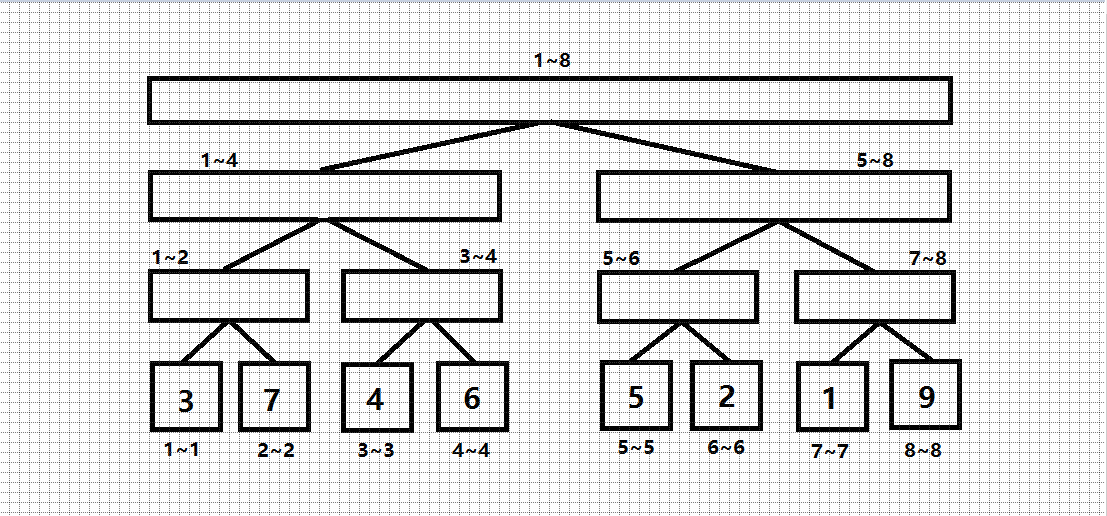
(叶子节点中的数字是序列各个元素的权值)

假设我们现在要查询区间 (3,8) 中 (5) 的排名。

查询一个数的排名，很显然，就是查询这个区间内有多少个数比 Ta 小，然后在+1(即自己)。

那怎么查询 (3,8) 区间内有多少个数比他小呢？(3,8) 不是整个线段树节点啊。

我们可以将它分成若干个线段树节点来处理。

Code:

inline int Splay_rank(int i,int k){//i表示以线段树的i号节点为根的Splay
	int x=rt[i],cal=0;//板子就不再赘述了
	while(x){
	    if(v[x]==k)return cal+((ch[x][0])?s[ch[x][0]]:0);
	    else if(v[x]<k){
	        cal+=((ch[x][0])?s[ch[x][0]]:0)+c[x];x=ch[x][1];
	    }else x=ch[x][0];
	}return cal;
};
inline void Seg_rank(int x,int l,int r,int L,int R,int Kth){
    if(l==L&&r==R){ans+=Splay_rank(x,Kth);return;}//是整个线段树节点
    if(R<=mid)Seg_rank(lc,l,mid,L,R,Kth);//情况1：完全属于左子树
    else if(L>mid)Seg_rank(rc,mid+1,r,L,R,Kth);//情况2：完全属于右子树
    else Seg_rank(lc,l,mid,L,mid,Kth),Seg_rank(rc,mid+1,r,mid+1,R,Kth);//情况3：横跨两子树区间
};

//Main 函数中
case 1:{IN(v);ans=0;Seg_rank(1,1,n,x,y,v);printf("%d
",ans+1);}break;

没看懂？我们来一步一步解读。

首先，进入线段树。

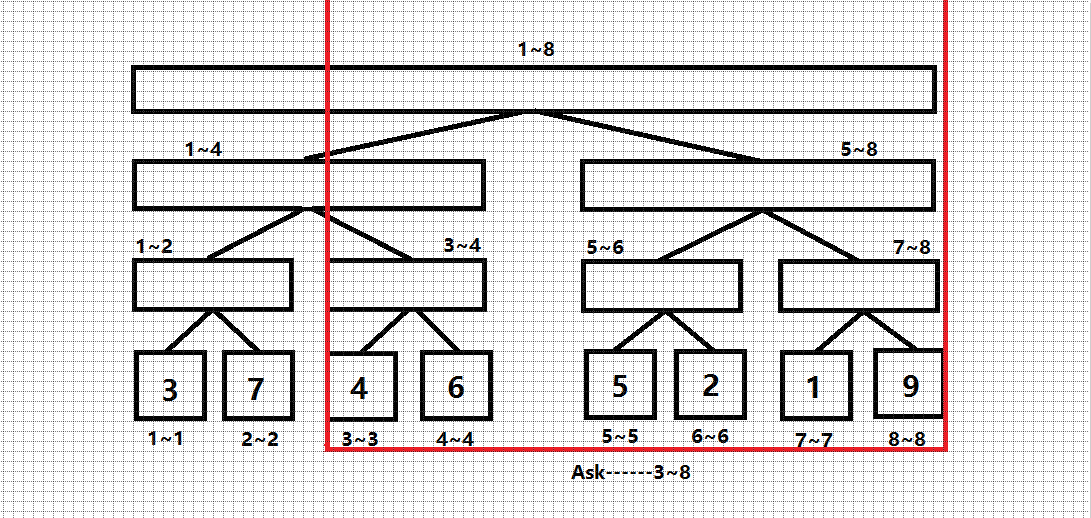
不是整个线段树节点，跳过第一条语句。
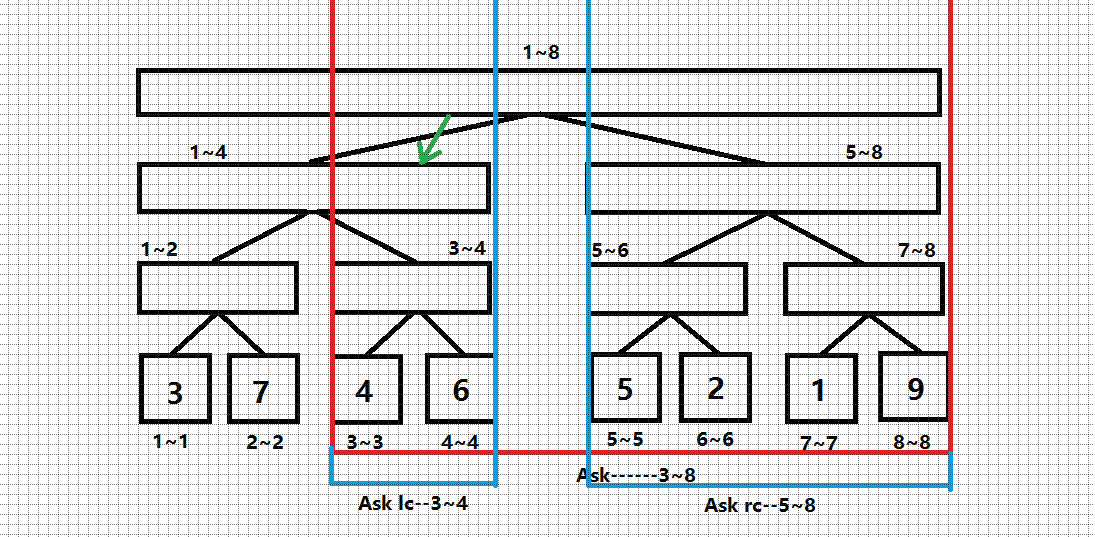
发现 (3,8) 横跨了两个子树，拆开询问区间，先询问左子树。这个时候往左子树递归，目标询问区间 (3,4) ，右子树目标询问区间 (5,8) 。分别处理。

进入左子树：

然后，发现询问区间完全属于右子树(当前区间：(1,4) , 询问区间：(3~4))，所以直接递归右子树：

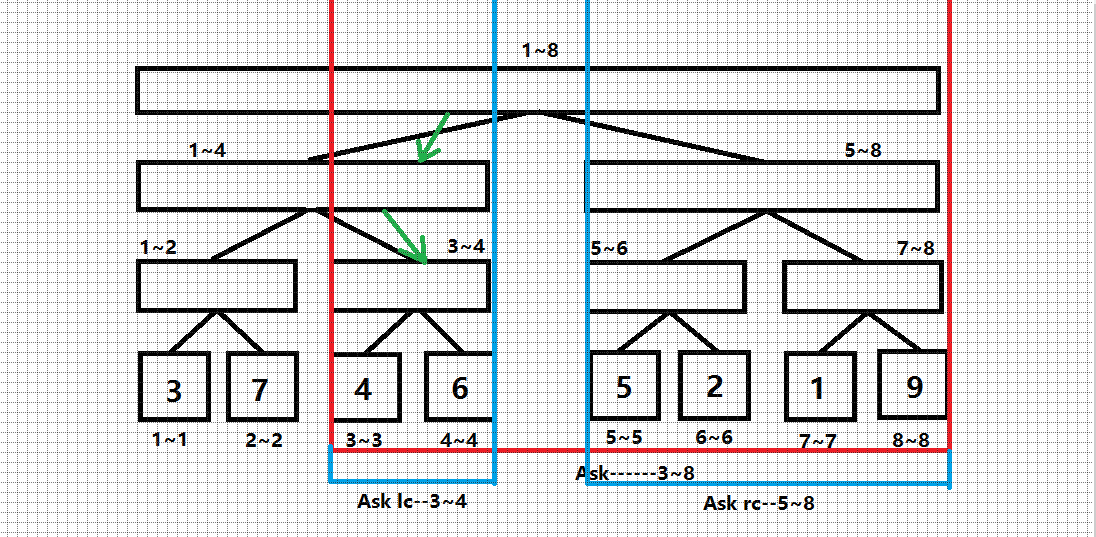
这个时候，发现当前区间和询问区间合并了(当前区间：(3,4) , 询问区间：(3~4))，(Splay) 询问小于 (5) 的数的个数。

区间：(3,4) 的 (Splay) :

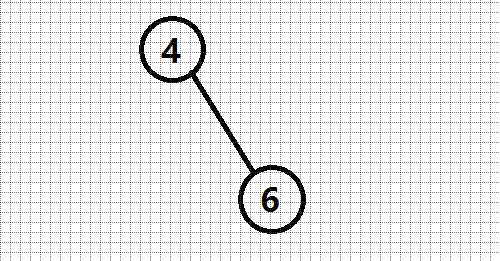
至于 (Splay) 里面的操作不在模拟，因为 ((4,6)) 中比 (5) 小的只有一个数，所以 (ans+=1) ，现在 (ans=1)

左子树的任务完成，现在处理在右子树的询问区间 ((5,8)) ，发现一下去 当前区间：(5,8) , 询问区间：(5,8) 合并了！
直接跳进 (Splay)。

跑完 (Splay) 后，发现有两个数小于 (5) ((=)的不算)，(ans+=2) ，现在 (ans=3) 。

所以询问区间全部处理完了，退出函数。
main函数输出：(ans(3)+1=4) 即答案为 (4) .

---

0X2f-2 查询区间 (l,r) 内排名为 (k) 的值

这个我们需要用到二分来实现，我们不能讲询问区间拆成两个区间(像第一个操作那样)，因为合并不了答案啊。

所以我们依靠二分来实现。

Code:

inline int Get_Kth(int x,int y,int k){
    int L=0,R=MX+1,M;//MX为序列权值的最大值，上图中MX为9.
    while(L<R){
        M=(L+R)>>1;
        ans=0;Seg_rank(1,1,n,x,y,M);//询问M的排名
        if(ans<k)L=M+1;else R=M;//二分
    }return L-1;//return
};

//Main函数中
case 2:{IN(v);printf("%d
",Get_Kth(x,y,v));}break;

这个我就不贴图了，不好画图解释。理解不难，多读几遍代码就好了。

0X2f-3 修改某一位置上的数值

这个很简单，跟普通的线段树单点修改几乎一模一样，只是要同时更新 (Splay)。

inline void Seg_change(int x,int l,int r,int pos,int val){
	Splay_Delete(x,a[pos]);Splay_Insert(x,val);//更新 Splay
    if(l==r){a[pos]=val;return;};//修改序列的值
    if(pos<=mid)Seg_change(lc,l,mid,pos,val);//普通的线段树
    else Seg_change(rc,mid+1,r,pos,val);
};

//Main函数中
case 3:{Seg_change(1,1,n,x,y);}break;

0X2f-4 查询 (k) 在区间 (l,r) 内的前驱

对于这个操作，我们依旧可以拆开来操作，合并的时候对于每个拆分后的询问区间的答案取个最大值，因为是求前驱，肯定是越接近 (k) 越好。

inline void Seg_pre(int x,int l,int r,int L,int R,int val){
    if(l==L&&r==R){ans=max(ans,Splay_Get_pre(x,val));return;}
    if(R<=mid)Seg_pre(lc,l,mid,L,R,val);
    else if(L>mid)Seg_pre(rc,mid+1,r,L,R,val);
    else Seg_pre(lc,l,mid,L,mid,val),Seg_pre(rc,mid+1,r,mid+1,R,val);
};

//Main函数中
case 4:{IN(v);ans=-inf;Seg_pre(1,1,n,x,y,v);printf("%d
",ans);}break;

0X2f-4 查询 (k) 在区间 (l,r) 内的后继

• 跟 (4) 操作同理.

---

0X3F 一些题目

BZOJ3196: Tyvj 1730 二逼平衡树

LUOGU P3380【模板】二逼平衡树(树套树)

这道题就是上面讲的那道啊!

Code:

#include<cstdio>
#include<cmath>
#include<string>
#include<iostream>
#include<algorithm>
#define ll long long
#define RI register int 
#define A printf("A")
#define C printf(" ")
#define inf 2147483647
#define PI 3.1415926535898
using namespace std;
const int N=4e6+2;
//template <typename _Tp> inline _Tp max(const _Tp&x,const _Tp&y){return x>y?x:y;} 
//template <typename _Tp> inline _Tp min(const _Tp&x,const _Tp&y){return x<y?x:y;}
template <typename _Tp> inline void IN(_Tp&x){
    char ch;bool flag=0;x=0;
	while(ch=getchar(),!isdigit(ch))if(ch=='-')flag=1;
	while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
	if(flag)x=-x;
}
int n,m,a[N],ans,MX;
/*----------------------------------Splay-------------------------------------*/
int f[N],c[N],s[N],v[N],ch[N][2],rt[N],tot;
inline int chk(int x){return ch[f[x]][1]==x;};
inline void Splay_del_node(int x){f[x]=s[x]=c[x]=v[x]=ch[x][0]=ch[x][1]=0;};
inline void Splay_pushup(int x){s[x]=(ch[x][0]?s[ch[x][0]]:0)+(ch[x][1]?s[ch[x][1]]:0)+c[x];};
inline void Splay_rotate(int x){
	int y=f[x],z=f[y],k=chk(x),v=ch[x][k^1];
	ch[y][k]=v;if(v)f[v]=y;f[x]=z;if(z)ch[z][chk(y)]=x;
	f[y]=x,ch[x][k^1]=y;Splay_pushup(y),Splay_pushup(x);
};
inline void Splay(int i,int x,int top=0){
	 while(f[x]!=top){
        int y=f[x],z=f[y];
        if(z!=top)Splay_rotate((ch[z][0]==y)==(ch[y][0]==x)?y:x);
        Splay_rotate(x);
    }if(!top)rt[i]=x;
};
inline void Splay_Insert(int i,int x){
	int pos=rt[i];
	if(!rt[i]){
	    rt[i]=pos=++tot;v[pos]=x;s[pos]=c[pos]=1;
        f[pos]=ch[pos][0]=ch[pos][1]=0;return;
	}int last=0;
	while(1){
	    if(v[pos]==x){++c[pos];Splay_pushup(last);break;}
        last=pos;pos=ch[pos][x>v[pos]];
        if(!pos){
            pos=++tot;v[pos]=x;s[pos]=c[pos]=1;
            ch[last][x>v[last]]=pos;
            f[pos]=last;ch[pos][0]=ch[pos][1]=0;
            Splay_pushup(last);break;
        }
	}Splay(i,pos);return;
};
inline int Splay_rank(int i,int k){
	int x=rt[i],cal=0;
	while(x){
	    if(v[x]==k)return cal+((ch[x][0])?s[ch[x][0]]:0);
	    else if(v[x]<k){
	        cal+=((ch[x][0])?s[ch[x][0]]:0)+c[x];x=ch[x][1];
	    }else x=ch[x][0];
	}return cal;
};
inline int Splay_find(int i,int x){
 	int pos=rt[i];while(x){
	    if(v[pos]==x){Splay(i,pos);return pos;};
		pos=ch[pos][x>v[pos]];
	}return 0;
};
inline int Splay_pre(int i){int x=ch[rt[i]][0];while(ch[x][1])x=ch[x][1];return x;}
inline int Splay_suc(int i){int x=ch[rt[i]][1];while(ch[x][0])x=ch[x][0];return x;}
inline int Splay_Get_pre(int i,int x){
    int pos=rt[i];while(pos){
        if(v[pos]<x){if(ans<v[pos])ans=v[pos];pos=ch[pos][1];}
        else pos=ch[pos][0];
    }return ans;
};
inline int Splay_Get_suc(int i,int x){
    int pos=rt[i];while(pos){
        if(v[pos]>x){if(ans>v[pos])ans=v[pos];pos=ch[pos][0];}
        else pos=ch[pos][1];
    }return ans;
};
inline void Splay_Delete(int i,int key){
    int x=Splay_find(i,key);
    if(c[x]>1){--c[x];Splay_pushup(x);return;}
    if(!ch[x][0]&&!ch[x][1]){Splay_del_node(rt[i]);rt[i]=0;return;}
    if(!ch[x][0]){int y=ch[x][1];rt[i]=y;f[y]=0;return;}
	if(!ch[x][1]){int y=ch[x][0];rt[i]=y;f[y]=0;return;}
	int p=Splay_pre(i);int lastrt=rt[i];
	Splay(i,p,0);ch[rt[i]][1]=ch[lastrt][1];f[ch[lastrt][1]]=rt[i];
	Splay_del_node(lastrt);Splay_pushup(rt[i]);
};
/*------------------------------Seg_Tree--------------------------------------*/ 
#define lc ((x)<<1)
#define rc ((x)<<1|1)
#define mid ((l+r)>>1)
inline void Seg_Insert(int x,int l,int r,int pos,int val){
    Splay_Insert(x,val);if(l==r)return;
    if(pos<=mid)Seg_Insert(lc,l,mid,pos,val);
	else Seg_Insert(rc,mid+1,r,pos,val);
};
inline void Seg_rank(int x,int l,int r,int L,int R,int Kth){
    if(l==L&&r==R){ans+=Splay_rank(x,Kth);return;}
    if(R<=mid)Seg_rank(lc,l,mid,L,R,Kth);
    else if(L>mid)Seg_rank(rc,mid+1,r,L,R,Kth);
    else Seg_rank(lc,l,mid,L,mid,Kth),Seg_rank(rc,mid+1,r,mid+1,R,Kth);
};
inline void Seg_change(int x,int l,int r,int pos,int val){
//    printf("QvQ:: %d %d %d %d %d
",x,l,r,pos,val);
	Splay_Delete(x,a[pos]);Splay_Insert(x,val);
    if(l==r){a[pos]=val;return;};
    if(pos<=mid)Seg_change(lc,l,mid,pos,val);
    else Seg_change(rc,mid+1,r,pos,val);
};
inline void Seg_pre(int x,int l,int r,int L,int R,int val){
    if(l==L&&r==R){ans=max(ans,Splay_Get_pre(x,val));return;}
    if(R<=mid)Seg_pre(lc,l,mid,L,R,val);
    else if(L>mid)Seg_pre(rc,mid+1,r,L,R,val);
    else Seg_pre(lc,l,mid,L,mid,val),Seg_pre(rc,mid+1,r,mid+1,R,val);
};
inline void Seg_suc(int x,int l,int r,int L,int R,int val){
    if(l==L&&r==R){ans=min(ans,Splay_Get_suc(x,val));return;}
    if(R<=mid)Seg_suc(lc,l,mid,L,R,val);
    else if(L>mid)Seg_suc(rc,mid+1,r,L,R,val);
    else Seg_suc(lc,l,mid,L,mid,val),Seg_suc(rc,mid+1,r,mid+1,R,val);
};
/*---------------------------------ask----------------------------------------*/
inline int Get_Kth(int x,int y,int k){
    int L=0,R=MX+1,M;
    while(L<R){
        M=(L+R)>>1;
        ans=0;Seg_rank(1,1,n,x,y,M);
        if(ans<k)L=M+1;else R=M;
    }return L-1;
};
/*-------------------------------main-------------------------------------*/
int main(int argc,char const* argv[]){
    IN(n),IN(m);
    for(RI i=1;i<=n;++i){IN(a[i]);Seg_Insert(1,1,n,i,a[i]);MX=max(MX,a[i]);}
    while(m--){
        int op,x,y,v;IN(op),IN(x),IN(y);
        switch(op){
            case 1:{IN(v);ans=0;Seg_rank(1,1,n,x,y,v);printf("%d
",ans+1);}break;
            case 2:{IN(v);printf("%d
",Get_Kth(x,y,v));}break;
            case 3:{Seg_change(1,1,n,x,y);}break;
            case 4:{IN(v);ans=-inf;Seg_pre(1,1,n,x,y,v);printf("%d
",ans);}break;
            case 5:{IN(v);ans=inf;Seg_suc(1,1,n,x,y,v);printf("%d
",ans);}break;
        }
    }return 0;
} 

---

然后就是这道题，跟上面的那道题差不多，大家可以拿来练练手：

BZOJ3196: 1901 Dynamic Rankings

LUOGU P2617 Dynamic Rankings

不贴代码了。

---

一道不错的细节题：

LUOGU P3332 [ZJOI2013]K大数查询

---