python数据可视化分析速成笔记_2-2_布朗运动/几何布朗运动(伊藤过程)实现的demo

第二天/第三天

目标_不分先后:

　实践部分：　　 

• 重点熟悉：numpy，scipy，matplotlib，random，https://docs.spyder-ide.org/

　　实际上如果是熟悉matlab操作的大神们应该改会发现这些包和matlab里面的是相通的

　　python 大杂烩实锤

• 重点

实现问题训练：
• 简单的方程求解曲线参数，模拟图像
• 最小二乘法拟合,回归模型,

　　　了解微分方程模拟

• 解常微分方程，模拟图像
• 解偏微分方程，模拟图像

　　　　时间关系，看看实现例子，然后自己写

• 布朗运动
• 维纳过程
• 几何布朗运动(ito模拟)

• 运用以上模型直接模拟归奥价格走势

　　理论部分：　　

• 复习，推导，理解，几何布朗运动模型，伊藤引理（如果时间不够，跳过这一步）
  1. 期权与股票的性质—
     https://blog.csdn.net/Hellolijunshy/article/details/101028026
  2. 期权的交易策略
  3. 期权二叉树（BSM模型原理的基础和推导就是基于期权二叉树模拟的随机游走过程

              知乎专栏——AI和金融模型——第一篇文章开始

　　　　重点：

1. 维纳过程和伊藤引理
2. BSM，几何布朗运动与布朗运动

时间：24h

 反馈：

• 总体任务完成情况：
  • 大致完成了基本过程，还剩下一个ito没有实现推导，理论没有完全看完，
• 难点：
  • 主要是函数用起来不熟练，而且对函数的目的不了解
  • 微积分不熟，对公式的本质，推导过程理解很浅薄。

一开始不知道用函数怎么实现，还以为布朗运动模拟运动的模拟要积分，实际上运用的是正态分布+时间函数求和，

因为时间点是离散的，用定义法求积分，

dx = a*dt  + b*dz，∑a*dt = T，dz=e*sqrt（dt），e~（0，1），∑dz=（sqrt（dt））*∑ e

伊藤引理也是这样，只是它的积分式是微分方程，由公式：dS/S=u* dt+e* o* sqrt(dt)，求 S ，需要用微分方程来推导

最后会得到几何布朗运动的基本公式

• 收获与反思：
  • 现在可以实现布朗运动/几何布朗运动模拟股市图像，数据还没有找
  • 更加深刻地理解了公式地推导过程
  • 加深了对正态分布的理解,复习了微分方程
  • 实践带动理解
  • 背函数啥的不如直接看大佬们的代码，一行一行理解，反正用的多的就那几个

代码实现:

# -*- coding: utf-8 -*-
"""
Created on Mon May  4 20:43:06 2020

@author: 10913
"""


import numpy as np
import matplotlib.pyplot as plt



'''


几何布朗运动:
    St=S0*exp(ut)
    St=S0*exp(u t+o e sqrt(dt))
    
    St=S0*exp(a t+b z)


'''
D=250   #250个交易日
T=1.0   #总时间1年
dt=T/D   #单位时间

'''
另一种写法
S=np.zeros((M+1,I))

S[0]=S0 #定义S[0]=S0

for t in range(1,M+1):

    S[t]=S[t-1]*np.exp(mean*dt+sigma*np.sqrt(dt)*np.random.standard_normal(I))

'''
s0=100   #初始价格
i=4
st=np.zeros((i,D))
st[0]=s0
a=0.15
b=0.3
n=round(T/dt)#dimension
plt.subplot(212)
for g in range(1, i):
    t=np.linspace(0,T,n)
    e=np.random.standard_normal(size=n)
    z=np.cumsum(e)*np.sqrt(dt)
    x=a*t+b*z;
    st[g]=st[0]*np.exp(z)
    
    plt.plot(t,st[g],label='st'+str(g))
    

plt.legend()
plt.show()

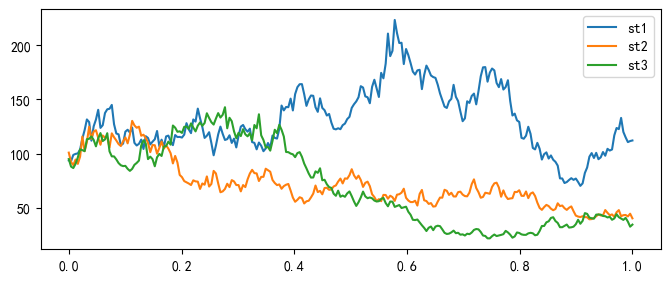
执行结果: