Binary Trees

1. Definiation

What is Binary Trees?

Collection of node (n>=0) and in which no node can have more than two children.

或为空集，或为有一个根节点和两棵互不相交的二叉树组成

左子树与右子树是有顺序的，不能颠倒

即使是只有一颗子树也要分清是左子树还是右子树

2. property

（1）  若二叉树的层次从1开始，则在二叉树的第i 层最多有2^(i-1)个结点；

（2）高度为k 的二叉树最多有2^k-1个结点；

（3）对任一棵二叉树，如果其叶结点个数为n0，度为2的非叶结点个数为n2，则有   n0=n2+1;

（4）具有n个结点的完全二叉树的高度为［logn］+1

（5）

3. 特殊的二叉树

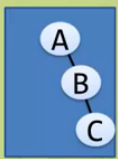
（1）斜树

一波流，要么往左斜，要么往右斜

（2）满二叉树

一颗深度为k且有2^k-1个节点

叶子只能出现在最后一层

（3）完全二叉树

对一颗有n个节点的二叉树编号，如果编号为i的节点与满二叉树的节点编号相同，则这棵树称为完全二叉树

最下层叶子节点一定集中在左部连续

if倒数第二层有叶子节点，则一定在右部连续。

if结点度为一，则一定只有左孩子

同样结点的二叉树，完全二叉树深度是最小的

满二叉树一定是完全二叉树

4、二叉树的储存结构

（1）顺序储存二叉树

完全二叉树

层序遍历，可以用数组表示逻辑结构

 一般二叉树

不存在的结点就用^表示

但如果是斜树呢？

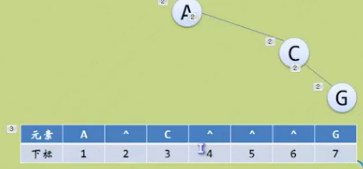
 显然浪费太多的空间

要考虑用链式存储结构

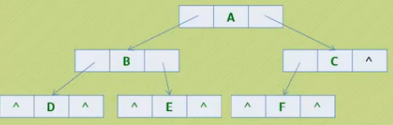
（2）链式储存二叉树

二叉树最多有两个孩子，设计一个数据域和两个指针域，叫做二叉链表

template<typename Object>
struct bitTree
{
    Object data;
    bitTree<Object>*lchild, rchild;
};

5、遍历

What is  遍历？

二叉树的遍历（traversing binary tree）从根结点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点有且只被访问一次。

前序遍历：

若二叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。

 

中序遍历

若树为空，则空操作返回，否则从根结点开始（注并不是先访问根结点），中序遍历根结点的左子树，然后访问根结点，最后中序遍历右子树 

后序遍历

若树为空，则空操作返回，否则从左到右线叶子后结点的方式遍历访问左右子树，最后访问根结点 

层序遍历

一层一层遍历

6、二叉树的建立与遍历算法

//建立二叉树，并输出每个字符所在层数
#include<iostream>
using namespace std;

typedef struct BitNode
{
   char data;
   struct BitNode *lchild, *rchild;
}BitNode, *BitTree;

//创建一棵二叉树，约定用户遵照前序遍历的方式遍历
void CreateBitTree(BitTree *T)
{
   char c;
   cin>>c;

   if(c=='-')
   {
   	*T=NULL;
   }
   else
   {
   	*T=new BitNode();
   	(*T)->data=c;
   	CreateBitTree(&((*T)->lchild));
   	CreateBitTree(&(*T)->rchild));
   }

}

//访问二叉树结点的具体操作
void visit(char data, int level)
{
      cout<<data<<" in "<< level << endl;
}

//前序遍历二叉树
void PreOrderTraversal(BitTree T, int level)
{
	if(T)
	{
		visit(T->data,level);
		PreOrderTraversal(T->lchild,level+1);
		PreOrderTraversal(T->rchild,level+1);
	}
}


//后续遍历删除二叉树
void PostOrderTracersalDelete(BitTree T)
{
	if(T)
	{
		PostOrderTracersalDelete(T->lchild);
		PostOrderTracersalDelete(T->rchild);
		delete T;
	}
}

void play(char data)
{
	cout<<"haha,MidOrderTraversal "<<data<<endl;
}

//中序遍历二叉树
void MidOrderTraversal(BitTree T)
{
      if(T)
      {
      	MidOrderTraversal(T->lchild);
            play(T->data);
            MidOrderTraversal(T->rchild);
      }
}

int main()
{
	int level=1;
	BitTree T=NULL;

	CreateBitTree(&T);     //We have to pass the reference
      PreOrderTraversal(T,level);
      MidOrderTraversal(T);
      PostOrderTracersalDelete(T);

      return 0;
}