fruitful functions "结果"函数 fruitful : 卓有成效的
6.1返回值
6.2 incremental development
这个也很简单,编写比较大的函数时,调试的过程就很费时。我们就可以用到increasemental development,每次测试一小段代码避免过长的调试过程。
假设我们求取 distance = √((x2-x1)**2+(y2-y1)**2)
写出框架:
def distance(x1,y1,x2,y2): return 0.0
添加代码:
def distance(x1,y1,x2,y2): dx = x2 -x1 dy = y2 -y1 print('dx is',dx) print('dy is',dy) return 0.0
继续添加:
def distance(x1,y1,x2,y2): dx = x2 -x1 dy = y2 -y1 dsquared = dx ** 2 + dy ** 2 result = math.sqrt(dsquared) #print(result)作为scaffolding return result
6.3 composition
即在一个函数中调用另一个函数。假设知道圆心与圆上的一点的坐标,求该圆的面积。利用之前的函数可以求得半径。
import math def distance(x1,y1,x2,y2): dx = x2 -x1 dy = y2 -y1 dsquared = dx ** 2 + dy ** 2 result = math.sqrt(dsquared) return result def area(radius): return math.pi * radius ** 2 def circle_area(x1,y1,x2,y2): radius = distance(x1,y1,x2,y2) result = area(radius) return result
6.4布尔函数
6.5more recursion
def factorial(n): if n == 0: return 1 else: recurse = factorial(n-1) result = n * recurse return result
我们可以构建堆栈图,很清楚的就能明白操作过程。
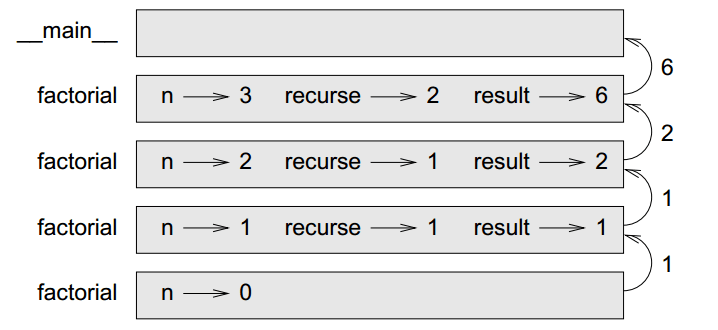
6.6 leap of faith
6.7 one more example
斐波那契函数
def fibonacci(n): if n == 0: return 0 elif n == 1: return 1 else: return fibonacci(n-1) + fibonacci(n-2)
6.8 checking types
求n!时,若参数为非整数或者负数,永远不会得到结果。我们可以:
def factorial(n): if not isinstance(n,int): print('阶乘只定义整型') return None elif n < 0: print('阶乘不能为负数') return None elif n == 0: return 1 else: return n * factorial(n-1)
6.9debugging
对一个函数调试的过程需要考虑以下:
(1)参数有误,不满足先决条件
(2)函数本身有误,不满足后决条件
(3)返回值有误,或使用方式有误
6.11exercise