【机器学习篇】--SVD从初始到应用

SVD一般应用场景--推荐系统，图像压缩。

1、直观感受。

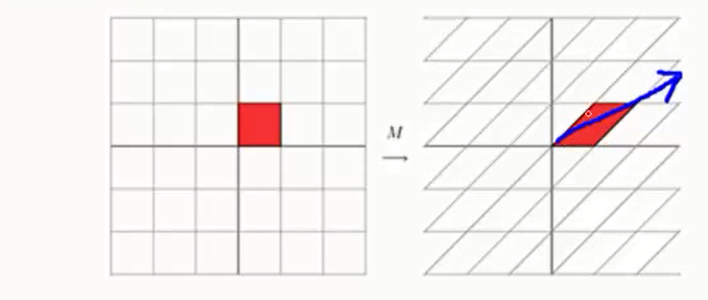
SVD其实就是将矩阵分界，直观感受如图。就是将A矩阵分界成U，S，V三个矩阵相乘。一般推荐系统中用的多。S是对角阵，里面的特征值是从大到小排列的。

2、前述知识。

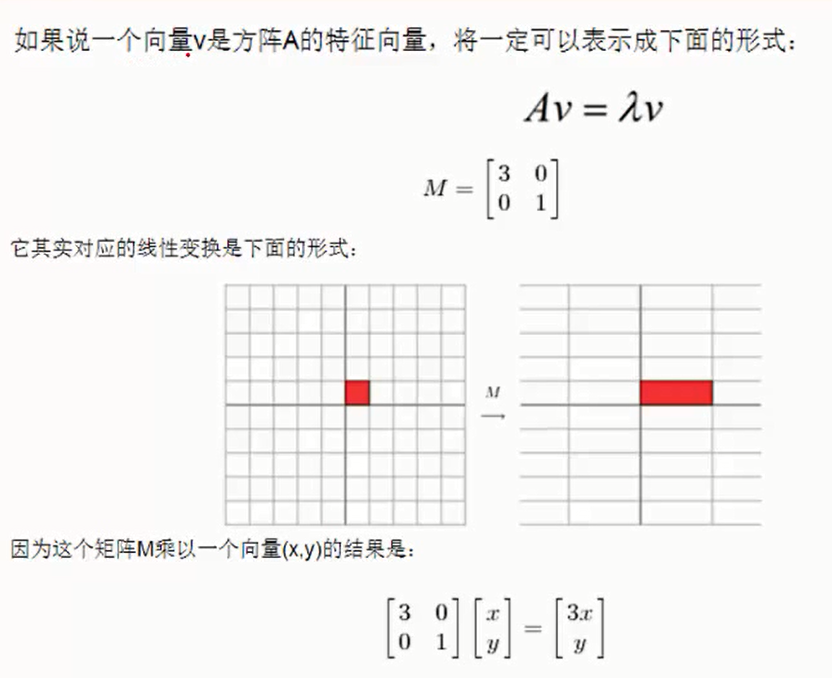
一个矩阵乘以一个向量结果还是一个向量，并且等于原始向量的倍，相当于对原始向量进行一个某个方向上的拉伸。

 3、矩阵压缩

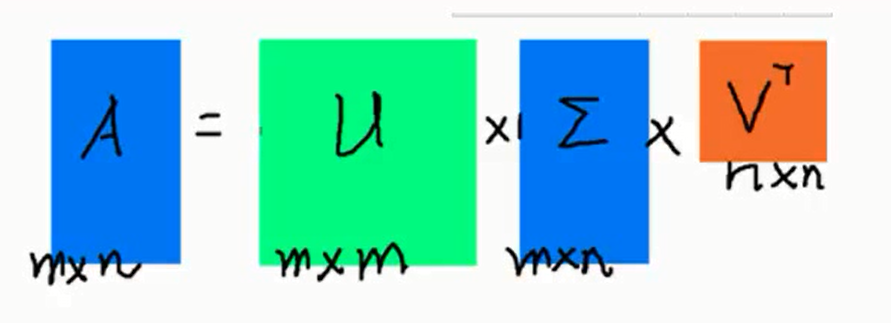
                                    图1

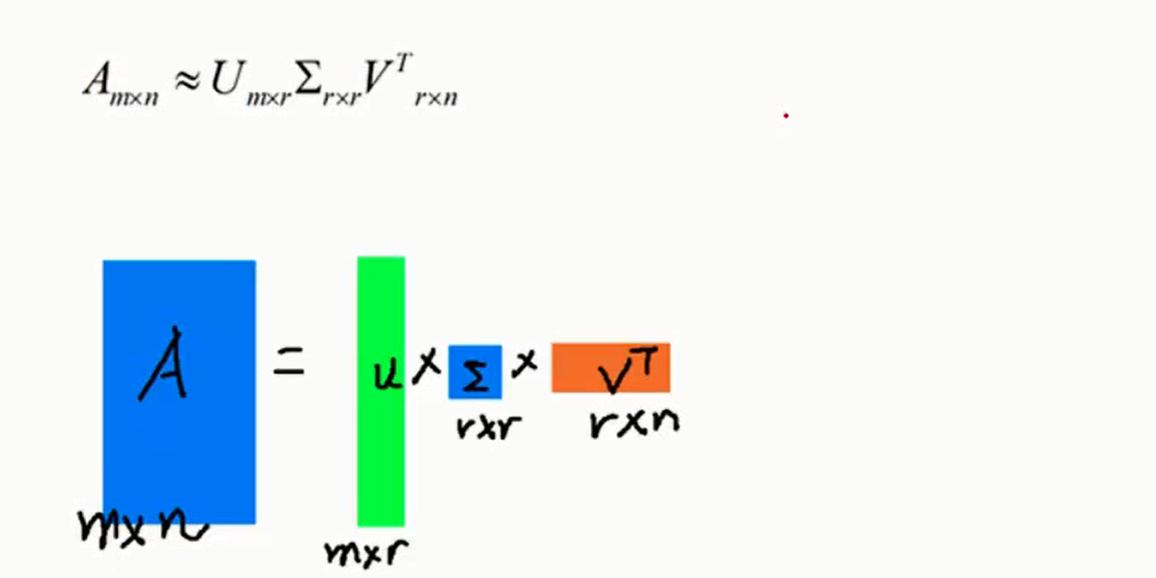
                                 图2

 对图1，图2来说，假设m表示是样本个数，n表示特征个数，则抽取S特征中比较重要的特征值，（因为特征值是从大到小排列的，所以假如抽取前几个特征值作为保留的特征值），则S维度减少，变成r*r,则原始m*n矩阵分解成U ---m*r(比较瘦），S--r*r(方阵)，V--r*n（比较长）三个矩阵相乘。

4、原理剖析

抓住主要变换方向，所以保留特征值比较大的方向。

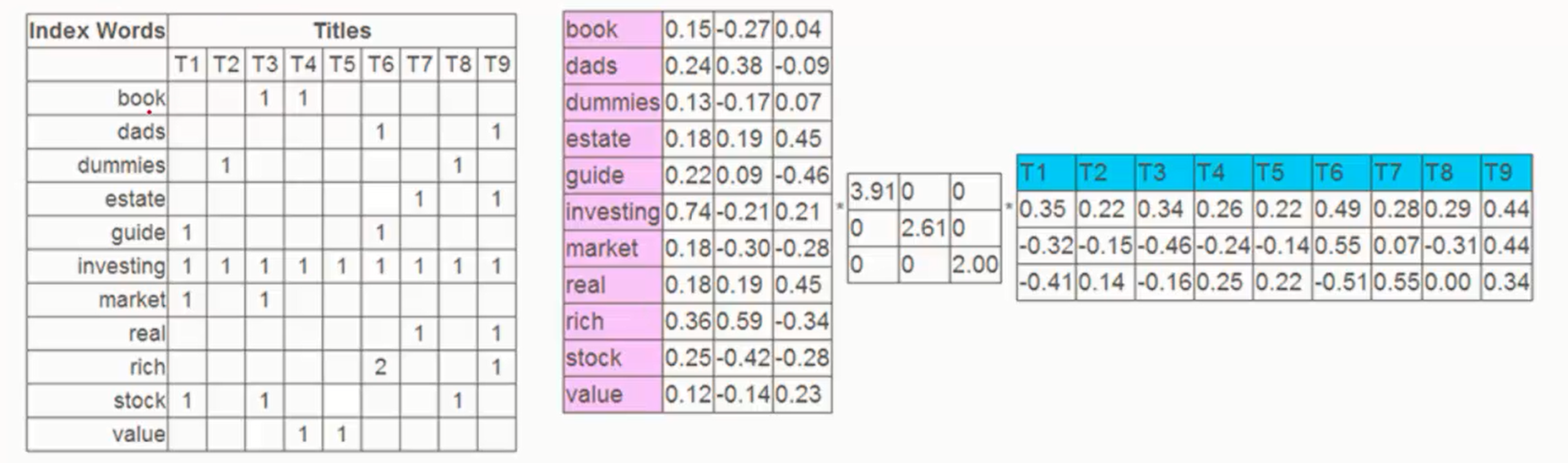
 5、实例讲解一

SVD可解释性比较差，需要去猜。

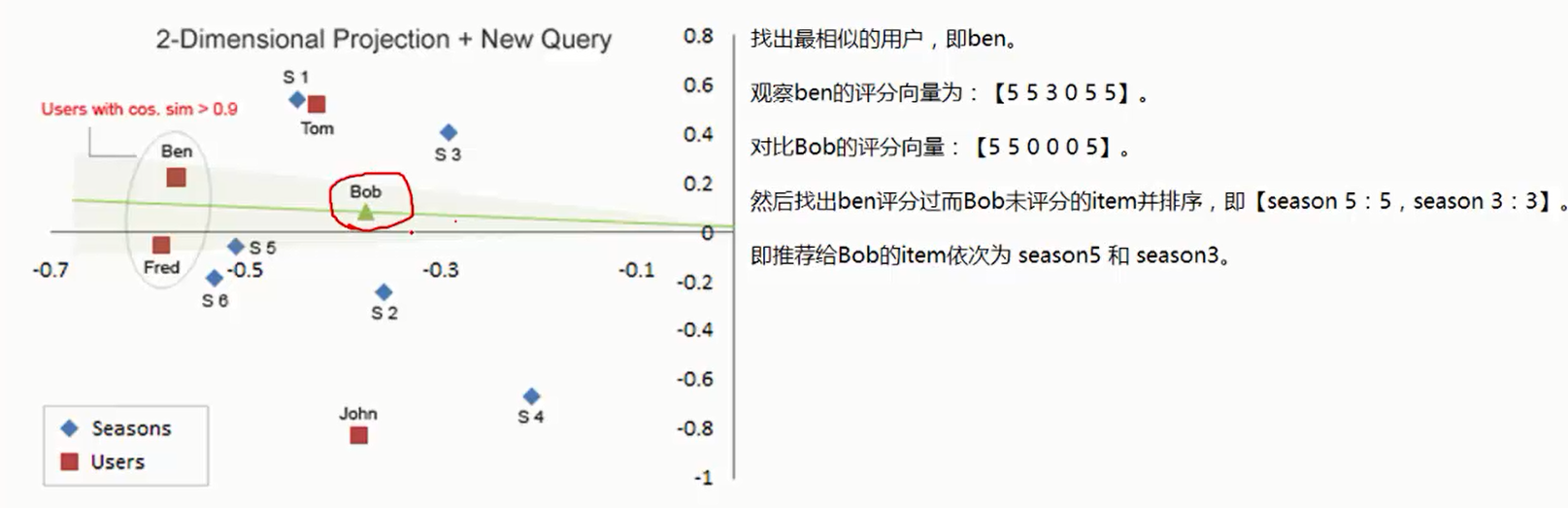
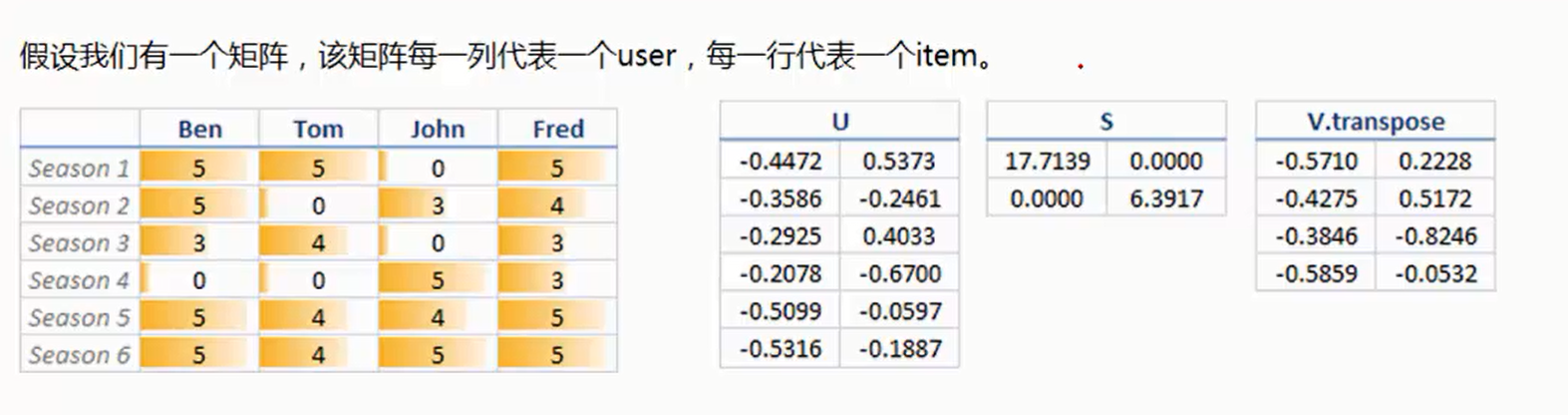
6、实例讲解二（推荐系统）

U ：6*2(6代表是Item个数)

V：4*2（4代表是用户个数）

S：取前两个比较重要的值

 

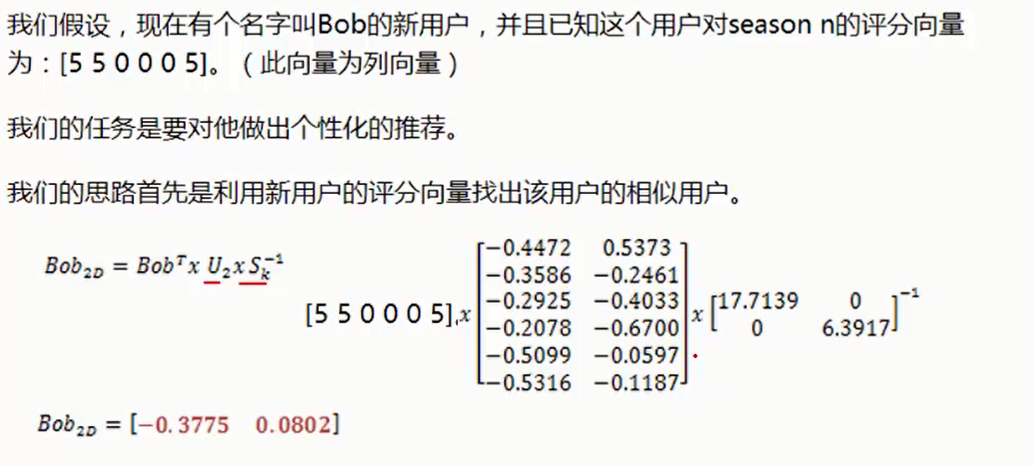
映射到二维图中：找出最相似的用户。