神仙题...
和树的深度有关,由于 $BFS$ 序的性质,显然可以通过把 $BFS$ 序分成若干段来求出深度,每一段就对应某一深度从左到右的所有节点,那么如果确定了分的段数就确定了树的深度(分的段数 $+1$)
为了方便,先把 $BFS$ 序变成从 $1$ 到 $n$ 的序列, $DFS$ 序当然也要随着变一下
考虑每个位置是否可以分段,无非 $3$ 种情况:
$1.$ 此位置必须分,那么对树的深度贡献就是 $1$
$2.$ 此位置不能分,那么贡献就是 $0$
$3.$ 此位置可分可不分,那么贡献就是 $0.5$(此位置分的树的方案数和不分的树的方案数是一样的,如果分贡献 $1$,不分贡献 $0$,那么平均贡献就是 $0.5$)
考虑用 $BFS$ 序和 $DFS$ 序之间的关系求出每个位置的限制,设节点 $i$ 的 $BFS$ 序为 $bfn[i]$,$DFS$ 序为 $dfn[i]$
对于 $BFS$ 序连续的两点 $x,y=x+1$(此时已经按 $bfn$ 重新标号了),如果 $dfn[x]>dfn[y]$ ,说明 $y$ 在 $x$ 的下一层
大概图长这样:

可以发现只有这种情况才会出现 $dfn[x]>dfn[y]$ 的情况,因为如果 $x$ 和 $y$ 在同一层那么显然 $y$ 会更晚被 $dfs$ 到
所以如果 $dfn[x]>dfn[x+1]$,那么 $x$ 和 $x+1$ 之间必须分层
那么如果 $dfn[x]<dfn[x+1]$ ,是否意味着 $x$ 和 $x+1$ 之间不能分层呢,显然是不一定的,对于这种情况我们仍然无法确定是否要分层
可能有两种情况,$x$ 没有儿子, $x+1$ 是 $x$ 的兄弟;$x+1$ 是 $x$ 的儿子,还是没办法确定,而且发现不管是哪种情况都不会对之后的序列产生影响,这保证了无法确定的位置贡献是 $0.5$(这个位置不管切不切方案数都是一样的)
对于 $DFS$ 序连续的两点 $x,y$,情况比较多
如果 $x>y-1$ ($bfn[x]>bfn[y-1]$),那么说明 $y$ 是 $x$ 某个祖先的儿子:

对限制并没有影响
如果 $x==y-1$,那么 $y$ 作为 $x$ 兄弟或者儿子都是合法的
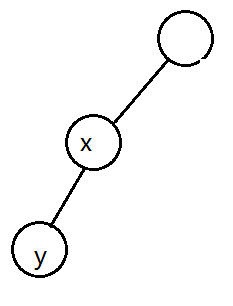
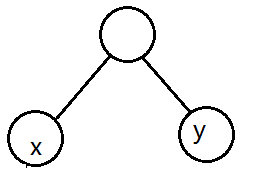
所以仍然无法确定贡献,但是同样可以发现不管是哪种情况对后面的序列都没有影响(里后面节点可以接到 $y$ 下面或者作为 $y$ 的下一个兄弟)
但是第三种情况有点意思:$x<y-1$
说明 $y$ 一定是 $x$ 的第一个儿子:
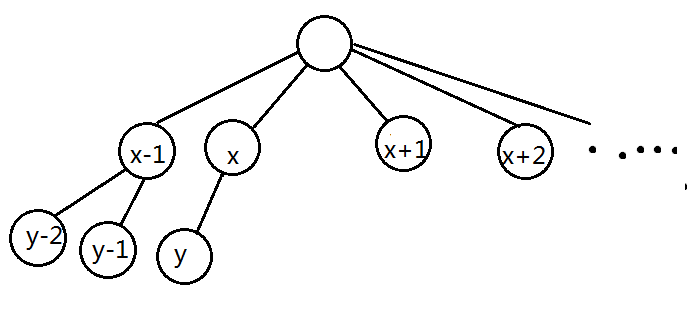
那么就是说,编号从 $x$ 到 $y-1$ 的所有节点深度差不超过1
而且可以发现,如果有分割那么在之前就被计算过了(一定存在 $k$ 使得 $dfn[x+k]>dfn[x+k+1]$ , $x+k in [x+1,y-1]$ )
所以对于 $x<y-1$ 的情况,区间 $[x,y)$ 的位置都不能产生贡献
这个限制可以用一个差分数组维护
最后剩下的都不能确定了,贡献就是 $0.5$
最后一个问题,这些限制是必要的,但是,充分吗?
感性理解一下,很充分,如果怀疑的话打个暴力拍它几个小时,发现没问题,所以是充分的...
并不会证明限制充分 $qwq$
代码很短,但是并不好想...
设 $pos[i]$ 表示 $dfn$ 为 $i$ 的节点(其实就是 $dfn$ 的反数组)
那么对于前面最后一个限制,$x<y-1$,其实就是 $pos[i]<pos[i+1]-1$
注意一开始那些一定要分割的位置已经算过就不会再产生 $0.5$ 的贡献了
还有第一个节点一定单独要分一层
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> using namespace std; typedef long long ll; inline int read() { int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*f; } const int N=2e6+7; int n; double ans; int dfn[N],pos[N],sum[N];//sum是差分数组 //dfn是节点的dfs序,pos是dfn的反数组,所以有 pos[dfn[i]]=i,dfn[pos[i]]=i inline void mark(int x,int y) { sum[x]++,sum[y+1]--; }//打差分标记 int main() { // freopen("1.in","r",stdin); n=read(); ans=1; mark(1,1);//第一个节点一定要分一层 for(int i=1;i<=n;i++) dfn[read()]=i;//读入初始dfs序 for(int i=1;i<=n;i++) pos[dfn[read()]]=i;//用初始dfs序更新变化后的pos //上面一行不太好想。因为bfs序重标号了,原来的节点read()就变成了i,所以pos[dfn[read()]]=i for(int i=1;i<=n;i++) dfn[pos[i]]=i;//用更新后的pos更新dfn for(int i=1;i<n;i++)//注意i不取n { if(dfn[i]>dfn[i+1]) ans++,mark(i,i);//注意这里也要打标记,之后不会再产生0.5的贡献 if(pos[i]<pos[i+1]-1) mark(pos[i],pos[i+1]-1);//打标记 } int now=0; for(int i=1;i<n;i++) now+=sum[i],ans+=(now ? 0 : 0.5);//如果这个位置不确定则贡献为0.5 //注意上一行i不取n,因为切的位置只有n-1个 ans+=1;//深度等于分的段数+1 printf("%.3lf %.3lf %.3lf",ans-0.001,ans,ans+0.001);//BZOJ上要这样输出... return 0; }