在数轴上找一点使得该点到所有其他点的距离之和最小

方法:找到大小为中位数的点,该点就是要求的点(如有两个取之间任意一点都行)
证明:
先看看当只有2个点时的情况:

分类讨论:
如果在A的左边(如 $P_1$ ),距离之和( $sum$ )为:$dis(P_1,A)+dis(P_1,B)=dis(P_1,A)+dis(P_1,A)+dis(A,B)$
( $dis(a,b)$ 为 $a$ 到 $b$ 的距离)
如果在 $A$ 和 $B$ 的中间(包括 $A,B$): $sum=dis(P_2,A)+dis(P_2,B)=dis(A,B)$
如果在右边: $sum=dis(P_3,A)+dis(P_3,B)=dis(A,B)+dis(P_3,B)+dis(P_3,B)$
显然在 $A$ 和 $B$ 中间时距离之和最小。
那对于 $3$ 个点时呢:

设中间的点为 $C$ ,旁边的为 $A,B$
一个点 $P$ 到各个点的距离之和为: $dis(A,P)+dis(B,P)+dis(C,P)=(dis(A,P)+dis(B,P))+dis(C,P)$
如果在能够满足 $dis(A,P)+dis(B,P)$ 最小的情况下还能满足 $dis(C,P)$ 最小,那么就一定是最优的方案
显然 当 $P$ 在 $A,B$ 中间时满足 $dis(A,P)+dis(B,P)$ 最小,
又因为 点 $C$ 在 $A,B$ 中,所以当点 $P$ 和点 $C$ 重合时不仅 $dis(C,P)=0$ 最小,而且 $dis(A,P)+dis(B,P)$ 最小
所以取中间的点C是最优的方案。
对于4个点时:
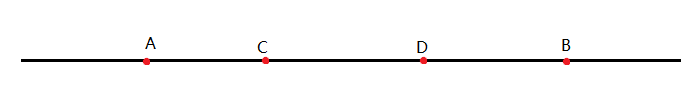
同样的思路:
设中间的点为 $C,D$,旁边的为 $A,B$
如果能满足在 $A,B$ 中间能找到一个点 $P$ 使得 $P$ 到 $C,D$ 的距离之和最小
那么 $P$ 就是最优方案(因为已经满足 $P$ 到 $A,B$ 的距离之和最小了...)
由前面可知,当 $P$ 在 $C,D$ 中间时 $P$ 到 $C,D$ 的距离之和最小,并且因为 $C,D$ 又在 $A,B$ 中间
所以当 $P$在 $C,D$ 中间时,$P$ 到各点的距离最小。
那么对于多个点时:
首先找到最外面的两个点,点 $P$ 要在它们之间
然后在找次外面的点,点 $P$ 也要在它们之间
......
一直找到只剩 $1$ 或 $2$ 个点
如果只剩一个点,那么最优方案就是 $P$ 取这个点
否则 $P$ 可以取两个点之间的任意位置
这样就可以保证方案最优
即:找到大小为中位数的点(如有两个取之间任意一点都行)
证明完毕.