可以发现图是对称的
所以我们先只考虑下半部分,不包括y=x的点
如果能算出下半部分总和为ans
那么答案就是 ans*2+1(加上y=x的方向有一个同学)
以观察者为原点,建立直角坐标系:
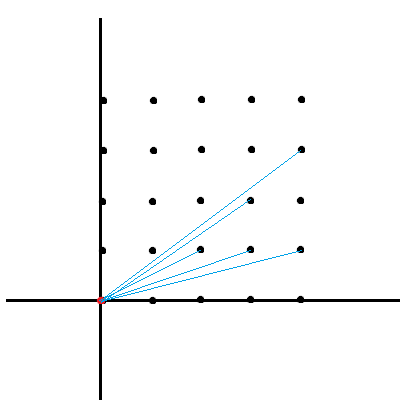
那么下半部分的视线的斜率≥0且<1,ans就是不同的斜率数量
从左到右,从下到上考虑每个点(x,y)
它能对答案有贡献当且仅当 x,y,互质
因为如果 x,y 不互质,从原点看x,y的视线的斜率就是x/y= (x/gcd(x,y)) / (y/gcd(x,y))
因为点(x/gcd(x,y) , y/gcd(x,y)) 的点之前已经被考虑过了
所以从原点到(x,y)的视线的斜率也被考虑过了,所以点(x,y)没有对答案产生贡献
如果x,y互质说明这一个斜率之前还没有被其他点"使用"(十分显然)
那就是求 1~n 中每一个小于 n 数 x 的小于x的与 x 互质的数的个数
就是求 1~n 中每一个小于 n 数 x的欧拉函数和
直接线性求出所有欧拉函数值就好了:
注意特判n=1的情况,因为观察者看不到自己所以答案为0
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> using namespace std; const int N=1e5+7; int pri[N],cnt,phi[N]; bool not_pri[N]; int n,ans; void pre() { not_pri[1]=phi[1]=1; for(int i=2;i<=n;i++) { if(!not_pri[i]) { pri[++cnt]=i; phi[i]=i-1; } for(int j=1;j<=cnt;j++) { int g=i*pri[j]; if(g>n) break; not_pri[g]=1; if(!(i%pri[j])) { phi[g]=phi[i]*pri[j]; break; } phi[g]=phi[i]*phi[pri[j]]; } } } int main() { scanf("%d",&n); if(n==1) { printf("0"); return 0; }//特判 pre(); for(int i=1;i<n;i++) ans+=phi[i]; printf("%d",ans*2+1); return 0; }