托了好久的树上差分,感觉托了一个世纪
顾z大佬写的关于树上差分的文章洛谷科技,可以直接看这个,下面的还是我自己的个人理解。
差分是种思想,不管是在1维,2维还是在树上都一样的,就是在影响开始和结束的地方设置影响值进行更新,就是实现方法上的问题。
最基本的两种树上差分是点差分和,边差分。因为有些时候给出的不是点的信息,而是边的信息,而建成树的话边的信息可以,然后对于一条边的信息,我们可以把它保存在子节点上,处理上就和点差分有所不同。
首先点差分,我们要知道树上一个类似前缀和的消息,就是一个节点可以保存在它子树上的消息,类似下图的sum,就是树上关于val的前缀和。而就是先对子数进行遍历。
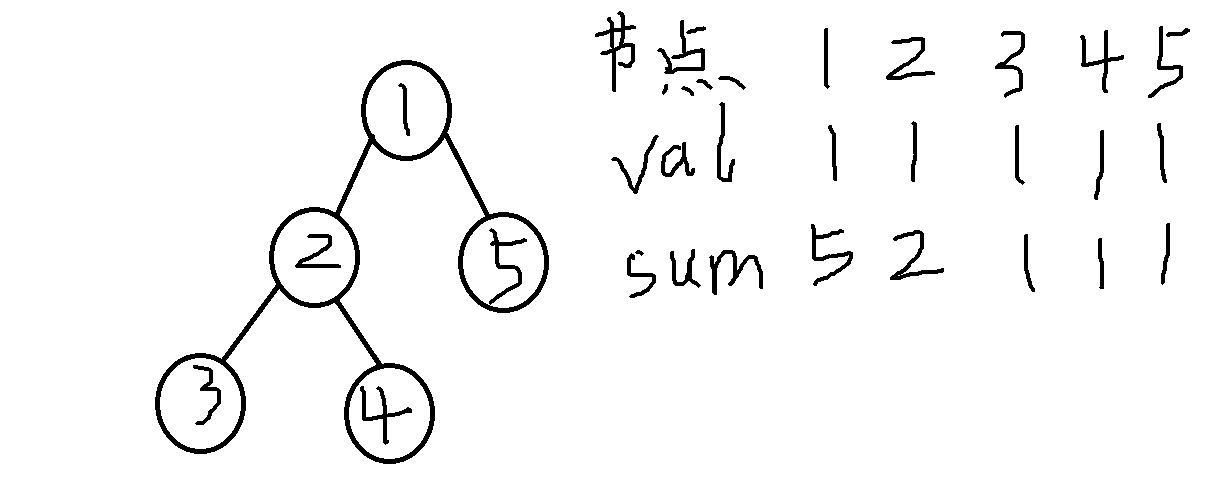
那么假设我们现在要对3到4路径上的节点的权值都+a,因为我们是先遍历的子树,那么影响的起点就是3和4,我们在3和4设置个+a,而结束的地方呢,3和4遍历后,那么2那里会有+2a的影响,而实际2应该只+a,所以2处再设置个-a,这时对上面的1还有+a的影响,1处还得再-a。
总的来说就是如果路径的起点是u,终点是v,那么dif[u]+=a,dif[v]+=a,dif[lca(u,v)]-=a,dif[fa[lca(u,v)]]-=a,其中lca(u,v)就是u和v的最近公共祖先,fa[lca(u,v)]是lca(u,v)的父节点
所以,树上差分一个很关键的点就是要懂求lca,这个在我前面的随笔我有写到,感兴趣的可以去看看。
而边差分类似,不同的在于边信息的储存在子节点,所以lca处的影响应该是0,那么就是dif[u]+=a,dif[v]+=a,dif[lca(u,v)]-=2*a
就是简单的点差分,lca上我用的树上倍增

#include<cstdio> const int N=50118,fn=20; struct Side{ int v,ne; }S[N<<1]; int sn,ans,head[N],dep[N],dif[N],fa[N][25]; void init(int n) { sn=0; for(int i=0;i<=n;i++) { head[i]=-1; dep[i]=0; dif[i]=0; for(int j=0;j<=fn;j++) fa[i][j]=0; } } void add(int u,int v) { S[sn].v=v; S[sn].ne=head[u]; head[u]=sn++; } void dfs1(int u) { for(int i=1;i<=fn;i++) { int f=fa[u][i-1]; if(!f) break; fa[u][i]=fa[f][i-1]; } for(int i=head[u];i!=-1;i=S[i].ne) { int v=S[i].v; if(v!=fa[u][0]) { fa[v][0]=u; dep[v]=dep[u]+1; dfs1(v); } } } int lca(int u,int v) { if(dep[u]<dep[v]){ int temp=u;u=v;v=temp; } int disd=dep[u]-dep[v]; for(int i=0;i<=fn;i++) if((1<<i)&disd) u=fa[u][i]; if(u==v) return u; for(int i=fn;i>=0;i--) if(fa[u][i]!=fa[v][i]) { u=fa[u][i]; v=fa[v][i]; } return fa[u][0]; } void dfs2(int u)//跑一遍深搜遍历,处理差分数组 { for(int i=head[u];i!=-1;i=S[i].ne) { int v=S[i].v; if(v!=fa[u][0]) { dfs2(v); dif[u]+=dif[v]; } } if(dif[u]>ans) ans=dif[u]; } int main() { int n,m,u,v; while(~scanf("%d%d",&n,&m)) { init(n); for(int i=1;i<n;i++) { scanf("%d%d",&u,&v); add(u,v); add(v,u); } dfs1(1); while(m--) { scanf("%d%d",&u,&v); int l=lca(u,v); dif[u]++,dif[v]++; dif[l]--,dif[fa[l][0]]--; } ans=0; dfs2(1); printf("%d ",ans); } return 0; }
也是点差分,像a1->a2->a3->a4,可以分成a1->a2,a2->a3,a3->a4三条路,而像a2在a1->a2这条路径已经计算过了,a2->a3上a2就重复计算了,而最后的a4外也不用算了,所以除了a1其他节点答案都要-1

1 #include<cstdio> 2 const int N=300118,fn=20; 3 struct Side{ 4 int v,ne; 5 }S[N<<1]; 6 int sn,ans,a[N],head[N],dep[N],dif[N],fa[N][25]; 7 void init(int n) 8 { 9 sn=0; 10 for(int i=0;i<=n;i++) 11 { 12 head[i]=-1; 13 dep[i]=0; 14 dif[i]=0; 15 for(int j=0;j<=fn;j++) 16 fa[i][j]=0; 17 } 18 } 19 void add(int u,int v) 20 { 21 S[sn].v=v; 22 S[sn].ne=head[u]; 23 head[u]=sn++; 24 } 25 void dfs1(int u) 26 { 27 for(int i=1;i<=fn;i++) 28 { 29 int f=fa[u][i-1]; 30 if(!f) 31 break; 32 fa[u][i]=fa[f][i-1]; 33 } 34 for(int i=head[u];i!=-1;i=S[i].ne) 35 { 36 int v=S[i].v; 37 if(v!=fa[u][0]) 38 { 39 fa[v][0]=u; 40 dep[v]=dep[u]+1; 41 dfs1(v); 42 } 43 } 44 } 45 int lca(int u,int v) 46 { 47 if(dep[u]<dep[v]){ 48 int temp=u;u=v;v=temp; 49 } 50 int disd=dep[u]-dep[v]; 51 for(int i=0;i<=fn;i++) 52 if((1<<i)&disd) 53 u=fa[u][i]; 54 if(u==v) 55 return u; 56 for(int i=fn;i>=0;i--) 57 if(fa[u][i]!=fa[v][i]) 58 { 59 u=fa[u][i]; 60 v=fa[v][i]; 61 } 62 return fa[u][0]; 63 } 64 void dfs2(int u) 65 { 66 for(int i=head[u];i!=-1;i=S[i].ne) 67 { 68 int v=S[i].v; 69 if(v!=fa[u][0]) 70 { 71 dfs2(v); 72 dif[u]+=dif[v]; 73 } 74 } 75 if(dif[u]>ans) 76 ans=dif[u]; 77 } 78 int main() 79 { 80 int n,m,u,v; 81 while(~scanf("%d",&n)) 82 { 83 init(n); 84 for(int i=1;i<=n;i++) 85 scanf("%d",&a[i]); 86 for(int i=1;i<n;i++) 87 { 88 scanf("%d%d",&u,&v); 89 add(u,v); 90 add(v,u); 91 } 92 dfs1(a[1]); 93 for(int i=2;i<=n;i++) 94 { 95 int l=lca(a[i-1],a[i]); 96 dif[a[i-1]]++,dif[a[i]]++; 97 dif[l]--,dif[fa[l][0]]--; 98 } 99 dfs2(a[1]); 100 for(int i=1;i<=n;i++) 101 { 102 if(i==a[1]) 103 printf("%d ",dif[i]); 104 else//除a1外,其他起点多跑了一次,而且终点最后一次也不算 105 printf("%d ",dif[i]-1); 106 } 107 } 108 return 0; 109 }
我们可以贪心地想到找到最大那条路径后,然后去掉最长边,与第二长的路径比较。但是这样很容易有反例,就是第一长的路径,第二长条的路径有一条公共的边,去掉这条边才是答案最小。那我们可以二分答案,对于当前二分的这个答案ans,那么这个ans合理的话,对于大于ans的那些路径就应该有一条公共的最长边,然后去掉它可以使得最长的路径小于等于ans。然后求lca,tarjan是O(n+m),树上倍增是nlogn,用树上倍增有一个点会超时,这时还有个小优化,就是让二分的左端点是最长的路径减去最长的边。

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 const int N=300118,fn=20; 5 struct Side{ 6 int v,w,ne; 7 }S[N<<1]; 8 struct Query{ 9 int u,v,lca,len; 10 Query(){} 11 Query(int len):len(len){} 12 bool operator<(const Query &q1) const{ 13 return len<q1.len; 14 } 15 }q[N]; 16 int n,m,sn,head[N],val[N],dep[N],dis[N],dif[N],fa[N][25]; 17 void init(int n) 18 { 19 sn=0; 20 for(int i=0;i<=n;i++) 21 { 22 head[i]=-1; 23 dep[i]=0; 24 dif[i]=0; 25 val[i]=0; 26 dis[i]=0; 27 for(int j=0;j<=fn;j++) 28 fa[i][j]=0; 29 } 30 } 31 void add(int u,int v,int w) 32 { 33 S[sn].v=v; 34 S[sn].w=w; 35 S[sn].ne=head[u]; 36 head[u]=sn++; 37 } 38 void dfs1(int u) 39 { 40 for(int i=1;i<=fn;i++) 41 { 42 int f=fa[u][i-1]; 43 if(!f) 44 break; 45 fa[u][i]=fa[f][i-1]; 46 } 47 for(int i=head[u];i!=-1;i=S[i].ne) 48 { 49 int v=S[i].v; 50 if(v!=fa[u][0]) 51 { 52 fa[v][0]=u; 53 val[v]=S[i].w;//边的权值保存在子节点上 54 dep[v]=dep[u]+1; 55 dis[v]=dis[u]+S[i].w; 56 dfs1(v); 57 } 58 } 59 } 60 int Lca(int u,int v) 61 { 62 if(dep[u]<dep[v]){ 63 int temp=u;u=v;v=temp; 64 } 65 int disd=dep[u]-dep[v]; 66 for(int i=0;i<=fn;i++) 67 if((1<<i)&disd) 68 u=fa[u][i]; 69 if(u==v) 70 return u; 71 for(int i=fn;i>=0;i--) 72 if(fa[u][i]!=fa[v][i]) 73 { 74 u=fa[u][i]; 75 v=fa[v][i]; 76 } 77 return fa[u][0]; 78 } 79 void dfs2(int u) 80 { 81 for(int i=head[u];i!=-1;i=S[i].ne) 82 { 83 int v=S[i].v; 84 if(v!=fa[u][0]) 85 { 86 dfs2(v); 87 dif[u]+=dif[v]; 88 } 89 } 90 } 91 bool check(int lim) 92 { 93 int p=upper_bound(q+1,q+1+m,Query(lim))-q;//找到第一个大于等于lim的位置 94 if(m-p+1<=0) 95 return 1; 96 for(int i=p;i<=m;i++) 97 { 98 dif[q[i].u]++,dif[q[i].v]++; 99 dif[q[i].lca]-=2; 100 }//对经过的边进行差分处理 101 dfs2(1); 102 int maxl=0; 103 for(int i=1;i<=n;i++) 104 { 105 if(dif[i]==m-p+1) 106 maxl=max(maxl,val[i]);//在都经过的边取一个最大值 107 dif[i]=0;//每次要把差分数组清空,为下次做准备 108 } 109 return q[m].len-maxl<=lim; 110 } 111 int main() 112 { 113 int u,v,w; 114 while(~scanf("%d%d",&n,&m)) 115 { 116 init(n); 117 int maxw=0; 118 for(int i=1;i<n;i++) 119 { 120 scanf("%d%d%d",&u,&v,&w); 121 maxw=max(w,maxw); 122 add(u,v,w); 123 add(v,u,w); 124 } 125 dfs1(1); 126 int l=0,r=0,ans=0; 127 for(int i=1;i<=m;i++) 128 { 129 scanf("%d%d",&q[i].u,&q[i].v); 130 q[i].lca=Lca(q[i].u,q[i].v); 131 q[i].len=dis[q[i].u]+dis[q[i].v]-2*dis[q[i].lca]; 132 l=min(l,q[i].len); 133 r=max(r,q[i].len); 134 } 135 l=r-maxw; 136 sort(q+1,q+1+m); 137 while(l<=r) 138 { 139 int mid=(l+r)>>1; 140 if(check(mid)) 141 ans=mid,r=mid-1; 142 else 143 l=mid+1; 144 } 145 printf("%d ",ans); 146 } 147 return 0; 148 }

1 #include<cstdio> 2 #include<vector> 3 #include<algorithm> 4 using namespace std; 5 typedef pair<int,int> pii; 6 const int N=300118; 7 struct Plan{ 8 int u,v,lca,len; 9 Plan(){} 10 Plan(int len):len(len){} 11 bool operator<(const Plan &p1) const{ 12 return len<p1.len; 13 } 14 }p[N]; 15 struct Side{ 16 int v,w,ne; 17 }s[N<<1],q[N<<1]; 18 int n,m,l,r,sn,qn,heads[N],headq[N],fa[N],dis[N],cost[N],vis[N],dif[N]; 19 void init() 20 { 21 l=r=0; 22 sn=qn=0; 23 for(int i=0;i<=n;i++) 24 { 25 fa[i]=i; 26 vis[i]=0; 27 dif[i]=0; 28 heads[i]=headq[i]=-1; 29 } 30 } 31 void adds(int u,int v,int w) 32 { 33 s[sn].v=v; 34 s[sn].w=w; 35 s[sn].ne=heads[u]; 36 heads[u]=sn++; 37 } 38 void addq(int u,int v,int w) 39 { 40 q[qn].v=v; 41 q[qn].w=w; 42 q[qn].ne=headq[u]; 43 headq[u]=qn++; 44 } 45 int gui(int x){ 46 return fa[x]==x ? x : fa[x]=gui(fa[x]); 47 } 48 void tarjan(int u,int f) 49 { 50 for(int i=heads[u];i!=-1;i=s[i].ne) 51 { 52 int v=s[i].v,w=s[i].w; 53 if(v!=f) 54 { 55 cost[v]=w; 56 dis[v]=dis[u]+w; 57 tarjan(v,u); 58 fa[v]=u; 59 vis[v]=1; 60 } 61 } 62 for(int i=headq[u];i!=-1;i=q[i].ne) 63 { 64 int v=q[i].v,id=q[i].w; 65 if(vis[v]) 66 { 67 p[id].u=u,p[id].v=v,p[id].lca=gui(v); 68 p[id].len=dis[u]+dis[v]-2*dis[gui(v)]; 69 r=max(r,p[id].len); 70 } 71 } 72 } 73 void dfs(int u,int f) 74 { 75 for(int i=heads[u];i!=-1;i=s[i].ne) 76 { 77 int v=s[i].v; 78 if(v!=f) 79 { 80 dfs(v,u); 81 dif[u]+=dif[v]; 82 } 83 } 84 } 85 bool check(int lim) 86 { 87 int pos=upper_bound(p+1,p+1+m,Plan(lim))-p; 88 int num=m-pos+1; 89 if(num<=0) 90 return 1; 91 for(int i=pos;i<=m;i++) 92 { 93 dif[p[i].u]++,dif[p[i].v]++; 94 dif[p[i].lca]-=2; 95 } 96 dfs(1,0); 97 int maxl=0; 98 for(int i=1;i<=n;i++) 99 { 100 if(dif[i]==num) 101 maxl=max(maxl,cost[i]); 102 dif[i]=0; 103 } 104 return p[m].len-maxl<=lim; 105 } 106 int main() 107 { 108 int u,v,w; 109 while(~scanf("%d%d",&n,&m)) 110 { 111 init(); 112 for(int i=1;i<n;i++) 113 { 114 scanf("%d%d%d",&u,&v,&w); 115 l=max(l,w); 116 adds(u,v,w); 117 adds(v,u,w); 118 } 119 for(int i=1;i<=m;i++) 120 { 121 scanf("%d%d",&u,&v); 122 addq(u,v,i); 123 addq(v,u,i); 124 } 125 tarjan(1,0); 126 sort(p+1,p+1+m); 127 int ans=0; 128 l=r-l; 129 while(l<=r) 130 { 131 int mid=(l+r)>>1; 132 if(check(mid)) 133 ans=mid,r=mid-1; 134 else 135 l=mid+1; 136 } 137 printf("%d ",ans); 138 } 139 return 0; 140 }
这题不是点差分和边差分,而是一个差分思想。对于一个玩家的路径u和v,那么有影响的肯定只是路径上的点,假如有个点x在路径上,那么它能观察到的话这个玩家的话,如果起点u在x的子树上,那么应该满足dep[x]+w[x]=dep[u],其中dep代表的是深度,如果u不在x的子树上,那么v在x的子树上,我们通过v可以得到对应这条路径的u,然后应该满足w[x]=dep[u]-dep[lca(u,v)]+dep[x]-dep[lca(u,v)],那么就是w[x]-dep[x]=dep[u]-2*dep[lca(u,v)],那么我们就是把它分成u->lca,v->lca两条路上的影响。
其中dep[x]+w[x]和w[x]-dep[x]都是定值,那么我们可以记录一个关于深度的全局差分值,这样每条路径的影响的话,如果x是a条路径的起点,那么dif[dep[x]]+=a,而如果x是一条路径的终点的话,那么dif[dep[u]-2*dep[lca(u,v)]]++,需要注意的是dep[u]-2*dep[lca(u,v)]可能是负值,而且就算它是正值它代表的是u不在x的子树上,所以要加个大正整数M作为偏移值,处理负值以及dep[u]-2*dep[lca(u,v)]可能和dep[x]相同的情况。
然后答案的统计,我们要使得做出贡献的u和v在当前x的子树上,那么就是在进入x前先记录当前的dif值,然后遍历完子树后求个差异值就是答案。
最后就是消除影响,我们可以想到因为是先遍历子树,那么最后影响结束的地方就是在lca处,那个如果x是一条路径的lca,那么我们得把这条路径贡献的影响去掉,
思路便是如此,不明白的可以看代码注释或者去看一下网上的其他题解,我之前看见个带图的讲解,不过链接忘了。实现上的话,我用tarjan卡了两天的75分,结果用树上倍增一发过了,然后发现是对于u和v相同的路径,我这个tarjan写法的lca得特判一下。

1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 using namespace std; 5 const int N=301108,M=600000; 6 struct Side{ 7 int v,ne,id; 8 }s[N<<1],q[N<<1],pathv[N],patha[N]; 9 struct Player{ 10 int u,v,lca; 11 }p[N]; 12 int sn,qn,vn,an,heads[N],headq[N],headv[N],heada[N],pathu[N]; 13 int n,m,ww[N],dep[N],ans[N],vis[N],fa[N],dif[M<<1]; 14 void init() 15 { 16 sn=qn=vn=an=dep[1]=0; 17 memset(dif,0,sizeof(dif)); 18 for(int i=0;i<=n;i++) 19 { 20 fa[i]=i; 21 ans[i]=0; 22 vis[i]=0; 23 pathu[i]=0; 24 heads[i]=headq[i]=headv[i]=heada[i]=-1; 25 } 26 } 27 void add(Side *S,int *head,int &Sn,int u,int v,int id) 28 { 29 S[Sn].v=v; 30 S[Sn].id=id; 31 S[Sn].ne=head[u]; 32 head[u]=Sn++; 33 } 34 int gui(int x){ 35 return fa[x]==x ? x : fa[x]=gui(fa[x]); 36 } 37 void tarjan(int u,int f) 38 { 39 for(int i=heads[u];~i;i=s[i].ne) 40 { 41 int v=s[i].v; 42 if(v!=f) 43 { 44 dep[v]=dep[u]+1; 45 tarjan(v,u); 46 fa[v]=u; 47 vis[v]=1; 48 } 49 } 50 for(int i=headq[u];~i;i=q[i].ne) 51 { 52 int v=q[i].v,id=q[i].id; 53 if(vis[v]) 54 p[id].lca=gui(v); 55 } 56 } 57 void dfs(int u,int f) 58 { 59 int u_a=dep[u]+ww[u],v_a=ww[u]-dep[u]+M; 60 int difu=dif[u_a],difv=dif[v_a];//先把子树外的dif记录 61 for(int i=heads[u];~i;i=s[i].ne) 62 { 63 int v=s[i].v; 64 if(v!=f) 65 dfs(v,u); 66 } 67 dif[dep[u]]+=pathu[u];//u到lca路径上的点的贡献 68 for(int i=headv[u];~i;i=pathv[i].ne) 69 { 70 int id=pathv[i].id; 71 dif[dep[p[id].u]-2*dep[p[id].lca]+M]++;//v到lca路径上的点的贡献 72 } 73 ans[u]+=dif[u_a]-difu+dif[v_a]-difv; 74 for(int i=heada[u];~i;i=patha[i].ne)//消除贡献 75 { 76 int id=patha[i].id; 77 dif[dep[p[id].u]]--; 78 dif[dep[p[id].u]-2*dep[p[id].lca]+M]--; 79 } 80 } 81 int main() 82 { 83 int u,v; 84 while(~scanf("%d%d",&n,&m)) 85 { 86 init(); 87 for(int i=1;i<n;i++) 88 { 89 scanf("%d%d",&u,&v); 90 add(s,heads,sn,u,v,0); 91 add(s,heads,sn,v,u,0); 92 } 93 for(int i=1;i<=n;i++) 94 scanf("%d",&ww[i]); 95 for(int i=1;i<=m;i++) 96 { 97 scanf("%d%d",&u,&v); 98 p[i].u=u,p[i].v=v; 99 if(u==v)//起点终点相同特判一下 100 { 101 p[i].lca=u; 102 continue; 103 } 104 add(q,headq,qn,u,v,i); 105 add(q,headq,qn,v,u,i); 106 } 107 tarjan(1,0); 108 for(int i=1;i<=m;i++) 109 { 110 pathu[p[i].u]++;//记录作为起点的路径 111 //因为起点的影响就是dep[u],所以无需建路径 112 add(pathv,headv,vn,p[i].v,p[i].u,i); 113 //记录作为终点的路径 114 add(patha,heada,an,p[i].lca,p[i].u,i); 115 //记录作为lca的路径 116 if(dep[p[i].lca]+ww[p[i].lca]==dep[p[i].u]) 117 ans[p[i].lca]--; 118 //如果u对lca有贡献,那么v时也会统计该贡献,多算了一个,去掉 119 } 120 dfs(1,0); 121 for(int i=1;i<=n;i++) 122 { 123 if(i>1) 124 putchar(' '); 125 printf("%d",ans[i]); 126 } 127 putchar(' '); 128 } 129 return 0; 130 }

1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 using namespace std; 5 const int N=301108,M=600000,fn=20; 6 struct Side{ 7 int v,ne,id; 8 }s[N<<1],q[N<<1],pathv[N],patha[N]; 9 struct Player{ 10 int u,v,lca; 11 }p[N]; 12 int sn,vn,an,heads[N],headv[N],heada[N],pathu[N]; 13 int n,m,ww[N],dep[N],ans[N],dif[M<<1],fa[N][25];; 14 void init() 15 { 16 sn=vn=an=dep[1]=0; 17 memset(dif,0,sizeof(dif)); 18 for(int i=0;i<=n;i++) 19 { 20 ans[i]=0; 21 pathu[i]=0; 22 heads[i]=headv[i]=heada[i]=-1; 23 for(int j=0;j<=fn;j++) 24 fa[i][j]=0; 25 } 26 } 27 void add(Side *S,int *head,int &Sn,int u,int v,int id) 28 { 29 S[Sn].v=v; 30 S[Sn].id=id; 31 S[Sn].ne=head[u]; 32 head[u]=Sn++; 33 } 34 void dfs1(int u) 35 { 36 for(int i=1;i<=fn;i++) 37 { 38 int f=fa[u][i-1]; 39 if(!f) 40 break; 41 fa[u][i]=fa[f][i-1]; 42 } 43 for(int i=heads[u];~i;i=s[i].ne) 44 { 45 int v=s[i].v; 46 if(v!=fa[u][0]) 47 { 48 fa[v][0]=u; 49 dep[v]=dep[u]+1; 50 dfs1(v); 51 } 52 } 53 } 54 int getlca(int u,int v) 55 { 56 if(dep[u]<dep[v]){ 57 int temp=u;u=v;v=temp; 58 } 59 int disd=dep[u]-dep[v]; 60 for(int i=0;i<=fn;i++) 61 if((1<<i)&disd) 62 u=fa[u][i]; 63 if(u==v) 64 return u; 65 for(int i=fn;i>=0;i--) 66 if(fa[u][i]!=fa[v][i]) 67 { 68 u=fa[u][i]; 69 v=fa[v][i]; 70 } 71 return fa[u][0]; 72 } 73 void dfs(int u,int f) 74 { 75 int u_a=dep[u]+ww[u],v_a=ww[u]-dep[u]+M; 76 int difu=dif[u_a],difv=dif[v_a]; 77 for(int i=heads[u];~i;i=s[i].ne) 78 { 79 int v=s[i].v; 80 if(v!=f) 81 dfs(v,u); 82 } 83 dif[dep[u]]+=pathu[u]; 84 for(int i=headv[u];~i;i=pathv[i].ne) 85 { 86 int id=pathv[i].id; 87 dif[dep[p[id].u]-2*dep[p[id].lca]+M]++; 88 } 89 ans[u]+=dif[u_a]-difu+dif[v_a]-difv; 90 for(int i=heada[u];~i;i=patha[i].ne) 91 { 92 int id=patha[i].id; 93 dif[dep[p[id].u]]--; 94 dif[dep[p[id].u]-2*dep[p[id].lca]+M]--; 95 } 96 } 97 int main() 98 { 99 int u,v; 100 while(~scanf("%d%d",&n,&m)) 101 { 102 init(); 103 for(int i=1;i<n;i++) 104 { 105 scanf("%d%d",&u,&v); 106 add(s,heads,sn,u,v,0); 107 add(s,heads,sn,v,u,0); 108 } 109 for(int i=1;i<=n;i++) 110 scanf("%d",&ww[i]); 111 dfs1(1); 112 for(int i=1;i<=m;i++) 113 { 114 scanf("%d%d",&u,&v); 115 p[i].u=u,p[i].v=v; 116 p[i].lca=getlca(u,v); 117 pathu[p[i].u]++; 118 add(pathv,headv,vn,p[i].v,p[i].u,i); 119 add(patha,heada,an,p[i].lca,p[i].u,i); 120 if(dep[p[i].lca]+ww[p[i].lca]==dep[p[i].u]) 121 ans[p[i].lca]--; 122 } 123 dfs(1,0); 124 for(int i=1;i<=n;i++) 125 { 126 if(i>1) 127 putchar(' '); 128 printf("%d",ans[i]); 129 } 130 putchar(' '); 131 } 132 return 0; 133 }
终于把树上差分给过了一遍,接下来是补上过了一遍但没写记录的树链剖分,解决完这个,想学一手qdcxk玩腻了的主席树,啊啊啊,还有一堆题没补,一堆作业没做,好忙啊啊啊
