[NOI2008] 假面舞会

[NOI2008] 假面舞会

题目大意:有(n)个人，每个人都有一个标号，每种标号的人只能看见下一个标号的人（最后一种标号看见第一种），给定(m)个关系，求这个关系是否合法以及合法情况下最大和最小的方案数,要求方案数不能小于(3)。(n⩽10^5),$m⩽10^6 $

Solution

用染色的思想；关系构成有向图，图的样式要么是环形结构，要么是树形结构

• 考虑一条链，可以任意层数，所以如果图中只有链或树，取最长链作为(ans)

  

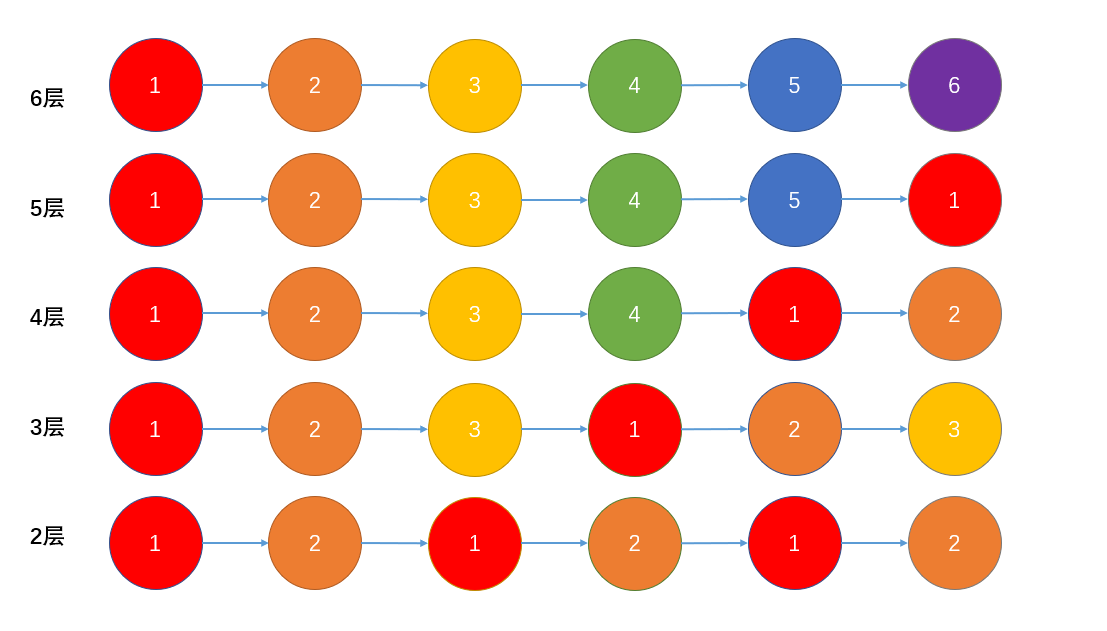
• 考虑环，因为链可以任意层数，那么有了环后，答案就是(gcd(ans, 环长)),当然在此，环指的是环状结构，有下面两种构造，建权值为(-1)的反向边可以解决第一种构造

  

  

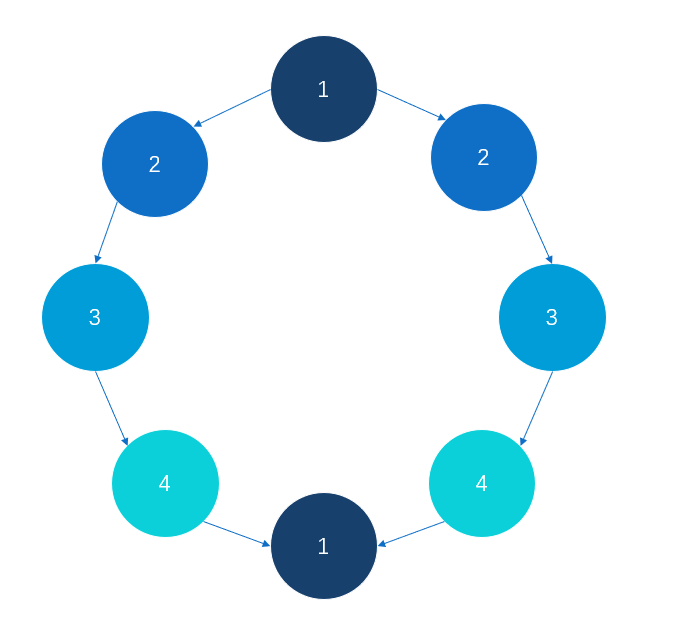
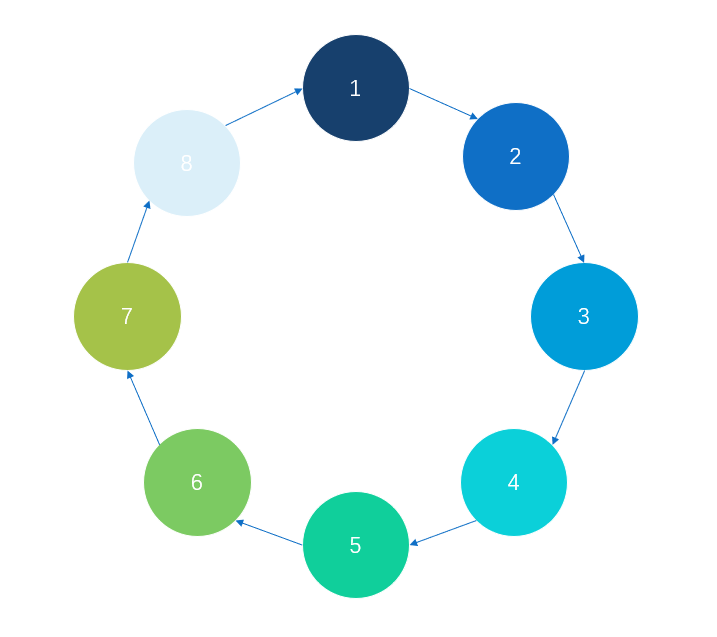
• 如果是很多环呢？

  

  

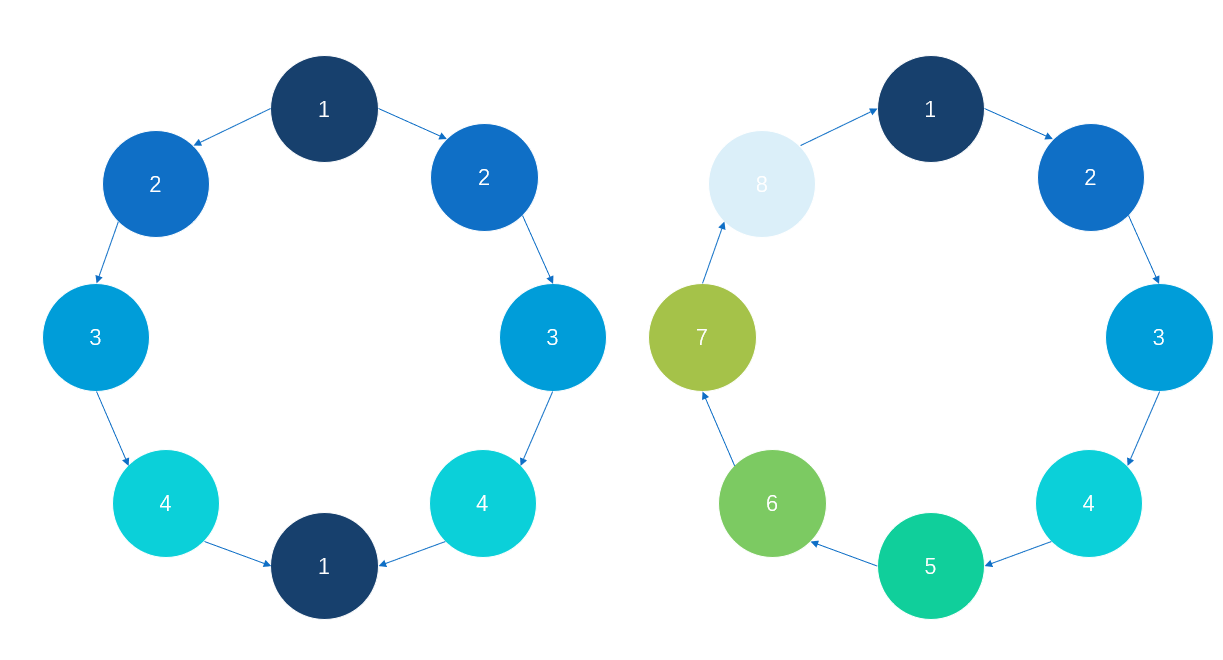
Code

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
using std::max;
using std::min;

const int N = 100005;
const int M = 1000005;

int head[N], p[N], maxx[N], minn[N], vis[N];
int cnt, tmp, ans, ans2, n, m;

struct Edge{
    int to, val, next;
}e[M << 1];

inline void addedge(int x, int y, int z){
    ++cnt;
    e[cnt].to = y;
    e[cnt].next = head[x];
    e[cnt].val = z;
    head[x] = cnt;
}

int gcd(int a, int b){
    if(b == 0)
        return a;
    else return gcd(b, a % b);
}//欧几里得算法

void dfs(int x){
    maxx[tmp] = max(maxx[tmp], p[x]), minn[tmp] = min(minn[tmp], p[x]);//记录一个联通块的链长，即标号的差 + 1
    vis[x] = true;
    for(int i = head[x], v; i; i = e[i].next){
        v = e[i].to;
        if(vis[v]){
            ans = gcd(ans, abs(p[x] + e[i].val - p[v]));//一个环,首尾标号差的绝对值//不应该在这里+1,画图可知,但是要在统计链的时候+1 
        }else{
            p[v] = p[x] + e[i].val;//标号，可能是反向边
            dfs(v);
        }
    }
}
int main(){
    scanf("%d %d", &n, &m);
    for(int i = 1, u, v; i <= m; ++i){
        scanf("%d %d", &u, &v);
        addedge(u, v, 1);
        addedge(v, u, -1);
    }
    for(int i = 1; i <= n; ++i){
        if(!vis[i]){
            minn[i] = 19260817;//初始化最小标号
            p[i] = 1;
            tmp = i;
            dfs(i);
        }
    }
    if(ans >= 3){
        for(int i = 3; i <= ans; ++i){
            if(ans % i == 0){
                ans2 = i;
                break;
            }
        }
        printf("%d %d
", ans, ans2);
        return 0;
    }else if(ans == 0){
        for(int i = 1; i <= n; ++i){
            if(maxx[i] || minn[i]){
                ans = ans + (maxx[i] - minn[i] + 1);
                
            }
        }
        if(ans >= 3){
            printf("%d 3
", ans);
            return 0;
        }else {
            printf("-1 -1
");
            return 0;
        }
    }
    /*统计答案的思路：
   如果有环了，且ans >= 3 那么我们取最小答案为它大于等于3的第一个因子
   如果有环且ans < 3, 说明不行
   如果没有环，统计最长链，ans2 = 0，如果最长链 < 3 不合法
    */
    printf("-1 -1
");
    return 0;
}