问题描述
求长度为n的排列满足(|p[i]-i|
ot =k)
n,k<=2000
解析
可以用棋盘的方法来解决这道问题。对于条件(|p[i]-i| ot =k),我们可以画出如下的棋盘图:
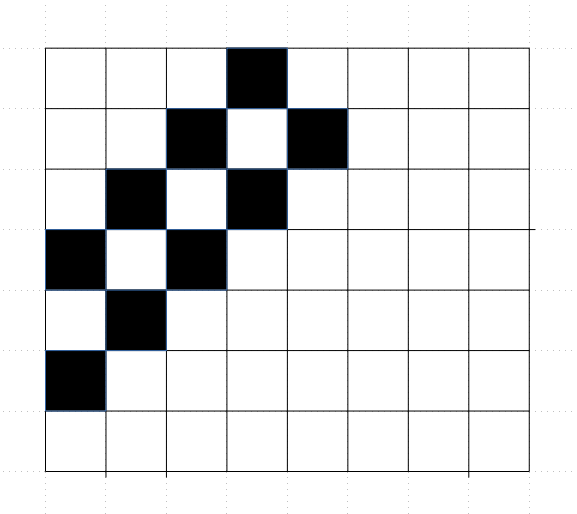
那么要求就是不能有点放在黑点上。可以用总方案数减去不合法方案数。而不合法方案数可以用容斥来计算,式子如下:
[sum(-1)^i imes F[i] imes (n-i)!
]
(F[i])表示的是有(i)个点放在黑点上的方案数。其余的点可以随便放,只要满足不同行且不同列即可,所以方案为((n-i)!) 。那么,怎么求(F [i])呢?
通过上图可以发现,如果选择了一个黑点,跟他同行同列的黑点都不能再被选择。继续观察,发现所有的矛盾关系构成几条互不干扰的链,就像下图所示:
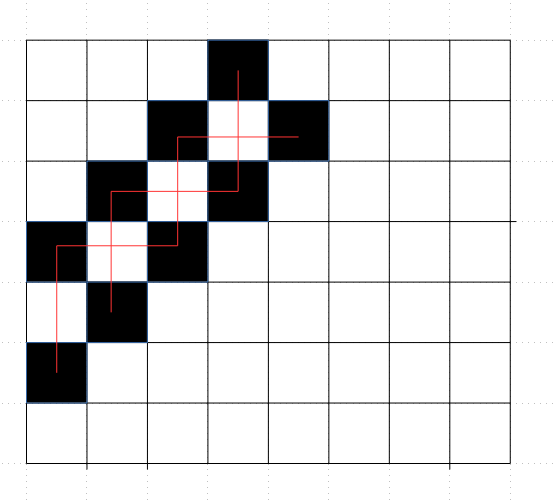
那么,在每一条链上都不能选择相邻的点。不同的链可以拼在一起,只允许相连接的地方可以相邻。这就是一个DP了。设(f[i][j][0/1])表示当前在第(i)位、选了(j)个点、第(j)个点左边相邻的点有没有选的方案数。最后有
[F[i]=f[len][i][0]+F[len][i][1]
]
(len) 表示链长之和。
代码
咕了