JZOJ 5222. 【GDOI2018模拟7.12】A（权值线段树）

JZOJ 5222. 【GDOI2018模拟7.12】A

题目

Description

Input

Output

Sample Input

3 2
2 3 1
1
1

Sample Output

2
1
1

Data Constraint

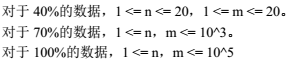
Hint

题解

这题要用到权值线段树。
首先，我们可以发现一个重要的性质：
设以$i$为左端点的逆序对个数为$s[i]$，
每个操作过的位置会使它自己和它后面$IQ$值小于他的点的$s[i]$都变为$0$。
因此，可以统计每个位置的$s[i]$最早变为$0$的时刻，即可轻松统计每个时刻的逆序对。
先把$m$次操作的位置枚举一遍，令$t[i]$为位置$i$最早被操作的时间。
一个位置$i$所对应的$s[i]$变为$0$的最早时刻，即为它或它前面比它$IQ$值大的点最早被操作的时刻。
不难想到，用建立一棵权值线段树，
将读入的$IQ$序列从左到右枚举一遍，进行如下两个操作：
1、用$t[i]$更新权值线段树上对应的表示$IQ[i]$的点（如果更小才更新）
2、在权值为$[IQ[i],max]$的区间内找到最小的数，即为该点的清零时刻$time$
自然地，把$sum[time]$加上$s[i]$。
最后$ans$先为总的逆序对个数，
每到一个时刻$i$就减去$sum[i]$，再输出。

代码

#include<cstdio>
#include<cstring>
using namespace std;
#define N 100010
int ss,a[N],p[N],s[N],h[N],t[N],f[N*5];
int last[N],to[N],next[N],len=0;
struct
{
	int id,x;
}b[N],c[N],d[N];
void gb(int l,int r)
{
	int i;
	if(l==r) return;
	else
	{
		int mid=(l+r)/2,cc,dd;
		gb(l,mid),gb(mid+1,r);
		for(i=l;i<=mid;i++) c[i-l+1]=b[i];cc=mid-l+1;
		for(i=mid+1;i<=r;i++) d[i-mid]=b[i];dd=r-mid;
		int x=1,y=1,t=1;
		while(x<=cc||y<=dd)
		{
			if(x>cc) b[l+t-1]=d[y],y++;
			else if(y>dd) b[l+t-1]=c[x],s[c[x].id]+=dd,x++;
			else if(c[x].x<=d[y].x) b[l+t-1]=c[x],s[c[x].id]+=y-1,x++; else b[l+t-1]=d[y],y++;
			t++;
		}
	}
}
void change(int k,int l,int r,int x,int y)
{
	if(l==r) 
	{
		if(y<f[k]) f[k]=y;
	}
	else
	{
		int mid=(l+r)/2;
		if(x<=mid) change(k*2,l,mid,x,y); else change(k*2+1,mid+1,r,x,y);
		if(f[k*2]<f[k*2+1]) f[k]=f[k*2]; else f[k]=f[k*2+1];
	}
}
void find(int k,int l,int r,int x,int y)
{
	if(l==x&&r==y) 
	{
		if(f[k]<ss) ss=f[k];
	}
	else
	{
		int mid=(l+r)/2;
		if(y<=mid) find(k*2,l,mid,x,y);
		else if(x>mid) find(k*2+1,mid+1,r,x,y);
		else
		{
			find(k*2,l,mid,x,mid);
			find(k*2+1,mid+1,r,mid+1,y);
		}
	}
}
void add(int x,int y)
{
	to[++len]=y;
	next[len]=last[x];
	last[x]=len;
}
int main()
{
	freopen("c.in","r",stdin);
	freopen("c.out","w",stdout);
	int n,m,i;
	scanf("%d%d",&n,&m);
	for(i=1;i<=n;i++) scanf("%d",&a[i]),b[i].id=i,b[i].x=a[i];
	gb(1,n);
	b[0].x=-1;
	for(i=1;i<=n;i++) 
	{
		if(b[i].x!=b[i-1].x) h[++h[0]]=b[i].x;
		p[b[i].id]=h[0];
	}
	memset(t,0,sizeof(t));
	memset(f,127,sizeof(f));
	for(i=1;i<=m;i++) 
	{
		scanf("%d",&c[i].x),c[i].id=i;
		if(t[c[i].x]==0) t[c[i].x]=i;
	}
	for(i=1;i<=n;i++)
	{
		if(t[i]!=0) change(1,1,h[0],p[i],t[i]);
		ss=2147483647;
		find(1,1,h[0],p[i],h[0]);
		if(ss<=m) add(ss,i);
	}
	long long ans=0;
	for(i=1;i<=n;i++) ans+=s[i];
	printf("%lld
",ans);
	for(i=1;i<=m;i++)
	{
		for(int j=last[i];j;j=next[j]) ans-=s[to[j]];
		printf("%lld
",ans);
	}
	fclose(stdin);
	fclose(stdout);
	return 0;
}