Vladik was bored on his way home and decided to play the following game. He took n cards and put them in a row in front of himself. Every card has a positive integer number not exceeding 8 written on it. He decided to find the longest subsequence of cards which satisfies the following conditions:
- the number of occurrences of each number from 1 to 8 in the subsequence doesn't differ by more then 1 from the number of occurrences of any other number. Formally, if there are ck cards with number k on them in the subsequence, than for all pairs of integers
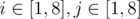the condition |ci - cj| ≤ 1 must hold. - if there is at least one card with number x on it in the subsequence, then all cards with number x in this subsequence must form a continuous segment in it (but not necessarily a continuous segment in the original sequence). For example, the subsequence [1, 1, 2, 2] satisfies this condition while the subsequence [1, 2, 2, 1] doesn't. Note that [1, 1, 2, 2] doesn't satisfy the first condition.
Please help Vladik to find the length of the longest subsequence that satisfies both conditions.
The first line contains single integer n (1 ≤ n ≤ 1000) — the number of cards in Vladik's sequence.
The second line contains the sequence of n positive integers not exceeding 8 — the description of Vladik's sequence.
Print single integer — the length of the longest subsequence of Vladik's sequence that satisfies both conditions.
3
1 1 1
1
8
8 7 6 5 4 3 2 1
8
24
1 8 1 2 8 2 3 8 3 4 8 4 5 8 5 6 8 6 7 8 7 8 8 8
17
In the first sample all the numbers written on the cards are equal, so you can't take more than one card, otherwise you'll violate the first condition.
题解：
先简单翻译一下，给一个序列，求最长的满足下面条件的子序列：
第一，相同数字连续；第二，每种数字出现次数之差不超过1
我们来考虑，由于每种数字出现都是连续的，因此一种数字一旦出现过，就不能再出现第二次。
所以我们可以用二进制来压每种数字是否出现过。
那么，每种数字出现次数的限制怎么处理？
这个东西不好说，所以我们考虑，如果有一种选择，使得每种数字都出现了至少a次，
那么一定会有其他选择，使得每种数字都出现了至少a-1次，a-2次……1次。
因此，我们就可以二分了！二分枚举每种数字至少出现的次数len，那么每种数字要么出现len次，要么出现len+1次。
对于某个len，定义状态数组f[i][j]为前i位中，数字出现状态为j时出现len+1次的数的最大种数
设tmp=max{f[i][(1<<8)-1}}，那么显然，ans=tmp*（len+1）+（8-tmp）*len
在选取新的数字时，新数字要么出现len次，要么出现len+1次，
那么状态方程也显而易见了（刷表），更新对应位置的f值即可
最后注意特判：如果二分得到len=0，那么ans=出现的数的种数
代码见下：
1 #include<cstdio> 2 #include<cstring> 3 #include<vector> 4 #include<algorithm> 5 using namespace std; 6 const int N=1010; 7 const int K=(1<<8)+10; 8 int n,a[N],f[N][K],now[10],bit[15];//now数组用来记录转移位置 9 inline int max(int a,int b){return a>b?a:b;} 10 vector<int> loc[10]; 11 inline int judge(int len) 12 { 13 for(int i=1;i<=8;i++)now[i]=0; 14 memset(f,0xaf,sizeof(f)); 15 int inf=f[0][0]; 16 f[0][0]=0; 17 for(int i=0;i<n;i++) 18 { 19 for(int j=0;j<bit[8];j++) 20 { 21 if(f[i][j]==inf)continue; 22 for(int k=0;k<8;k++) 23 { 24 if(j&bit[k])continue; 25 int pos=now[k+1]+len-1; 26 if(pos>=loc[k+1].size())continue; 27 f[loc[k+1][pos]][j|bit[k]]=max(f[loc[k+1][pos]][j|bit[k]],f[i][j]); 28 pos++; 29 if(pos>=loc[k+1].size())continue; 30 f[loc[k+1][pos]][j|bit[k]]=max(f[loc[k+1][pos]][j|bit[k]],f[i][j]+1); 31 } 32 } 33 now[a[i]]++; 34 } 35 int ans=inf; 36 for(int i=0;i<=n;i++) 37 ans=max(ans,f[i][bit[8]-1]); 38 if(ans==inf)return -1; 39 return ans*(len+1)+(8-ans)*len; 40 } 41 int main() 42 { 43 bit[0]=1;for(int i=1;i<=10;i++)bit[i]=bit[i-1]<<1; 44 scanf("%d",&n); 45 for(int i=1;i<=n;i++) 46 scanf("%d",&a[i]),loc[a[i]].push_back(i); 47 int l=0,r=n/8+1,ans=2333; 48 while(l<=r) 49 { 50 int mi=(l+r)>>1; 51 if(judge(mi)!=-1)ans=judge(mi),l=mi+1; 52 else r=mi-1; 53 } 54 if(ans==2333) 55 { 56 ans=0; 57 for(int i=1;i<=8;i++) 58 if(!loc[i].empty())ans++; 59 } 60 printf("%d",ans); 61 }