2.1 k-近邻算法概述
k-近邻算法采用测量不同特征值之间的距离方法进行分类。
优点:精度高、对异常值不敏感、无数据输入假定。
确定:计算复杂度高、空间复杂度高。
适用数据范围:数值型和标称型。
工作原理:存在一个样本数据集合,也称作训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一数据与所属分类的对应关系。输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本集中特征最相似数据(最相邻)的分类标签。一般来说,我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,通常k是不大于20的整数。最后,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
使用k-邻近算法分类爱情片和动作片。
假如有一部未看过的电影,如何确定它是爱情片还是动作片?我们可以使用kNN来解决这个问题。

首先我们需要知道这个未知电影存在多少个打斗镜头和接吻镜头,图2-1中问号位置是该未知电影出现的镜头数图形化展示,具体数字参照表2-1。

即使不知道未知电影属于哪种类型,我们也可以通过某种方式计算出来。首先计算未知电影与样本集中其他电影的距离,如表2-2所示。
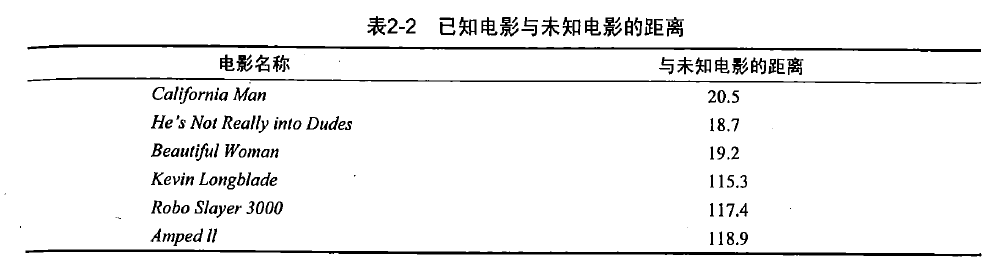
现在我们得到了样本集中所有电影与未知电影的距离,按照距离递增排序,可以找出k个距离最近的电影。假定k=3,则三个最靠近的电影依次是He's Not Really into Dudes、Beautiful Woman和California Man。k-近邻算法按照距离最近的三部电影的类型,决定未知电影的类型,而这三部电影全是爱情片,因此我们判定未知电影是爱情片。
k-邻近算法的一般流程
(1)收集数据:可以使用任何方法。
(2)准备数据:距离计算所需要的数值,最好是结构化的数据格式。
(3)分析数据:可以使用任何方法。
(4)训练算法:此步骤不适用于k-近邻算法。
(5)测试算法:计算错误率。
(6)使用算法:首先需要输入样本结构和结构化的输出结果,然后运行k-近邻算法判断输入数据分别属于哪个分类,最后应用对计算出的分类执行后续的处理。
2.1.1 准备:使用 Python 导入数据
首先,创建名为kNN.py的Python模块,所有代码放在这个文件中。
在构造完整的k-近邻算法之前,我们还需要编写一些基本的通用函数,在kNN.py文件中增加下面的代码:
from numpy import * import operator def createDataSet(): group = array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]]) labels = ['A','A','B','B'] return group, labels
在上面的代码中,我们导入了两个模块:第一个是科学计算包NumPy;第二个是运算符模块,k-近邻算法执行排序操作时将使用这个模块提供的函数。
为了方便使用createDataSet()函数,它创建数据集和标签,然后依次执行以下步骤:
1、用exit()退出Python环境在输入 pip3 install numpy
2、保存kNN.py文件,在PyChram中调出Terminal,输入以下命令导入kNN模块:
import kNN
3、为了确保输入相同的数据集,kNN模块中定义了函数createDataSet,在Terminal中输入以下命令创建变量group和labels:
group,labels = kNN.createDataSet()
4、在Terminal中输入变量的名字检验是否正确地定义变量:
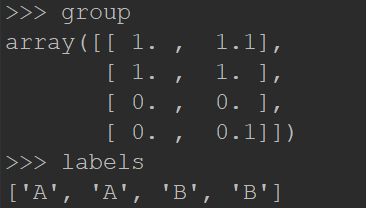
这里有4组数据,每组数据有两个我们已知的属性或者特征值。
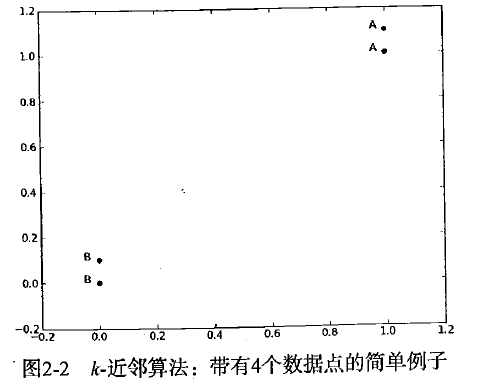
上面的group矩阵每行包含一个不同的数据,我们可以把它想象为某个日志文件中不同的测量点或者入口。为了简单地实现数据可视化,对于每个数据点我们通常只使用两个特征。
向量labels包含了每个数据点的标签信息,labels包含的元素个数等于grou矩阵行数。
这里我们将数据点(1,1.1)定义为类A,数据点(0,0.1)定义为类B。
2.1.2 从文本文件中解析数据
使用k-近邻算法将每组数据划分到某个类中,其伪代码如下:
对未知类别属性的数据集中的每个点依次执行以下操作:
(1)计算已知类别数据集中的点与当前点之间的距离;
(2)按照距离递增次序排序;
(3)选取与当前点距离最小的k个点;
(4)确定前k个点所在类别的出现频率;
(5)返回前k个点出现频率最高的类别作为当前点的预测分类。
Python函数classify0()如下:
def classify0(inX, dataSet, labels, k): # 距离计算 dataSetSize = dataSet.shape[0] diffMat = tile(inX, (dataSetSize,1)) - dataSet sqDiffMat = diffMat**2 sqDistances = sqDiffMat.sum(axis=1) distances = sqDistances**0.5 sortedDistIndicies = distances.argsort() classCount={} # 选择距离最小的k个点 for i in range(k): voteIlabel = labels[sortedDistIndicies[i]] classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1 # 排序 sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) return sortedClassCount[0][0]
classify0()函数有4个输入参数,其中:
inX是用于分类的输入向量;
dataSet是输入的训练样本;
labels是标签向量;
参数k表示用于选择最近邻居的数目;
其中,标签向量的元素数目和矩阵dataSet的行数相同。
使用欧式距离公式计算两个向量点![]() 和
和![]() 之间的距离:
之间的距离:

例如,点(0,0)与(1,2)之间的距离计算为:

如果数据集存在4个特征值,则点(1,0,0,1)与(7,6,9,4)之间的距离计算为:
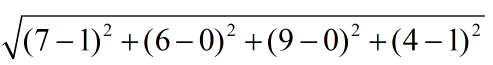
计算完所有点之间的距离后,可以对数据按照从大到小的次序排列。
然后,确定前k个距离最小元素所在的主要分类,输入k总是正整数;
最后,将classCount字典分解为元组列表,然后使用程序第二行导入运算符模块的itemgetter方法,按照第二个元素的次序对元组进行排序(此处的排序为逆序,即按照从最大到最小次序排序,最后返回发生频率最高的元素标签)。
为了预测数据所在分类,在Terminal中输入以下命令:
import kNN group,labels =kNN.createDataSet() kNN.classify0([0,0],group ,labels, 3)
输出:

2.1.3 如何测试分类器
分类器并不会得到百分百正确的结果,我们可以使用多种方法检测分类器的正确率。
此外,分类器的性能也会受到多种因素的影响,如分类器设置和数据集等。
不同的算法在不同数据集上的表现可能完全不同。
为了检测分类器的效果,我们可以使用已知答案的数据,检测分类器给出的结果是否符合预期结果。通过大量的测试数据,我们可以得到分类器的错误率——分类器给出错误结果的次数除以测试执行的总数。错误率是常用的评估方法,主要用于评估分类器在某个数据集上的执行效果。完美分类器的错误率为0,最差分类器的错误率是1.0(在这种情况下,分类器根本无法找到一个正确答案)。