Manacher算法

求回文字符串最朴素的算法就是我们枚举一个中心点，然后看看该点能够向左向右延伸多远，这样的复杂度是O(n²）

当n很大的时候，我们是无法接受的。我们必须得去优化一下算法.

如何去优化呢？

对于每一个点，我们都是以半径为0开始不断比较。

这似乎显得我们之前已经处理的信息除了记录之外没有别的用途。

能优化是因为我们还没充分地应用之前的信息。

包括求后缀数组等等，我们都是充分应用了之前的信息从而达到了高效。

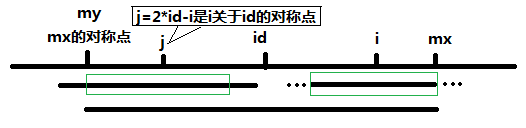
考虑到这个是回文串，我们可以假设，当前已经找到一个回文字符串，它的中心是id，半径（即回文长度的一半）是r，延伸到最右边的mx=id+i，那么区间$left[ id-r,id+r ight]$都是对称的

那么我们考察一个在这个区间的一个点 i，很显然，i 以前的点的信息我们已经算出来了，因为当前最长的回文串中心id，半径r，根据对称性，以2*id-i的点（即i关于id的对称点）为中心的回文串在区间$left[ id-r,id+r ight]$内一定会与i点相同，即以 i为中心的回文串的半径至少为$min left( mx-i,len[2ast P-i ight])$(我们已知的信息只有区间$left[ p-r,p+r ight]$是回文串，j与i关于id对称，在区间$left[ p-r,p+r ight]$内，它们的字母是关于id对称的，而以j的点为中心的回文串的最左端可能超出了my，而mx的右边并不和my的左边一样（若一样，则mx可以比当前位置更右边），但可能和i左边的mx-i的是一样的，这个我们需要单独去比较了。因此以i为中心的回文串的半径不能超过mx-i。len[i]数组记录的是以i点为中心的回文串半径），至于超过这个区间的我们只能一一去比较了。如果该回文串延伸到的最右边比之前的mx大，我们就更新id和r就可以了。复杂度为O(n).

由于回文串长度有分奇数和偶数情况，为了更好地实现，我们在每个字符旁边加上一个不会出现的特殊符号（如”#“）同时在边缘上再加上另一个符号防止越界，这样下来求得的回文串长度就是奇数了。

#include<iostream>
#include<cstring>
#include<cstdio>
#define N 100000
using namespace std;
int n,m,len[N],l,ans;
string tmp;
char qwq[N];
void insert(){
    l=0;
    qwq[0]='%';
    for (int i=0;i<tmp.size();i++){
        qwq[++l]='#';
        qwq[++l]=tmp[i];
    }
    qwq[++l]='#';
    qwq[l+1]='@';   //防止越界
}
int manacher(){
    ans=0;
    int mx=0,p=0;
    for (int i=1;i<=l;i++){
        if (mx>i) len[i]=min(mx-i,len[2*p-i]);
        else len[i]=1;
    while (qwq[i+len[i]]==qwq[i-len[i]]) len[i]++;
    if (i+len[i]>mx){    //更新p和mx
        mx=i+len[i];
        p=i;
    }
    ans=max(ans,len[i]);
    }
    return ans-1;   //减去中间那个字符
}
int main(){
    cin>>tmp;
    insert();
    printf("%d
",manacher());
    for (int i=1;i<=l;++i) cout<<len[i]<<' ';
    return 0;
}