一、DeepWalk
(2014KDD)
1、思想
随机游走+Word2vec
该算法使用随机游走(Random Walk)的方式在图中进行序列的采样.
在获得足够数量的满足一定长度的节点序列之后,就使用word2vec类似的方式,将每一个点看做单词,将点的序列看做是句子,进行训练.
Random Walk:一种可重复访问已访问节点的深度优先遍历算法。给定当前访问起始节点,从其邻居中随机采样节点作为下一个访问节点,重复此过程,直到访问序列长度满足预设条件。
Word2vec:接着利用skip-gram模型进行向量学习。
2、算法

:第一个部分是使用随机游走获得节点的序列;第二部分是使用skip-gram算法去训练得到节点的embedding向量.
3、核心代码
①构建同构网络,从网络中的每个节点开始分别进行Random Walk 采样,得到局部相关联的训练数据;
②对采样数据进行SkipGram训练,将离散的网络节点表示成向量化,最大化节点共现,使用Hierarchical Softmax来做超大规模分类的分类器
Random Walk
通过并行的方式加速路径采样,在采用多进程进行加速时,相比于开一个进程池让每次外层循环启动一个进程,我们采用固定为每个进程分配指定数量的num_walks的方式,这样可以最大限度减少进程频繁创建与销毁的时间开销。
deepwalk_walk方法对应上一节伪代码中第6行,_simulate_walks对应伪代码中第3行开始的外层循环。Parallel为多进程并行时的任务分配操作。
def deepwalk_walk(self, walk_length, start_node): walk = [start_node] while len(walk) < walk_length: cur = walk[-1] cur_nbrs = list(self.G.neighbors(cur)) if len(cur_nbrs) > 0: walk.append(random.choice(cur_nbrs)) else: break return walk def _simulate_walks(self, nodes, num_walks, walk_length,): walks = [] for _ in range(num_walks): random.shuffle(nodes) for v in nodes: walks.append(self.deepwalk_walk(alk_length=walk_length, start_node=v)) return walks results = Parallel(n_jobs=workers, verbose=verbose, )( delayed(self._simulate_walks)(nodes, num, walk_length) for num in partition_num(num_walks, workers)) walks = list(itertools.chain(*results))
Word2vec
#采用gensim中的Word2vec from gensim.models import Word2Vec w2v_model = Word2Vec(walks,sg=1,hs=1)
4、完整代码
(1)数据
wiki_edgelist:边,用来构建图
wiki_category:标签,用来评估得到的节点embedding结果

(2)模型
随机游走:
deepwalk_walk:产生当前节点的一个随机序列,从当前节点开始,从邻居节点中随机抽取walk_length个邻居产生序列。
_simulate_walks:产生图所有节点的num_walks个随机序列。
simulate_walks:并行执行_simulate_walks,并将结果合并。
from joblib import Parallel, delayed import itertools import random class RandomWalker: def __init__(self, G): self.G = G def partition_num(self,num, workers): if num % workers == 0: return [num // workers] * workers else: return [num // workers] * workers + [num % workers]
##随机游走,walk_length为游走长度,start_node为开始节点 def deepwalk_walk(self, walk_length, start_node): walk = [start_node] while len(walk) < walk_length: cur = walk[-1] cur_nbrs = list(self.G.neighbors(cur)) if len(cur_nbrs) > 0: walk.append(random.choice(cur_nbrs)) else: break return walk
def _simulate_walks(self, nodes, num_walks, walk_length, ): walks = [] for _ in range(num_walks): random.shuffle(nodes) for v in nodes: walks.append(self.deepwalk_walk(walk_length, start_node=v)) return walks
##num_walks为产生多少个随机游走序列,walk_length为游走序列长度 def simulate_walks(self, num_walks, walk_length, workers=1, verbose=0): G = self.G nodes = list(G.nodes()) results = Parallel(n_jobs=workers, verbose=verbose, )( delayed(self._simulate_walks)(nodes, num, walk_length) for num in self.partition_num(num_walks, workers)) walks = list(itertools.chain(*results)) return walks
DeepWalk(RandomWalk + Word2vec):
参数:
- graph:图
- w2v_model:word2vec模型,如skip-gram还是CBOW,滑动窗口大小等配置
- _embeddings:{节点:embedding}
- walker:构建随机游走模型类。
- sentences:调用随机游走类的函数产生图所有节点的n个随机序列。
from ..d_walker import RandomWalker from gensim.models import Word2Vec import pandas as pd class DeepWalk: def __init__(self, graph, walk_length, num_walks, workers=1): self.graph = graph self.w2v_model = None self._embeddings = {} self.walker = RandomWalker(graph) self.sentences = self.walker.simulate_walks( num_walks=num_walks, walk_length=walk_length, workers=workers, verbose=1) def train(self, embed_size=128, window_size=5, workers=3, iter=5, **kwargs): kwargs["sentences"] = self.sentences kwargs["min_count"] = kwargs.get("min_count", 0) kwargs["size"] = embed_size kwargs["sg"] = 1 # skip gram kwargs["hs"] = 1 # deepwalk use Hierarchical Softmax kwargs["workers"] = workers kwargs["window"] = window_size kwargs["iter"] = iter print("Learning embedding vectors...") model = Word2Vec(**kwargs) print("Learning embedding vectors done!") self.w2v_model = model return model def get_embeddings(self,): if self.w2v_model is None: print("model not train") return {} self._embeddings = {} for word in self.graph.nodes(): self._embeddings[word] = self.w2v_model.wv[word] return self._embeddings
(3)执行模型
from ge import DeepWalk import networkx as nx if __name__ == "__main__": G = nx.read_edgelist('../data/wiki/Wiki_edgelist.txt', create_using=nx.DiGraph(), nodetype=None, data=[('weight', int)]) model = DeepWalk(G, walk_length=10, num_walks=80, workers=1) model.train(window_size=5, iter=3) embeddings = model.get_embeddings()
二、node2vec
1、思想
随机游走改进的DeepWalk
相对于DeepWalk, node2vec的改进主要是对基于随机游走的采样策略的改进。在获得了采样方法之后,后面的学习策略就和DeepWalk一样了,这里有一点要注意的是node2vec采用了Alias算法对节点进行了采样,这是一个能将采样时间复杂度降到 的算法.
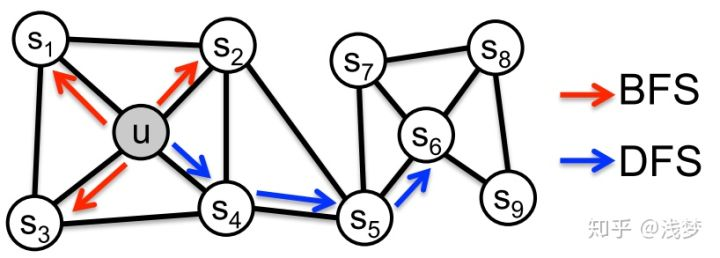
node2vec是结合了BFS和DFS的Deepwalk改进的随机游走算法。
2、随机游走策略
Deepwalk的随机游走有一个假设是所有的节点出现的概率是服从均匀分布的,但实际的情况并非如此.
(1)node2vec优化目标:


(2)node2vec随机游走:
node2vec采用的是一种有偏的随机游走。
给定当前顶点 ,访问下一个顶点
的概率为
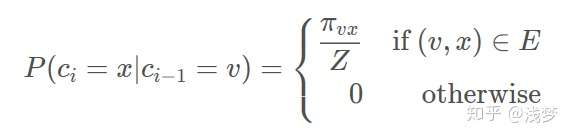
是顶点
和顶点
之间的未归一化转移概率,
是归一化常数。
node2vec引入两个超参数 和
来控制随机游走的策略,假设当前随机游走经过边
到达顶点
。一个节点转移到另外一个节点的概率不再是随机的,而是服从下面的公式:
, 转移策略为
,
是顶点
和
之间的边权。
为顶点
和顶点
之间的最短路径距离。
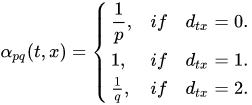
下图是对该转移策略的一个解释:
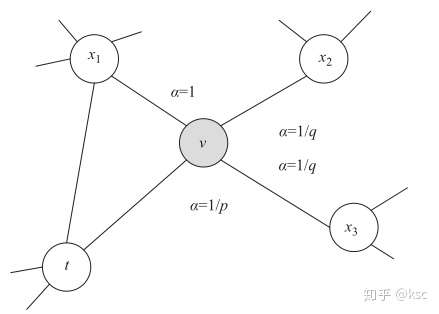
假设上一步游走的边为 , 那么对于节点
的不同邻居 , node2vec 根据
和
定义了不同的邻居的跳转概率 .
为Return parameter,因为
控制着回到原节点的概率; (d=0)
为In-out parameter,因为它控制着BFS和DFS的关系。如果
,则更倾向于BFS,如果
,则更倾向于DFS,如果
,那么node2vec其实就退化为DeepWalk算法.
(3)Alias采样
值得注意的是node2vecWalk中不再是随机抽取邻接点,而是按概率抽取,node2vec采用了Alias算法进行顶点采样。(Alias采样算法详细介绍)
问题:给定一个离散型随机变量的概率分布规律 ,希望设计一个方法能够从该概率分布中进行采样使得采样结果尽可能服从概率分布
3、算法

4、核心代码
(1)node2vecWalk
def node2vec_walk(self, walk_length, start_node): G = self.G alias_nodes = self.alias_nodes alias_edges = self.alias_edges walk = [start_node] while len(walk) < walk_length: cur = walk[-1] cur_nbrs = list(G.neighbors(cur)) if len(cur_nbrs) > 0: ###由于采样时需要考虑前面2步访问过的顶点 #当访问序列中只有1个顶点时,直接使用当前顶点和邻居顶点之间的边权作为采样依据。 if len(walk) == 1: walk.append( cur_nbrs[alias_sample(alias_nodes[cur][0], alias_nodes[cur][1])]) #当序列多余2个顶点时,使用文章提到的有偏采样 else: prev = walk[-2] edge = (prev, cur) next_node = cur_nbrs[alias_sample(alias_edges[edge][0], alias_edges[edge][1])] walk.append(next_node) else: break return walk
(2)构造采样表

alias算法的accept和alias获取:(即上面代码的alias_nodes和alias_edges)
alias_nodes:所有点的字典形式,{node:【标准化的邻居边权重列表作为概率分布而产生的accept和alias】}
alias_edges:所有边的字典形式,{edge(t,v):【x为v的邻居,所有x对应的标准化列表作为概率分布而产生的accept和alias】}
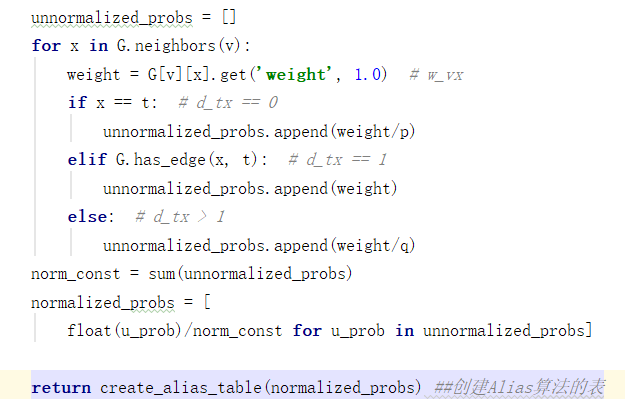
def get_alias_edge(self, t, v): G = self.G p = self.p q = self.q unnormalized_probs = [] for x in G.neighbors(v): weight = G[v][x].get('weight', 1.0)# w_vx if x == t:# d_tx == 0 unnormalized_probs.append(weight/p) elif G.has_edge(x, t):# d_tx == 1 unnormalized_probs.append(weight) else:# d_tx == 2 unnormalized_probs.append(weight/q) norm_const = sum(unnormalized_probs) normalized_probs = [float(u_prob)/norm_const for u_prob in unnormalized_probs] return create_alias_table(normalized_probs) def preprocess_transition_probs(self): G = self.G alias_nodes = {} for node in G.nodes(): unnormalized_probs = [G[node][nbr].get('weight', 1.0) for nbr in G.neighbors(node)] norm_const = sum(unnormalized_probs) normalized_probs = [float(u_prob)/norm_const for u_prob in unnormalized_probs] alias_nodes[node] = create_alias_table(normalized_probs) alias_edges = {} for edge in G.edges(): alias_edges[edge] = self.get_alias_edge(edge[0], edge[1]) self.alias_nodes = alias_nodes self.alias_edges = alias_edges return
(3)Alias算法的构造表和采样

#构造表 def create_alias_table(area_ratio): """ :param area_ratio: sum(area_ratio)=1 :return: accept,alias """ l = len(area_ratio) accept, alias = [0] * l, [0] * l small, large = [], [] area_ratio_ = np.array(area_ratio) * l for i, prob in enumerate(area_ratio_): if prob < 1.0: small.append(i) else: large.append(i) while small and large: small_idx, large_idx = small.pop(), large.pop() accept[small_idx] = area_ratio_[small_idx] alias[small_idx] = large_idx area_ratio_[large_idx] = area_ratio_[large_idx] - (1 - area_ratio_[small_idx]) if area_ratio_[large_idx] < 1.0: small.append(large_idx) else: large.append(large_idx) while large: large_idx = large.pop() accept[large_idx] = 1 while small: small_idx = small.pop() accept[small_idx] = 1 return accept, alias #采样 def alias_sample(accept, alias): """ :param accept: :param alias: :return: sample index """ N = len(accept) i = int(np.random.random()*N) r = np.random.random() if r < accept[i]: return i else: return alias[i]
5、完整代码
(1)数据+执行代码
import networkx as nx import Node2Vec if __name__ == "__main__": G=nx.read_edgelist('../data/wiki/Wiki_edgelist.txt', create_using = nx.DiGraph(), nodetype = None, data = [('weight', int)]) model=Node2Vec(G, walk_length = 10, num_walks = 80, p = 0.25, q = 4, workers = 1) model.train(window_size = 5, iter = 3) embeddings=model.get_embeddings()
(2)Node2vec类(随机游走+Word2vec)
class Node2Vec: def __init__(self, graph, walk_length, num_walks, p=1.0, q=1.0, workers=1): self.graph = graph self._embeddings = {}
###采样 self.walker = RandomWalker(graph, p=p, q=q, )
###为了构造表 print("Preprocess transition probs...") self.walker.preprocess_transition_probs() self.sentences = self.walker.simulate_walks( num_walks=num_walks, walk_length=walk_length, workers=workers, verbose=1) def train(self, embed_size=128, window_size=5, workers=3, iter=5, **kwargs): kwargs["sentences"] = self.sentences kwargs["min_count"] = kwargs.get("min_count", 0) kwargs["size"] = embed_size kwargs["sg"] = 1 kwargs["hs"] = 0 # node2vec not use Hierarchical Softmax kwargs["workers"] = workers kwargs["window"] = window_size kwargs["iter"] = iter
###Word2vec print("Learning embedding vectors...") model = Word2Vec(**kwargs) print("Learning embedding vectors done!") self.w2v_model = model return model def get_embeddings(self,): if self.w2v_model is None: print("model not train") return {} self._embeddings = {} for word in self.graph.nodes(): self._embeddings[word] = self.w2v_model.wv[word] return self._embeddings
(3)序列采样策略
import itertools
import math
import random
from .alias import alias_sample, create_alias_table
from .utils import partition_num
class RandomWalker: def __init__(self, G, p=1, q=1): """ :param G: :param p: Return parameter,controls the likelihood of immediately revisiting a node in the walk. :param q: In-out parameter,allows the search to differentiate between “inward” and “outward” nodes """ self.G = G self.p = p self.q = q ####这里是DeepWalk代码,可忽略 def deepwalk_walk(self, walk_length, start_node): walk = [start_node] while len(walk) < walk_length: cur = walk[-1] cur_nbrs = list(self.G.neighbors(cur)) if len(cur_nbrs) > 0: walk.append(random.choice(cur_nbrs)) else: break return walk def node2vec_walk(self, walk_length, start_node): G = self.G alias_nodes = self.alias_nodes alias_edges = self.alias_edges walk = [start_node] while len(walk) < walk_length: cur = walk[-1] cur_nbrs = list(G.neighbors(cur)) if len(cur_nbrs) > 0: if len(walk) == 1: walk.append( cur_nbrs[alias_sample(alias_nodes[cur][0], alias_nodes[cur][1])]) else: prev = walk[-2] edge = (prev, cur) next_node = cur_nbrs[alias_sample(alias_edges[edge][0], alias_edges[edge][1])] walk.append(next_node) else: break return walk def simulate_walks(self, num_walks, walk_length, workers=1, verbose=0): G = self.G nodes = list(G.nodes()) results = Parallel(n_jobs=workers, verbose=verbose, )( delayed(self._simulate_walks)(nodes, num, walk_length) for num in partition_num(num_walks, workers)) walks = list(itertools.chain(*results)) return walks def _simulate_walks(self, nodes, num_walks, walk_length,): walks = [] for _ in range(num_walks): random.shuffle(nodes) for v in nodes: if self.p == 1 and self.q == 1: walks.append(self.deepwalk_walk( walk_length=walk_length, start_node=v)) else: walks.append(self.node2vec_walk( walk_length=walk_length, start_node=v)) return walks def get_alias_edge(self, t, v): """ compute unnormalized transition probability between nodes v and its neighbors give the previous visited node t. :param t: :param v: :return: """ G = self.G p = self.p q = self.q unnormalized_probs = [] for x in G.neighbors(v): weight = G[v][x].get('weight', 1.0) # w_vx if x == t: # d_tx == 0 unnormalized_probs.append(weight/p) elif G.has_edge(x, t): # d_tx == 1 unnormalized_probs.append(weight) else: # d_tx > 1 unnormalized_probs.append(weight/q) norm_const = sum(unnormalized_probs) normalized_probs = [ float(u_prob)/norm_const for u_prob in unnormalized_probs] return create_alias_table(normalized_probs) ##创建Alias算法的表 def preprocess_transition_probs(self): """ Preprocessing of transition probabilities for guiding the random walks. """ G = self.G alias_nodes = {} for node in G.nodes(): unnormalized_probs = [G[node][nbr].get('weight', 1.0) for nbr in G.neighbors(node)] norm_const = sum(unnormalized_probs) normalized_probs = [ float(u_prob)/norm_const for u_prob in unnormalized_probs] alias_nodes[node] = create_alias_table(normalized_probs) alias_edges = {} for edge in G.edges(): alias_edges[edge] = self.get_alias_edge(edge[0], edge[1]) self.alias_nodes = alias_nodes self.alias_edges = alias_edges return
alias.py:(alias_sample, create_alias_table)

import numpy as np def create_alias_table(area_ratio): """ :param area_ratio: sum(area_ratio)=1 :return: accept,alias """ l = len(area_ratio) accept, alias = [0] * l, [0] * l small, large = [], [] area_ratio_ = np.array(area_ratio) * l for i, prob in enumerate(area_ratio_): if prob < 1.0: small.append(i) else: large.append(i) while small and large: small_idx, large_idx = small.pop(), large.pop() accept[small_idx] = area_ratio_[small_idx] alias[small_idx] = large_idx area_ratio_[large_idx] = area_ratio_[large_idx] - (1 - area_ratio_[small_idx]) if area_ratio_[large_idx] < 1.0: small.append(large_idx) else: large.append(large_idx) while large: large_idx = large.pop() accept[large_idx] = 1 while small: small_idx = small.pop() accept[small_idx] = 1 return accept, alias def alias_sample(accept, alias): """ :param accept: :param alias: :return: sample index """ N = len(accept) i = int(np.random.random()*N) r = np.random.random() if r < accept[i]: return i else: return alias[i]
utils.py:(partition_num)

def partition_num(num, workers): if num % workers == 0: return [num//workers]*workers else: return [num//workers]*workers + [num % workers]
三、LINE
LINE论文研究了大型信息网络如何嵌入到低维向量空间的问题,应用于可视化,节点分类,和链路预测上。大多已存在的嵌入图方法并不适用于现有的包含百万个节点的信息网络。
与DeepWalk使用DFS构造邻域不同的是,LINE可以看作是一种使用BFS构造邻域的算法。此外,LINE还可以应用在(有向、无向亦或是有权重)图中(DeepWalk仅能用于无权图),且对图中顶点之间的相似度的定义不同。
应用效果:
在稀疏数据上 line的一阶比二阶要好,增加邻居到邻居的边之后对效果有所提升。边比较多的话,一阶和二阶结合比单独使用一阶和二阶效果要更好。
1、思想
问题:
大规模信息网络嵌入:给定一个大型网络 大规模信息网络嵌入的目标是把每个节点
嵌入到低维向量空间
中。如:学习一个函数
.在
空间内,节点间的一阶相似度和二阶相似度都被保留。
(1)一种新的相似度定义

- first-order proximity(一阶相似度)
1阶相似度用于描述图中成对顶点之间的局部相似度,形式化描述为若 ,
之间存在直连边,则边权
即为两个顶点的相似度,若不存在直连边,则1阶相似度为0。 如上图,6和7之间存在直连边,且边权较大,则认为两者相似且1阶相似度较高,而5和6之间不存在直连边,则两者间1阶相似度为0。
- second-order proximity
仅有1阶相似度就够了吗?显然不够,如上图,虽然5和6之间不存在直连边,但是他们有很多相同的邻居顶点(1,2,3,4),这其实也可以表明5和6是相似的,而2阶相似度就是用来描述这种关系的。 形式化定义为,令 表示顶点
与所有其他顶点间的1阶相似度,则
与
的2阶相似度可以通过
和
的相似度表示。若
与
之间不存在相同的邻居顶点,则2阶相似度为0。
(2)优化目标
- 1st-order
对于每一条无向边 ,定义顶点
和
之间的联合概率(两者相连的可能性)为:
,
为顶点
的低维向量表示。(可以看作一个内积模型,计算两个item之间的匹配程度)
同时定义经验分布 ,
为了保留一阶相似性,最小化优化目标:
是两个分布的距离,常用的衡量两个概率分布差异的指标为KL散度
![]() ,值越大差异越大,使用KL散度替换d(.,.)并忽略常数项后有
,值越大差异越大,使用KL散度替换d(.,.)并忽略常数项后有
-----------(1)
1st order 相似度只能用于无向图当中。
- 2nd-order
这里对于每个顶点维护两个embedding向量,一个是该顶点本身的表示向量,一个是该点作为其他顶点的上下文顶点时的表示向量。
对于有向边 ,定义给定顶点
条件下,产生上下文(邻居)顶点
的概率为
,其中
为上下文顶点的个数。
优化目标为 ,其中
为控制节点重要性的因子,可以通过顶点的度数或者PageRank等方法估计得到。
经验分布定义为: ,
是边
的边权,
是顶点
的出度,对于带权图,
,其中N(i)是
节点的“出”邻居(从i节点出发的邻节点)。
为了方便,设置作为顶点i的出度,
。还采用KL散度作为距离函数,使用KL距离代替d(.,.)。设置
并忽略约束(常数项),有
---------(2)
- 一阶相似度和二阶相似度结合
(3)模型优化
- Negative sampling(负采样)
由于计算2阶相似度--公式(2)时,softmax函数的分母计算需要遍历所有顶点,这是非常低效的,论文采用了负采样优化的技巧,为每条边指定的目标函数变为:
---------(3)
其中 是sigmoid函数,第一项对观察到的边进行建模,第二项对从噪声分布中绘制的负边进行建模,
是负边的个数。
论文使用 ,
是顶点
的出度。
为了(1)式的目标函数。存在一个平凡解:.其中i=1,...,|V|且k=1...,d。为了避免平凡解,我们仍然可以使用负采样方法,仅将
变成
。
我们采用了异步随机梯度算法(ASGD)来优化等式(3)。在每一步,ASGD算法取样了一小部分的边并更新了模型的参数,如果边(i,j)被取样,那么关于i节点的嵌入向量的梯度可以被计算:
- Edge Sampling
注意到我们的目标函数在log之前还有一个权重系数 ,在使用梯度下降方法优化参数时,
会直接乘在梯度上。
如果图中的边权方差很大,则很难选择一个合适的学习率。若使用较大的学习率那么对于较大的边权可能会引起梯度爆炸,较小的学习率对于较小的边权则会导致梯度过小。
对于上述问题,如果所有边权相同,那么选择一个合适的学习率会变得容易。这里采用了将带权边拆分为等权边的一种方法,假如一个权重为 的边,则拆分后为
个权重为1的边。这样可以解决学习率选择的问题,但是由于边数的增长,存储的需求也会增加。
另一种方法则是从原始的带权边中进行采样,每条边被采样的概率正比于原始图中边的权重,这样既解决了学习率的问题,又没有带来过多的存储开销。
令
从alias table取样一条边的时间O(1),优化一个负采样需要O(d(K+1))的时间,其中K是负样本的数量。因此,总体每一步骤都需要O(dK)时间。在实践中,我们发现用于优化的步骤数量与边的数量O(|E|)成比例。因此,LINE的总的时间复杂度是O(dK|E|),与边|E|的数量呈线性关系的,且不依赖于顶点数量|V|。这种边取样方法在不影响效率的情况下提升了随机梯度下降的有效性。
(4)其他问题
- 低度数顶点
问题:如何精确嵌入具有较低度数的顶点?
对于一些顶点由于其邻接点非常少会导致embedding向量的学习不充分,论文提到可以利用邻居的邻居构造样本进行学习,这里也暴露出LINE方法仅考虑一阶和二阶相似性,对高阶信息的利用不足。
由于这类顶点的邻居数量很少,所以难以得到它所对应的精确表征,尤其是严重依赖上下文的二阶相似度。一种推论是,通过增加其高阶的邻居(如邻居的邻居)来拓展这些顶点的邻居。在本论文中,我们仅讨论增加二级邻居。即对每个顶点,增加其邻居的邻居。顶点i和其二级邻居节点j之间的距离可以被计算为:
实际上,我们可以仅为具有较低度数的顶点i增加一个有最大相似度的顶点子集{j}。
- 新加入顶点
问题二:如何得到新顶点的表征?
对于一个新顶点i,如果已知它与已存在的顶点之间连接。我们可以根据已存在的顶点获得经验分布。为了获取新顶点的嵌入,根据目标函数(3)式和(6)式。一个直接的方法通过更新新顶点的嵌入并保持已存在顶点的嵌入来最小化以下任意一个目标函数:
如果新顶点和已有节点之间有可观察的连接,我们必须求助于其他信息,例如顶点的文本信息,我们将其作为未来的工作。
2、核心代码
LINE使用梯度下降的方法进行优化,直接使用tensorflow进行实现,就可以不用人工写参数更新的逻辑了。
这里的 实现中把1阶和2阶的方法融合到一起了,可以通过超参数order控制是分开优化还是联合优化,论文推荐分开优化。
损失函数与模型
首先输入就是两个顶点的编号,然后分别拿到各自对应的embedding向量,最后输出内积的结果。 真实label定义为1或者-1,通过模型输出的内积和line_loss就可以优化使用了负采样技巧的目标函数了。
def line_loss(y_true, y_pred): return -K.mean(K.log(K.sigmoid(y_true*y_pred))) def create_model(numNodes, embedding_size, order='second'): v_i = Input(shape=(1,)) v_j = Input(shape=(1,)) first_emb = Embedding(numNodes, embedding_size, name='first_emb') second_emb = Embedding(numNodes, embedding_size, name='second_emb') context_emb = Embedding(numNodes, embedding_size, name='context_emb') v_i_emb = first_emb(v_i) v_j_emb = first_emb(v_j) v_i_emb_second = second_emb(v_i) v_j_context_emb = context_emb(v_j) first = Lambda(lambda x: tf.reduce_sum( x[0]*x[1], axis=-1, keep_dims=False), name='first_order')([v_i_emb, v_j_emb]) second = Lambda(lambda x: tf.reduce_sum( x[0]*x[1], axis=-1, keep_dims=False), name='second_order')([v_i_emb_second, v_j_context_emb]) if order == 'first': output_list = [first] elif order == 'second': output_list = [second] else: output_list = [first, second] model = Model(inputs=[v_i, v_j], outputs=output_list)
顶点负采样和边采样
下面的函数功能是创建顶点负采样和边采样需要的采样表。中规中矩,主要就是做一些预处理,然后创建alias算法需要的两个表。
- 顶点负采样:
![]() :node_degree【顶点】,顶点i 的出度权重和。
:node_degree【顶点】,顶点i 的出度权重和。
![]() :power = 0.75
:power = 0.75
norm_prob:所有顶点的 di 0.75/ ∑di0.75(∑di即total_sum) ---------->(所有顶点出度权重和,进行归一化)作为alias算法的顶点出度概率分布
- 边采样:
norm_prob :所有边权重,进行归一化,作为alias算法的边概率分布。
def _gen_sampling_table(self): # create sampling table for vertex power = 0.75 numNodes = self.node_size node_degree = np.zeros(numNodes) # out degree node2idx = self.node2idx for edge in self.graph.edges(): node_degree[node2idx[edge[0]] ] += self.graph[edge[0]][edge[1]].get('weight', 1.0) total_sum = sum([math.pow(node_degree[i], power) for i in range(numNodes)]) norm_prob = [float(math.pow(node_degree[j], power)) / total_sum for j in range(numNodes)] self.node_accept, self.node_alias = create_alias_table(norm_prob) # create sampling table for edge numEdges = self.graph.number_of_edges() total_sum = sum([self.graph[edge[0]][edge[1]].get('weight', 1.0) for edge in self.graph.edges()]) norm_prob = [self.graph[edge[0]][edge[1]].get('weight', 1.0) * numEdges / total_sum for edge in self.graph.edges()] self.edge_accept, self.edge_alias = create_alias_table(norm_prob)
3、应用代码
用LINE在wiki数据集上进行节点分类任务和可视化任务。 wiki数据集包含 2,405 个网页和17,981条网页之间的链接关系,以及每个网页的所属类别。 由于1阶相似度仅能应用于无向图中,所以本例中仅使用2阶相似度。
(1)加载数据和执行代码
import LINE import networkx as nx if __name__ == "__main__": #加载图数据 G = nx.read_edgelist('../data/wiki/Wiki_edgelist.txt', create_using=nx.DiGraph(), nodetype=None, data=[('weight', int)]) #LINE模型训练 model = LINE(G, embedding_size=128, order='second') model.train(batch_size=1024, epochs=50, verbose=2) #获取图节点embedding embeddings = model.get_embeddings()
(2)LINE模型
import math import random import numpy as np #tf2的相关模块 import tensorflow as tf from tensorflow.python.keras import backend as K from tensorflow.python.keras.layers import Embedding, Input, Lambda from tensorflow.python.keras.models import Model ##alias算法的构造表和采样 from ..alias import create_alias_table, alias_sample ##辅助函数,将图节点转化成(0,1,2,……)对应的字典 def preprocess_nxgraph(graph): node2idx = {} idx2node = [] node_size = 0 for node in graph.nodes(): node2idx[node] = node_size idx2node.append(node) node_size += 1 return idx2node, node2idx ##损失函数 def line_loss(y_true, y_pred): return -K.mean(K.log(K.sigmoid(y_true*y_pred))) ##创建模型 def create_model(numNodes, embedding_size, order='second'): v_i = Input(shape=(1,)) v_j = Input(shape=(1,)) first_emb = Embedding(numNodes, embedding_size, name='first_emb') second_emb = Embedding(numNodes, embedding_size, name='second_emb') context_emb = Embedding(numNodes, embedding_size, name='context_emb') v_i_emb = first_emb(v_i) v_j_emb = first_emb(v_j) v_i_emb_second = second_emb(v_i) v_j_context_emb = context_emb(v_j) #Lambda函数,Lambda(function)(tensor) first = Lambda(lambda x: tf.reduce_sum( x[0]*x[1], axis=-1, keep_dims=False), name='first_order')([v_i_emb, v_j_emb]) second = Lambda(lambda x: tf.reduce_sum( x[0]*x[1], axis=-1, keep_dims=False), name='second_order')([v_i_emb_second, v_j_context_emb]) if order == 'first': output_list = [first] elif order == 'second': output_list = [second] else: output_list = [first, second] model = Model(inputs=[v_i, v_j], outputs=output_list) return model, {'first': first_emb, 'second': second_emb} ##LINE模型类 class LINE: def __init__(self, graph, embedding_size=8, negative_ratio=5, order='second',): """ :param graph: :param embedding_size: :param negative_ratio: :param order: 'first','second','all' """ if order not in ['first', 'second', 'all']: raise ValueError('mode must be fisrt,second,or all') self.graph = graph self.idx2node, self.node2idx = preprocess_nxgraph(graph) self.use_alias = True self.rep_size = embedding_size self.order = order self._embeddings = {} self.negative_ratio = negative_ratio self.order = order self.node_size = graph.number_of_nodes() self.edge_size = graph.number_of_edges() self.samples_per_epoch = self.edge_size*(1+negative_ratio) # 采样表,获取边和顶点的采样accept和alias self._gen_sampling_table() # 建立模型,执行create_model和batch_iter self.reset_model() def reset_training_config(self, batch_size, times): self.batch_size = batch_size self.steps_per_epoch = ( (self.samples_per_epoch - 1) // self.batch_size + 1)*times def reset_model(self, opt='adam'): self.model, self.embedding_dict = create_model( self.node_size, self.rep_size, self.order) self.model.compile(opt, line_loss) self.batch_it = self.batch_iter(self.node2idx) def _gen_sampling_table(self): # create sampling table for vertex power = 0.75 numNodes = self.node_size node_degree = np.zeros(numNodes) # out degree node2idx = self.node2idx for edge in self.graph.edges(): node_degree[node2idx[edge[0]] ] += self.graph[edge[0]][edge[1]].get('weight', 1.0) total_sum = sum([math.pow(node_degree[i], power) for i in range(numNodes)]) norm_prob = [float(math.pow(node_degree[j], power)) / total_sum for j in range(numNodes)] self.node_accept, self.node_alias = create_alias_table(norm_prob) # create sampling table for edge numEdges = self.graph.number_of_edges() total_sum = sum([self.graph[edge[0]][edge[1]].get('weight', 1.0) for edge in self.graph.edges()]) norm_prob = [self.graph[edge[0]][edge[1]].get('weight', 1.0) * numEdges / total_sum for edge in self.graph.edges()] self.edge_accept, self.edge_alias = create_alias_table(norm_prob) def batch_iter(self, node2idx): edges = [(node2idx[x[0]], node2idx[x[1]]) for x in self.graph.edges()] data_size = self.graph.number_of_edges() shuffle_indices = np.random.permutation(np.arange(data_size)) # positive or negative mod mod = 0 mod_size = 1 + self.negative_ratio h = [] t = [] sign = 0 count = 0 start_index = 0 end_index = min(start_index + self.batch_size, data_size) while True: if mod == 0: h = [] t = [] for i in range(start_index, end_index): if random.random() >= self.edge_accept[shuffle_indices[i]]: shuffle_indices[i] = self.edge_alias[shuffle_indices[i]] cur_h = edges[shuffle_indices[i]][0] cur_t = edges[shuffle_indices[i]][1] h.append(cur_h) t.append(cur_t) sign = np.ones(len(h)) else: sign = np.ones(len(h))*-1 t = [] for i in range(len(h)): t.append(alias_sample( self.node_accept, self.node_alias)) if self.order == 'all': yield ([np.array(h), np.array(t)], [sign, sign]) else: yield ([np.array(h), np.array(t)], [sign]) mod += 1 mod %= mod_size if mod == 0: start_index = end_index end_index = min(start_index + self.batch_size, data_size) if start_index >= data_size: count += 1 mod = 0 h = [] shuffle_indices = np.random.permutation(np.arange(data_size)) start_index = 0 end_index = min(start_index + self.batch_size, data_size) def get_embeddings(self,): self._embeddings = {} if self.order == 'first': embeddings = self.embedding_dict['first'].get_weights()[0] elif self.order == 'second': embeddings = self.embedding_dict['second'].get_weights()[0] else: embeddings = np.hstack((self.embedding_dict['first'].get_weights()[ 0], self.embedding_dict['second'].get_weights()[0])) idx2node = self.idx2node for i, embedding in enumerate(embeddings): self._embeddings[idx2node[i]] = embedding return self._embeddings def train(self, batch_size=1024, epochs=1, initial_epoch=0, verbose=1, times=1): self.reset_training_config(batch_size, times) hist = self.model.fit_generator(self.batch_it, epochs=epochs, initial_epoch=initial_epoch, steps_per_epoch=self.steps_per_epoch, verbose=verbose) return hist
参考:
Graph Representation Learning:图的表示学习
