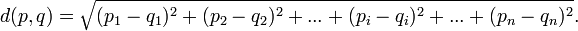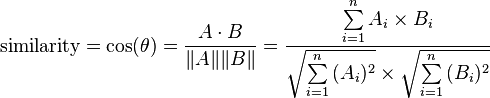zoukankan      html  css  js  c++  java

  • 海量数据分析系列一：近邻搜索的概念及其应用

    海量数据分析系列是我在学习和应用中对于一些比较常用技术的学习笔记和总结，网上有很多关于海量数据分析的宝贵资料，但很多都是英文的或专业性太强，新手学起来比较费劲。在这个系列中，将由浅入深，讲解海量数据分析里的一些概念和常用的方法，希望能作为新学习海量数据分析的同学们的参考，同时也欢迎大家指出文章中存在的错误。（文章由本人原创发表在http://www.cnblogs.com/breakinen/上，欢迎转载，转载时请务必标明出处，谢谢！）

    本文是海量数据分析系列的第一篇文章，主要介绍近邻搜索的概念，意义，方法以及在进行企业级的海量数据分析时遇到的挑战及解决思路。

    最近邻搜索（Nearest Neighbor Search）是一种被广泛应用在客户分析，文本聚类，商品推荐，模糊查询等应用中的基本的数据挖掘技术，它的目标可以简单理解为：在多维空间中，寻找离某一个数据点距离最近的点。这里的点是一个抽象概念，它可以是平面或空间里的点，也可以是一组特征（Feature）所形成的坐标点，例如用户的购买记录（对N种商品中各种商品的购买量），一篇文章（每个词在文章中出现的次数）等，而这个距离由一种特定的距离度量方法得出，例如欧几里德距离，Pearson距离，Cosine距离等。此外，K-近邻，也就是常说的KNN，是对最近邻搜索的一种扩展，用来寻找离某一个数据点距离最近的K个点。

                 image

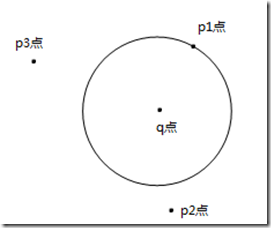
              在二维平面中对q点进行最近邻搜索，得到q点的最近邻点是p1点

    通过对海量数据进行近邻搜索，我们可以得到一系列有价值的应用，例如

    1. 商品推荐：根据某网络商城里各用户的购买记录，得到与用户A购买行为最相似的K个用户，接着就可以将这K个用户购买过而A没有购买过的商品推荐给A（这也是User-Based推荐的基本思想，当然在User-Based推荐的过程中，计算过程比上面的描述稍为复杂）
    2. 层次聚类：对各用户之间计算Pairwise Similarity，从而根据各用户间的Similarity对客户进行聚类，这样形成的聚类中，每一个聚类都有其独特的消费特征（例如喜欢购买新奇的电子产品，喜欢购买名牌护肤品等），如此以来商城就可以针对各聚类的消费特征来进行个性化营销。
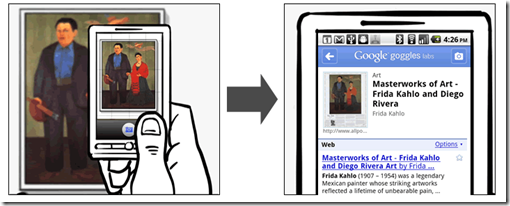
    3. 相似查询（模糊搜索）：根据客户的查询，返回和客户查询最相似的内容，例如Google去年推出的图像搜索（Google Goggles），即用户上传一张图片，Google根据这张图片找出与之最相似的图片并给出图片信息，看起来很神奇但是思想却很简单（当然实现的难度很大，涉及到很多图像特征抽取，查询优化等专业知识），同理，我们也可以进行相似股票查询、相似音乐查询、相似爱好的朋友查询等等，一般来说，只要是能用一组特征来表示的数据，都可以对其通过近邻搜索进行相似查询

      image

                                                           Google Goggles图像搜索演示

    4. 文本聚类：文本聚类是一件很神奇的事情，用户提供给计算机一系列文章，计算机自动根据每篇文章的内容来对文章进行聚类，这些类别可能包含商业、体育、教育、金融等。在这个过程中，计算机把每一篇文章看作是一个高维空间中的点，这个点的坐标是文章中各关键词及其出现个数。接着对每两个点直接进行距离测量，然后根据各篇文章之间的距离进行层次聚类（Hierarchical Clustering）或其它适合的聚类方法。

    在使用近邻搜索时，首先要考虑两个最基本，也是最重要的问题：

    如何把数据映射到高维空间中的数据点：

    一个高维空间上的点通常用一个Vector来表示其坐标，例如（1，2，1），（3，1，2），但是对于现实中的数据，怎样将其映射到空间里的一个点呢？下面我将举几个例子：

    • 描述型数据：例如一种汽车，它有四个车门，自动档，可载5人，黑色，则可以表示为 （4，1，5，1），其中第二位代表换挡方式，例如0代表手动，1代表自动，第四位代表颜色，例如1代表黑色，0代表白色，2代表蓝色等，或者，我们也可以将这个汽车的数据表示成由0，1组成的向量，例如（0，0，0，1，0，1，0，0，0，0，1，0，1，0），其中前四位代表车门数，第5、6位代表换挡方式，第7-11位代表可载入数，第12-14位代表颜色。这两种表示方式各有各的优缺点，在具体进行分析时，需要根据数据的复杂程度和距离度量的选择来决定使用数值型的坐标还是boolean型的坐标来表示数据
    • 购买记录数据：对于购买记录数据，通常把每一种商品作为一个维度，假设有四种商品 - ｛打印机，显示器，订书机，扫描仪｝，将他们作为坐标点的4个维度，如果用户有购买过某种产品，则相对应维度的数值为1，否则为0。例如：A用户购买了显示器和扫描仪，则它的购买记录的坐标为（0，1，0，1），同时，也可以用购买的数量作为坐标值。
    • 文本数据：对于文本数据，通常将每一个关键词作为一个维度，将这篇文本中每个关键词出现的次数作为坐标值，例如有以下几个关键词- ｛ 足球，北京，燃油，中国，上调，体育，计算机，数据 ｝组成一个8维的空间，则下面一段话“中国多个城市上调出租车燃油附加费 北京涨至3元”的内容映射到这个8维空间的坐标点后坐标为（ 0，1，1，1，1，0，0，0），当然这只是一个粗略的表示方式，在文本数据挖掘的过程中有很多技巧（例如经典的TF-IDF等）来进行文本特征的抽取
    • 时间序列数据：可以将时间作为坐标的维度，将各时间的值作为坐标的值来把时间序列数据映射到坐标。在实际应用中，为了减少坐标的维度，可以使用很多方法（例如SAX，PAA）等方法实现时间序列的近似表达
    • 图像数据：图像数据有很多种映射到坐标点的方式，例如抽取图像特征作为坐标维度，将颜色直方图映射为坐标，或者直接把图像中各像素点的颜色值映射成坐标等，对图像数据分析感兴趣的同学可以先学习一下图像特征抽取的相关内容

    距离度量方法的选择：

    距离度量的选择取决于数据坐标所代表的内容（比如，是代表文本数据还是购买记录），坐标的维度，坐标值的类型（如数值型还是0/1型），坐标值的大小，异常点的数量等，一般来说，比较常用的距离度量方法有以下几种：

    • 欧几里德距离（欧氏距离，Euclidean distance）：最常用的距离度量方式，对于N维空间中的坐标，两两坐标直接的距离计算公式为：

    　　d(p, q) = \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2+...+(p_i - q_i)^2+...+(p_n - q_n)^2}.

    其中p，q代表两个点，pi和qi代表p点和q点在i维度上的值，如果维度为2的话，欧氏距离就可以看作是平面直角坐标系中两点间的距离。欧氏距离因为计算速度快且稳定，因此得到广泛的使用。

    不过欧氏距离的缺点也很明显：1）不适合高维度的坐标点间距离的计算，例如文本数据和购买记录数据；2）受到异常值的影响较大，而且由于取了坐标值的平方和，因此加大了这种不利影响。

    在使用欧氏距离时，如果目的只是比较距离的远近而不在乎距离的具体值，例如对一个点做最近邻搜索时，可以省去最后开方的步骤，因为如果 d2(q,p1)>d2(q,p2)，那么d(q,p1)>d(q,p2)总是成立的（注意d(q,p)总是非负数）

    • 余弦相似度（Cosine Similarity）：将数据点视为向量，计算两向量间夹角的Cosine值，取值范围为[-1,1]，两组数据的夹角越小，Cosine越大，说明两组数据越相似。虽然它的值代表相似度，但是可以通过变换（例如1- similarity）使之表示两两坐标点之间的距离（相似度越高距离越小，相似性越小距离越大），注意这里的距离已经不再是普通意义上的距离（几何距离）。余弦相似度的计算公式如下：

    \text{similarity} = \cos(\theta) = {A \cdot B \over \|A\| \|B\|} = \frac{ \sum\limits_{i=1}^{n}{A_i \times B_i} }{ \sqrt{\sum\limits_{i=1}^{n}{(A_i)^2}} \times \sqrt{\sum\limits_{i=1}^{n}{(B_i)^2}} }

    余弦相似度对维度的增加不太敏感，适合对高维度数据进行分析，比如购买记录或文本数据。

    如果余弦相似度为0，即两组数据的夹角为90度，则表示两组数据没有重合值，例如两篇文章没有共同出现的关键字，两个客户没有共同购买过的产品。

    • 皮尔逊相关系数（Pearson's Correlation）：用来计算两组变量的相关性，取值范围为[-1,1]，皮尔逊相关系数为-1时，表示两组变量负相关，为1时表示两组变量正相关，如果值为0则表示两组变量不相关，虽然它是代表相关的系数，但是可以通过变换来使之表示两组变量（即两个点）之间的距离。皮尔逊相关系数的计算公式为：

    r_{xy}=\frac{\sum\limits_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{(n-1) s_x s_y} =\frac{\sum\limits_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})} {\sqrt{\sum\limits_{i=1}^n (x_i-\bar{x})^2 \sum\limits_{i=1}^n (y_i-\bar{y})^2}},

    • Jaccard相似度（JaccardSimilarity）：Jaccard相似度非常容易理解。假设有集合A和集合B，则他们的Jaccard相似度

       J(A,B) = {{|A \cap B|}\over{|A \cup B|}}.

    例如我们观察两个人的购物篮，A买了啤酒，饼干，蛋糕，B买了苹果，蛋糕，牛奶和饼干，则他们的Jaccard相似度为 Count{蛋糕，饼干}/Count{啤酒，饼干，蛋糕，苹果，牛奶} = 2/5 = 0.4，一般来说Jaccard相似度只适用于0/1型(或布尔型的数据)

    Jaccard广泛应用于高维数据的分析中，以后的文章中会详细讲解一种高速的针对高维数据的Jaccard相似度的近似算法：MinHashing

    普通的近邻搜索的方法 - 遍历

    一般来说，近邻搜索最简单的方法就是遍历，或者成为暴力搜索（Brute-Force Search），例如一个班有30名同学，根据每个人的兴趣爱好（可以多选）找出与学生A的兴趣爱好最相似的学生。在这个过程中，我们先把30名同学按照兴趣爱护映射到一个N维的空间中（N等于所有可能的兴趣爱好），比如：

    学生ID  -   足球，篮球，冰球，网球，排球，滑冰，滑雪

    A            1    0    0    1     0    0    1

    B            0    1    1    0     0    1    1

    … …

    然后，我们遍历除A以外的所有同学，计算A与这些同学的两两之间的距离（Distance(A,B),Distance(A,C),…），找出其中与A两两距离最小的同学，则这名同学就是与A兴趣爱好最相似的同学。

    同时，为了找到每个同学的最相似同学，可以计算这30个同学两两之间的距离（Pairwise Distance），记录在矩阵中：

         A       B       C       D       E     … 
    A    -       0.31    0.45    0.27    0.67         
    B    0.31    -       0.41    0.35    0.67   
    C    0.45    0.41    -       0.76    0.51 
    D    0.27    0.35    0.76    -       0.16 
    E    0.67    0.67    0.51    0.16    -    
    …                  

    这样，对于每个同学，只要找到矩阵中代表这个同学与其他同学距离的行（或列），找到其中最小的值，这个值所对应的列（或行）的序号就是要找的最相似的同学。

    这种方法的步骤简单清楚，可靠性高，但是因为每计算一个点的最近邻就要对集合中所有点进行一次遍历，时间代价太大，通过下面的例子不难理解在实际的海量数据分析中，暴力搜索法进行最近邻搜索是不可行的。

    在海量数据中进行近邻搜索的问题：

    借用Google News个性化推荐的场景。Google News是一个综合的新闻网站，它在全世界包含大约4500个新闻来源，据Google统计，每天的访问此网站的独立用户数就达到数百万，而这些用户中，每个用户的新闻浏览记录在0个到数百个之间。Google News可以为根据每一个用户浏览新闻的记录来向其推荐适合其偏好的新闻。

    场景看似简单，但是我们都知道，新闻的时效性很强，毫不夸张的说，在某些领域（如金融、体育）中，1个小时之前的新闻可能就已经对用户失去了吸引力，同时，几乎在每一分钟都有新的新闻进来，需要被推荐给用户。另外，由于用户需要实时获取推荐结果，因此需要在一秒钟内看到推荐页面。除去因网络延迟、前端服务器生成HTML页面、浏览器对HTML进行排版的时间，留给推荐系统的时间只有几百毫秒。

    image

    假设我们用上文提到的方式 - 根据每一个用户的新闻浏览记录，得到与用户A浏览偏好最相似的K个用户，将这K个用户浏览过而A没有浏览过的新闻推荐给A。在这个过程中，最关键的一步就是根据这个用户A的浏览记录来搜索他的K近邻。而这个搜索过程必须在几百毫秒内完成！

    如果你是Google的架构师，面对这个苛刻的需求（其实对大多数基于海量数据的实时推荐系统来说，都面临着这个问题），如何实现在数百毫秒内找到用户的K近邻呢？

    我们来计算一下使用遍历，或者暴力搜索的时间：

    假设系统中有500万用户，一共有10万条候选新闻，平均每个用户有10条浏览记录，每个用户的浏览记录以稀疏向量的形式存储在内存中（因为一共有10万条候选新闻，用户浏览记录矩阵是非常稀疏的），我们使用1 - Jaccard Similarity来作为距离度量。

    经过测试，进行10 000次两两比较需要花费10ms~20ms的时间，而使用暴力搜索需要进行5 000 000次比较，按照每次比较花费10ms来计算，进行一次近邻搜索需要5 000ms也就是5秒的时间，在实时系统中，这么长的等待时间对于用户来说是难以忍受的。

    使用缓存？

    读者可能不难想到利用缓存的方式来帮助进行近邻搜索，即事先对每一位用户都进行一次最近邻搜索并将结果保存起来，等对用户进行新闻推荐时直接使用保存的结果，这样就避免了实时的近邻搜索。这确实是一个好办法，但是仍然不能满足实时新闻推荐的需求，因为：

      • 对每一个用户都进行一次近邻搜索需要进行（5 000 000*5 000 000/2）次比较，需要12 500 000秒，也就是3472小时，或者4个月，这显然是不可接受的。当然我们也可以在分布式平台上进行并行计算，但即使有1000个节点的集群，进行一次计算也需要近4个小时
      • 新闻更新的速度很快，几乎每一分钟都有新的新闻进入系统。同时，每一分钟都有成千上万个用户浏览记录产生，如果对每一个用户的推荐只是4个小时前的新闻，对于新闻推荐系统来说，“实时”推荐已经失去了意义

    可见，对于这个庞大的新闻推荐系统来说，使用缓存并不能解决用遍历来进行近邻搜索的速度问题。

    针对海量数据加速近邻搜索的思路：

    有很多方法可以加快针对海量数据的近邻搜索速度，个人总结出以下几种思路：（假设现在我们要选出A点的K-近邻点）

    1. 减少两两比较过程的时间：使用算法优化或数据结构优化来加快距离计算的速度（对高维数据进行距离计算的速度一般来说比较慢），或者使用快速的算法来求距离的近似值，例如，使用MinHash技术来求出Jaccard距离的近似值。在海量数据处理系统中，是允许存在少量距离误差的，只要这个误差不足以对结果产生较大的影响

    2. 减少两两比较的次数：

      • 不考虑不可能成为近邻的点（剪枝）：即剪去那些离A点距离比较远，不可能成为K-近邻的点，只把剩下的点作为候选点来进行距离比较，找出K-近邻
      • 只考虑最可能成为近邻的点：在进行比较前先进行一次预选，只选出那些离A点距离比较近的点作为候选点来和A点进行距离比较，找出K-近邻

    例如，在根据新闻浏览记录来进行近邻搜索时，可以先过滤掉那些和当前用户没有浏览过同一篇文章的用户，因为这些用户的浏览记录和当前用户的浏览记录做交集后，交集内的元素数一定是0，因此Jaccard 相似度一定也为0（因为公式的分母是交集中元素的个数）。或者只选出那些看过当前用户浏览记录中新闻的用户来进行近邻搜索，当然单凭这种方法并不能使近邻搜索的时间降到数百毫秒以内。

    在接下来的文章中，将从这两个思路展开，详细介绍几种针对海量数据实现实时近邻搜索的方法。

    欢迎转载，转载请注明出处： http://www.cnblogs.com/breakinen/archive/2012/03/31/bigdata_nearest_neighbor_search.html 谢谢！

    海量数据分析系列一：近邻搜索的概念及其应用
    Breakinen 2012-03-31 22:22 阅读:506 评论:0
     
     
  • 相关阅读:
    基于MFC的Media Player播放器的制作（1---播放器界面的布局）
    Codeforces 1182
    Codeforces 1169
    Codeforces 1167
    Codeforces 1166
    Codeforces 1148
    *Codeforces 1162
    Codeforces 1159
    点分治
    高斯消元*
  • 原文地址：https://www.cnblogs.com/Leo_wl/p/2428227.html
Copyright © 2011-2022 走看看