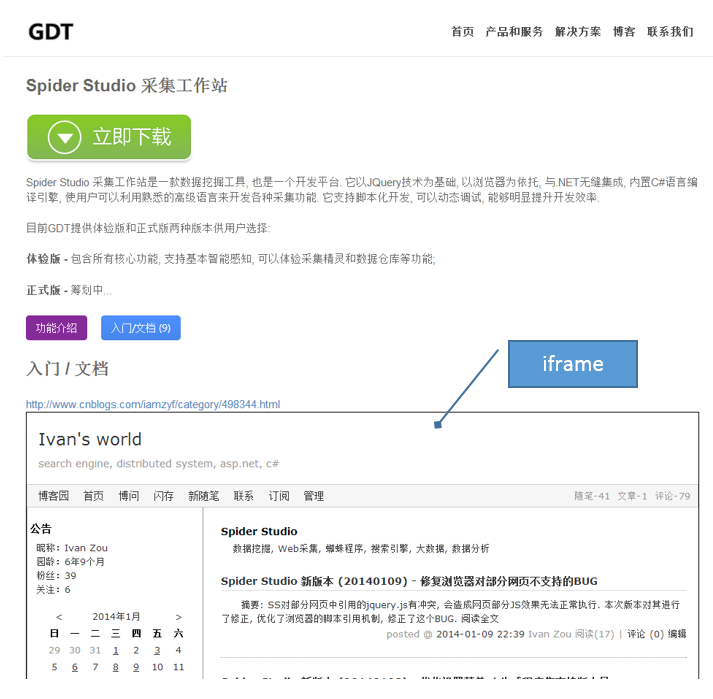
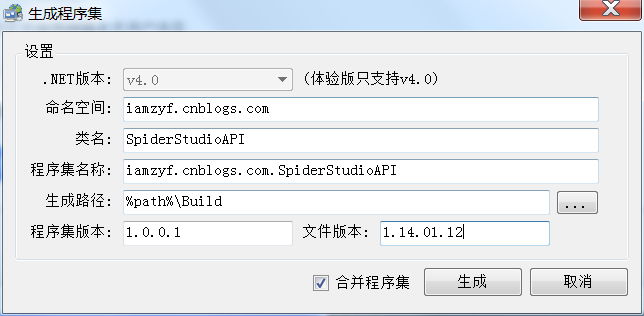
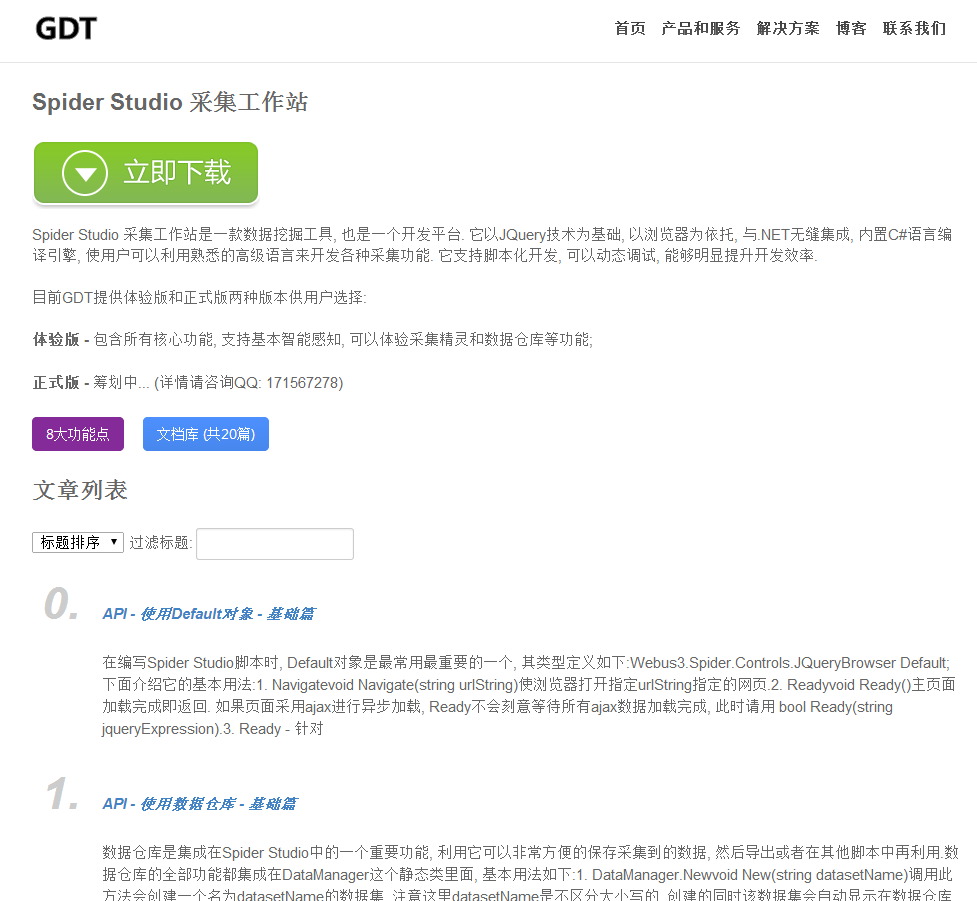
重写八皇后,最开始用双层循环,然后用递归重写,还是递归易懂,优雅
1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <string.h> 4 #include <math.h> 5 #include "stack_seq_generic.h" 6 7 #define QUEEN 4 8 9 typedef struct{ 10 int x; 11 int y; 12 } Point; 13 14 BOOL in_border(int x){ 15 if (x>=0 && x<QUEEN) { 16 return TRUE; 17 } 18 return FALSE; 19 } 20 21 BOOL can_place(SqStack *s, Point *p){ 22 Point *top = (Point *)s->top; 23 Point *base = (Point *)s->base; 24 25 if (!in_border(p->x) || !in_border(p->y)) { 26 return FALSE; 27 } 28 29 while (base < top) { 30 int x_dif = abs(p->x - base->x); 31 int y_dif = abs(p->y - base->y); 32 33 if (base->y==p->y || x_dif==y_dif) { 34 return FALSE; 35 } 36 base++; 37 } 38 return TRUE; 39 } 40 41 static int count = 0; 42 43 void print_queens(SqStack *s){ 44 Point *top = s->top; 45 Point *base = s->base; 46 47 char area[QUEEN][QUEEN] = {0}; 48 memset(area, '*', sizeof(char)*QUEEN*QUEEN); 49 50 if (top - base >= QUEEN) { 51 while (base < top) { 52 area[base->x][base->y] = '#'; 53 base++; 54 } 55 56 int i,j; 57 for (i=0; i<QUEEN; i++) { 58 for (j=0; j<QUEEN; j++) { 59 printf("%c ", area[i][j]); 60 } 61 printf(" "); 62 } 63 printf(" "); 64 65 count++; 66 } 67 68 } 69 70 void queens_recursion(SqStack *s, Point p){ 71 if (can_place(s, &p)) { 72 push(s, &p); 73 print_queens(s); 74 Point next = {p.x+1, 0}; 75 queens_recursion(s, next); 76 }else{ 77 if (stack_empty(s)) { 78 return; 79 } 80 81 if (!in_border(p.y) || !in_border(p.x)){ 82 pop(s, &p); 83 Point next = {p.x, p.y+1}; 84 queens_recursion(s, next); 85 }else{ 86 Point next = {p.x, p.y+1}; 87 queens_recursion(s, next); 88 } 89 90 } 91 } 92 93 int main(void){ 94 SqStack stack; 95 init_stack(&stack, sizeof(Point)); 96 97 //queens(&stack); 98 Point p = {0, 0}; 99 queens_recursion(&stack, p); 100 101 printf("total:%d ", count); 102 103 return 0; 104 }

 个囚犯站成一个圆圈,准备处决。首先从一个人开始,越过
个囚犯站成一个圆圈,准备处决。首先从一个人开始,越过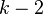 个人(因为第一个人已经被越过),并杀掉第k个人。接着,再越过
个人(因为第一个人已经被越过),并杀掉第k个人。接着,再越过 个人,并杀掉第k个人。这个过程沿着圆圈一直进行,直到最终只剩下一个人留下,这个人就可以继续活着。
个人,并杀掉第k个人。这个过程沿着圆圈一直进行,直到最终只剩下一个人留下,这个人就可以继续活着。 ,一开始要站在什么地方才能避免被处决?
,一开始要站在什么地方才能避免被处决?