Closest sum_pair

From Youtuber: CS Dojo

 

---

 

Closest sum_pair

1. Problem Statement

given two arrays and a target value, we need to find the pair value that their sum is most closest to the target value.

2. Analysis

• solution 1, brute force

  check every pair and compare the sum with the target value.(time: O(n^2))

• solution 2, traverse one array, for every element in this array, check if b = (target-ele) occurs in another array, this will cost O(n) in time; if no pair that their sum is equal to target, find the let the target1 = target-1, then repeat the former steps, if no pair, then let the target2 = target +1, then repeat the same steps; this will cost O(x*n) time, x is the difference between the result sum between the target value.

3. Solution.

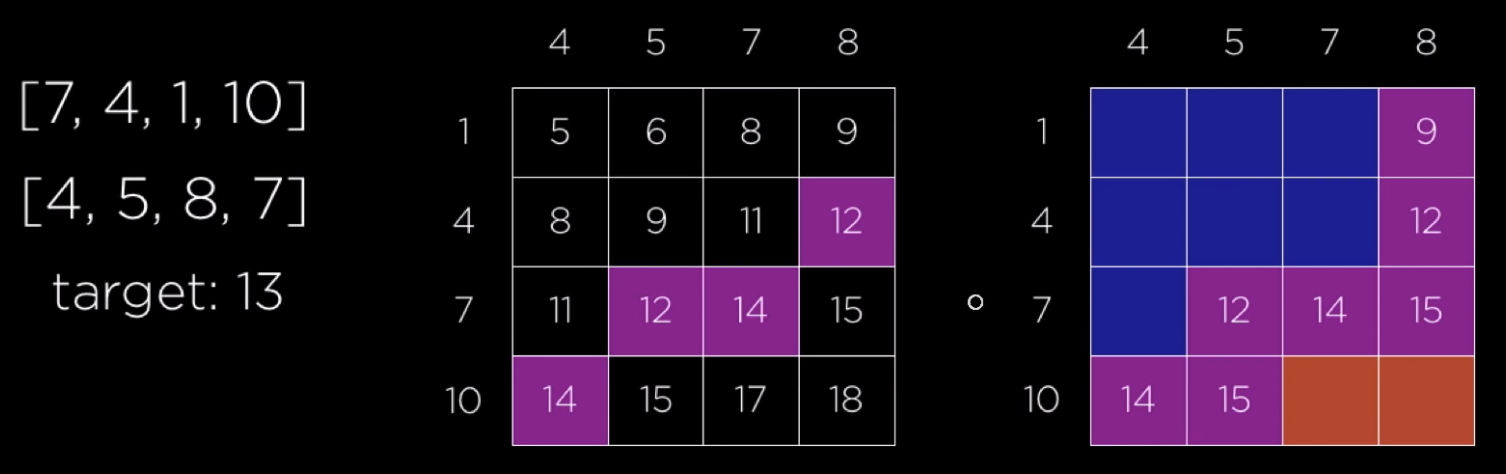
Sort the two arrays firstly, generate a matrix in which the x-axis is the sorted array a, the y-axis is the sorted array b, then use binary search to find the optimal value.  O(nlogn) time complexity and O(n) space complexity.

4. Java code

public static int[] closestSumPair(int[] a1, int[] a2, int target) {
        int[] a1Sorted = Arrays.copyOf(a1, a1.length);
        Arrays.sort(a1Sorted);
        int[] a2Sorted = Arrays.copyOf(a2, a2.length);
        Arrays.sort(a2Sorted);

        int i = 0;
        int j = a2Sorted.length - 1;
        int smallestDiff = Math.abs(a1Sorted[0] + a2Sorted[0] - target);
        int[] closestPair = {a1Sorted[0], a2Sorted[0]};

        while (i < a1Sorted.length && j >= 0 ) {
            int v1 = a1Sorted[i];
            int v2 = a2Sorted[j];
            int currentDiff = v1 + v2 - target;
            if (Math.abs(currentDiff) < smallestDiff) {
                smallestDiff = Math.abs(currentDiff);
                closestPair[0] = v1; closestPair[1] = v2;
            }

            if (currentDiff == 0) {
                return closestPair;
            }
            else if (currentDiff < 0) {
                i += 1;
            }
            else {
                j -= 1;
            }
        }

        return closestPair;
    }
}

5. Python Code

def closest_sum_pair(a1, a2, target):
    a1_sorted = sorted(a1)
    a2_sorted = sorted(a2)
    i = 0
    j = len(a2_sorted) - 1
    smallest_diff = abs(a1_sorted[0] + a2_sorted[0] - target)
    closest_pair = (a1_sorted[0], a2_sorted[0])
    while i < len(a1_sorted) and j >= 0:
        v1 = a1_sorted[i]
        v2 = a2_sorted[j]
        current_diff = v1 + v2 - target
        if abs(current_diff) < smallest_diff:
            smallest_diff = abs(current_diff)
            closest_pair = (v1, v2)

        if current_diff == 0:
            return closest_pair
        elif current_diff < 0:
            i += 1
        else:
            j -= 1
    return closest_pair