}
##$2.$贪心+二分$O(logn)$
对于上面的$n^2$代码我们会发现相当于枚举了所以转移,其中包括很多无意义的转移
***我们用$dp[len]$表示长度为$len$的最长上升子序列的末尾项的最小值***
为什么是最小值呢,我们一会说
我们还是遍历这个序列,初始默认把$dp$数组赋值为$INF$,$len=1,dp[1]=a[1]$,同时记录$len$的变化,当$a[i]>dp[len]$时就代表这个数可以接上去,于是$dp[++len]=a[i]$
***很显然,我们这么做使得$dp[i]$单调递增***
那么当$a[i]<=dp[len]$时,我们不能接上去,但我们可以考虑把$dp[i]$换掉$(dp[i]>a[i],i<=len)$,为什么要这么做呢,因为我们替换掉之后它更小了,***具有更大的更新后面的潜力***,
为了满足正确性,我们需要将大于他的最小的$dp[i]$替换掉,那么很明显我们可以用二分得出那个位置,整个程序时间复杂度$O(nlogn)$
为了方便理解,下面放几张图
数据:
11
1 2 3 100 101 4 5 6 7 8 9
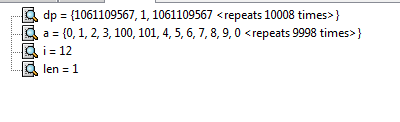
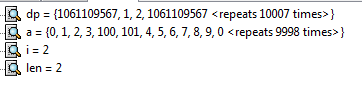
接上去
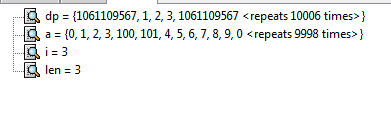
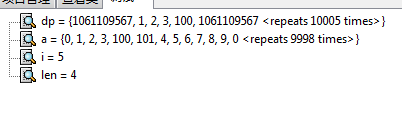
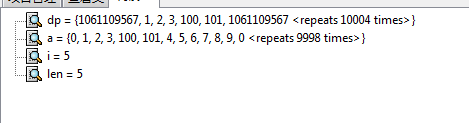
二分发现100是比4大的最小值,是替换的值,我们发现这里替换对后面的答案其实是有贡献的,当前结尾的值越小,越有可能更新后面的
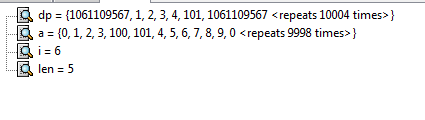
因为100已经没了,所以这次二分的位置是101

后面是索然无味的不停往后接,就不放图了,明显最长长度为9。
##$Code$
include
include
include
define maxn 10010
define re register
define inf 0x3f3f3f3f
using namespace std;
int dp[maxn],n,a[maxn],len=1;
int main()
{
scanf("%d",&n);
memset(dp,inf,sizeof(dp));
for(re int i=1;i<=n;++i)
{
scanf("%d",&a[i]);
}
dp[1]=a[1];
for(re int i=2;i<=n;++i)
{
int l=1,r=len,mid;
if(a[i]>dp[len]) dp[++len]=a[i];
else
{
while(l<=r)
{
mid=(l+r)>>1;
if(dp[mid]>a[i]) r=mid-1;
else l=mid+1;
}
// if(l<=0) l=1;
dp[l]=a[i];
}
}
printf("%d",len);
return 0;
}
##求解的个数及输出路径问题
求解的个数问题比较简单(在$O(n^2)DP$中),我们在$DP$结束后$n^2$遍历$dp$数组,如果$dp[j]=dp[i]-1&&a[j]<a[i]$,那么说明$dp[i]$可以由$dp[j]$转移而来,这时候让$ans[i]+=ans[j]即可$
最后对于每一个符合最大长度的结尾相加即可
include
include
using namespace std;
const int MAXN = 1000;
typedef pair<int, int> P;
int a[MAXN];
P dp[MAXN]; //dp[i].first表示以a[i]结尾的最长上升子序列长度,dp[i].second表示满足该长度的子序列个数
int main()
{
//输入序列
int n;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &a[i]);
}
int lis = 0;
for (int i = 0; i < n; i++) {
dp[i].first = 1;
for (int j = 0; j < i; j++) {
if (a[j] < a[i]) {
dp[i].first = max(dp[i].first, dp[j].first + 1);
}
}
//满足最长上升子序列长度的序列个数为长度为dp[i].first-1且a[j]<a[i]的个数
//即将a[i]填入长度为dp[i].first-1的序列末尾
for (int j = i - 1; j >= 0; j--) {
if (dp[j].first == dp[i].first - 1 && a[j] < a[i]) {
dp[i].second+=dp[j].second;
}
}
lis = max(lis, dp[i].first);
}
printf("%d
", lis);
int ans = 0;
for (int i = 0; i < n; i++) {
if (dp[i].first == lis) {
ans += dp[i].second;
}
}
printf("%d
", ans);
return 0;
}
输出路径:只要记录前驱,然后递归输出即可
include
using namespace std;
const int MAXN = 1000 + 10;
int n, data[MAXN];
int dp[MAXN];
int from[MAXN];
void output(int x)
{
if(!x)return;
output(from[x]);
cout<<data[x]<<" ";
//迭代输出
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)cin>>data[i];
// DP
for(int i=1;i<=n;i++)
{
dp[i]=1;
from[i]=0;
for(int j=1;j<i;j++)
if(data[j]<data[i] && dp[i]<dp[j]+1)
{
dp[i]=dp[j]+1;
from[i]=j;//逐个记录前驱
}
}
int ans=dp[1], pos=1;
for(int i=1;i<=n;i++)
if(ans<dp[i])
{
ans=dp[i];
pos=i;//由于需要递归输出
//所以要记录最长上升子序列的最后一
//个元素,来不断回溯出路径来
}
cout<<ans<<endl;
output(pos);
return 0;
}
#$LCS$问题
$LCS$问题是求两个序列最长的公共子序列,也不一定是连续的
看下面的样例
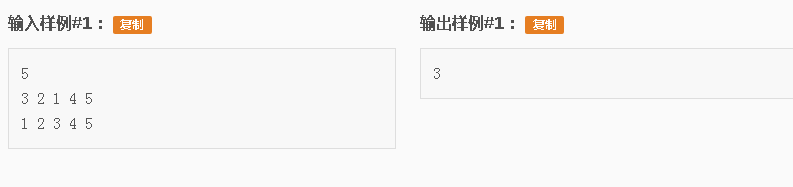
$1,4,5$这个序列在序列$A,B$中都存在,是公共子序列,而且是最长的,所以就是我们要求的最长公共子序列
##$O(nm)DP$
用$dp[i][j]$表示在第一个串的前$i$位和第二个串的前$j$位匹配的最长公共子序列
首先我们是在逐个比较,一位一位往前挪动,所以状态的继承应该为$dp[i][j]=max(dp[i-1][j],dp[i][j-1])$
如果相同的话,可以由比较的上一位继承而来,也就是$dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1)$
那么为什么不能是$dp[i][j]++$呢,这有一个反例:
$s1:a$ $s2:aa$
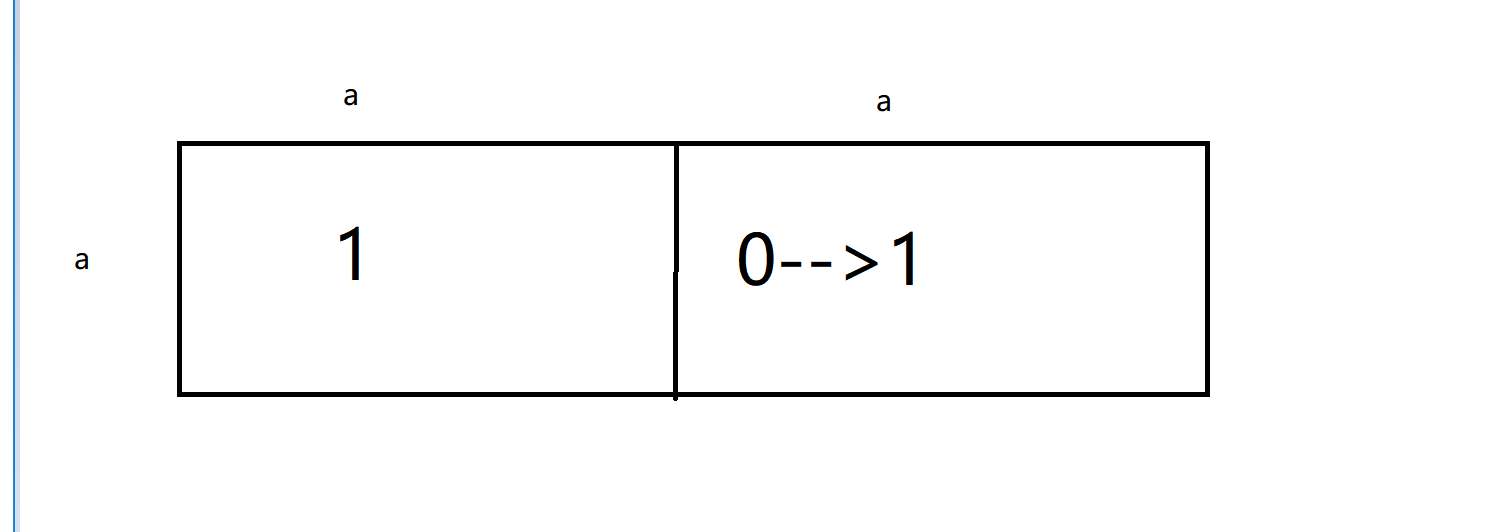
很明显$(1,2)$的正确答案应该是$1$,如果由$(1,1)$继承而来再$++$的话就会变成$2$
下面是这个过程的流程图
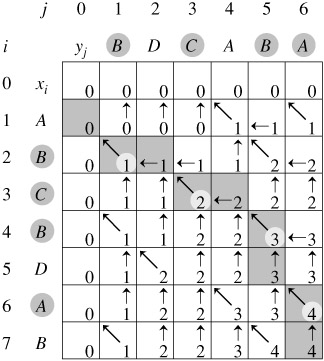
##$Code$
include
using namespace std;
int dp[1001][1001],a1[2001],a2[2001],n,m;
int main()
{
//dp[i][j]表示两个串从头开始,直到第一个串的第i位
//和第二个串的第j位最多有多少个公共子元素
cin>>n>>m;
for(int i=1;i<=n;i++)scanf("%d",&a1[i]);
for(int i=1;i<=m;i++)scanf("%d",&a2[i]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
if(a1[i]==a2[j])
dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1);
//因为更新,所以++;
}
cout<<dp[n][m];
}
##例题:$Luogu P1439$
<font size=4>
题目大意:给出$1-n$的两个排列$P1$和$P2$,求它们的最长公共子序列。
$n≤100000$
</font>
这道题用$O(nm)DP$明显不行,
我们寻找条件发现题目中说这两个序列都是$1-n$的排列,也就是说,将序列$A , B$间相同的元素连边,会形成一一对应的映射关系,我们可以用$map$数组记录这种映射关系
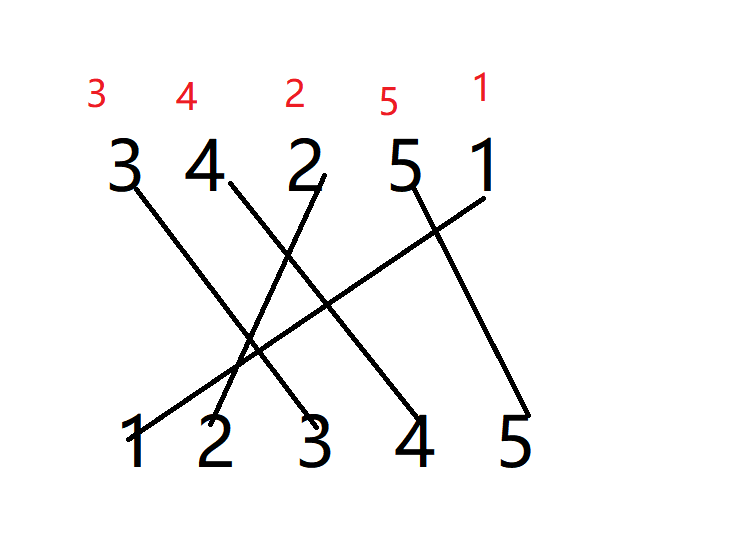
上方红字表示$map$数组
因为**最长公共子序列是按位向后比对的,所以a序列每个元素在b序列中的位置如果递增,就说明b中的这个数在a中的这个数整体位置偏后**
**换而言之,因为$a$数组的下标是单调上升的,如果$map$数组表示的映射也就是相同的数在$b$中的位置也是单调上升的,那么就一定可以构成公共子序列**
要求最长公共子序列,只需要在$map$数组中求最长上升子序列即可。复杂度$O(nlogn)$
当然这种做法仅仅适用于这种特殊题目,当不存在这种一一映射关系时,这种方法能使用。
##$Code$
include
include
include
define maxn 100001
pragma GCC optimize(3)
define re register
using namespace std;
int a[maxn],b[maxn],c[maxn],dp[maxn],n,len=1;
int main()
{
scanf("%d",&n);
for(re int i=1;i<=n;++i){scanf("%d",&a[i]);}
for(re int i=1;i<=n;++i){scanf("%d",&b[i]);c[b[i]]=i;}
memset(dp,0x3f3f3f3f,sizeof(dp));
dp[1]=c[a[1]];
for(re int i=2;i<=n;++i)
{
int l=1,r=len,mid;
if(c[a[i]]>dp[len]) dp[++len]=c[a[i]];
else
{
while(l<=r)
{
mid=(l+r)>>1;
if(dp[mid]>c[a[i]]) r=mid-1;
else l=mid+1;
}
dp[l]=c[a[i]];
}
}
printf("%d",len);
return 0;
}
</font>