题目链接
题意分析
一道不错的旋转坐标系的题
首先 由于一个点的固定曼哈顿距离围成的点形成了一个斜正方形 所以我们旋转坐标系 将其转化为正方形
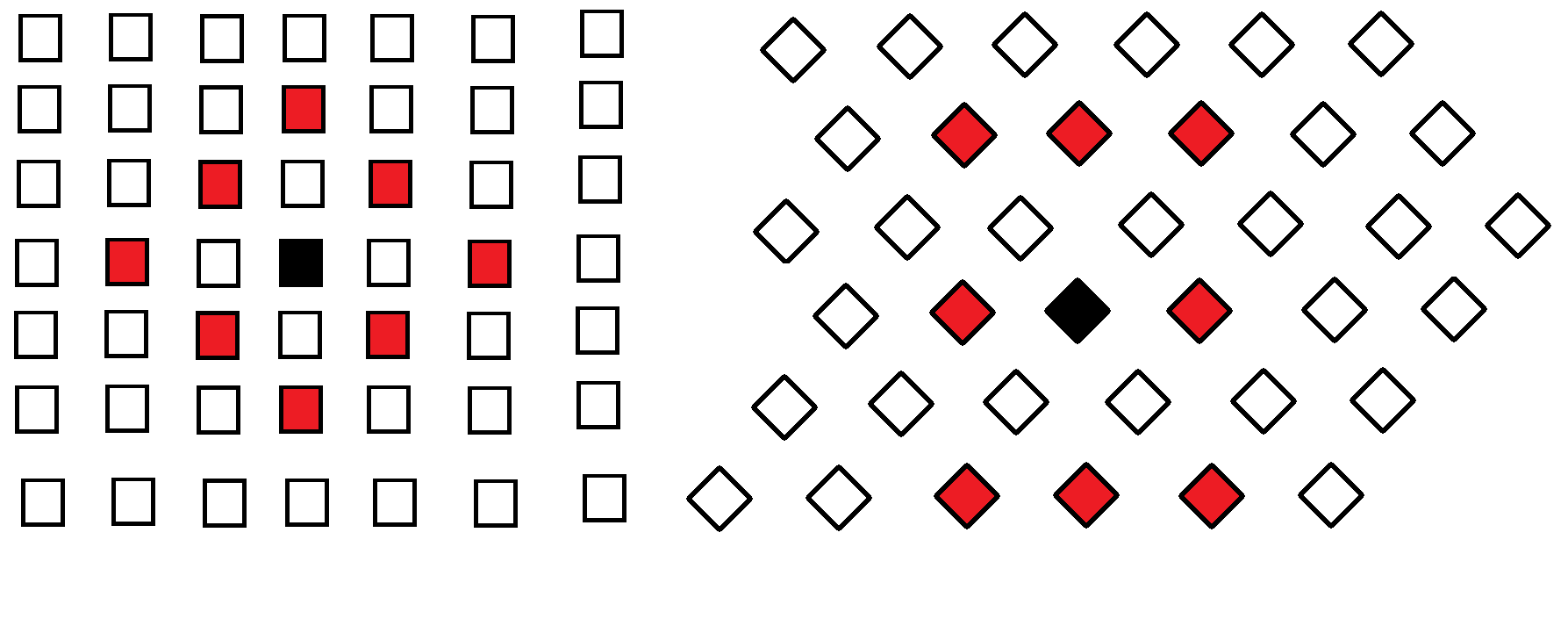
就是这样 然后我们考虑划分为若干矩形 是的每一个矩形内可以然同一种颜色 同时与ta周围的8个矩形不可以染同种颜色
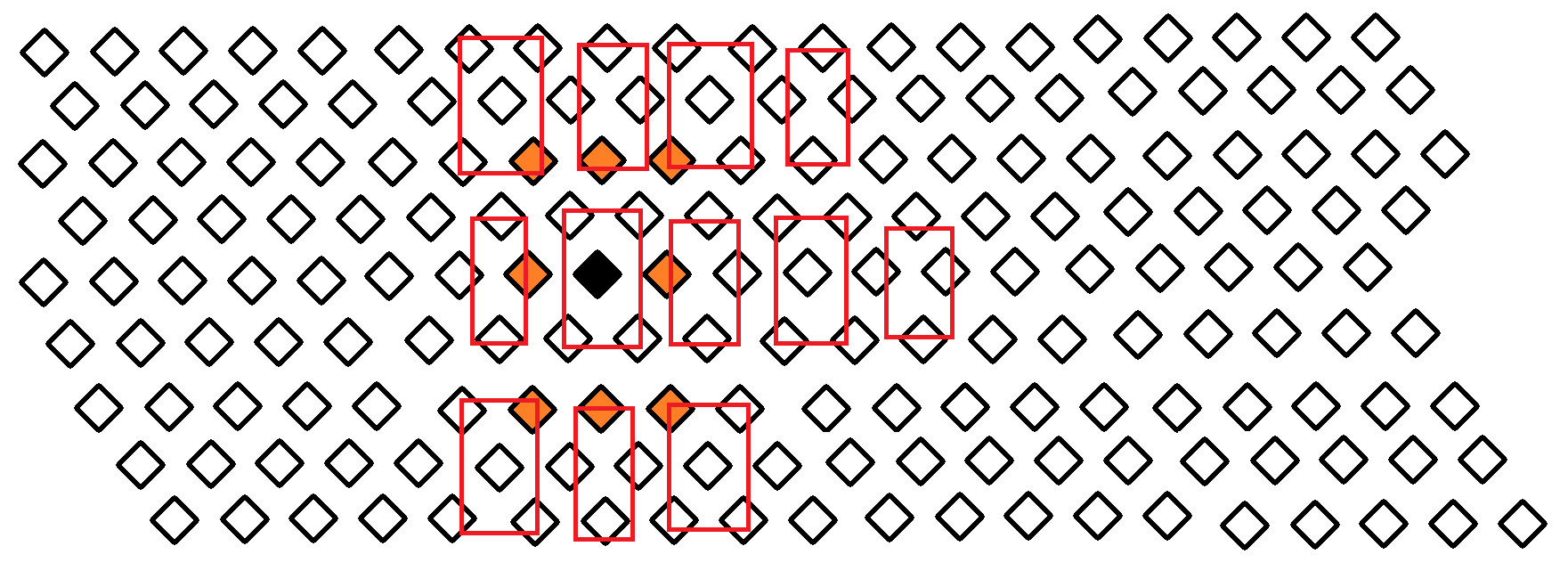
就是这样子(图画的不太好 凑活着看一下吧)
然后对于矩形的话 我们考虑按照奇偶性进行染色
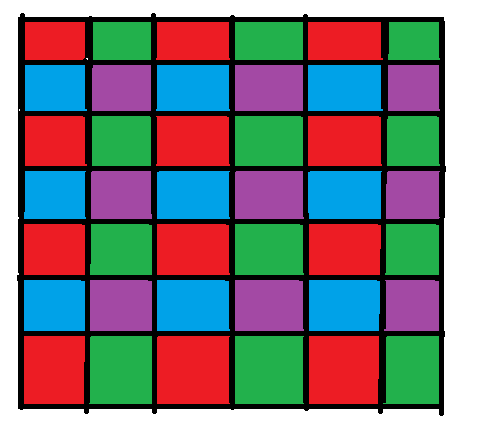
CODE:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<cmath>
using namespace std;
int n,m,d;
int num[5000][5000];
int bel[5000][5000];
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>n>>m>>d;
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
{
int x=i+j+m,y=i-j+m;
int xx=(x-1)/d+1,yy=(y-1)/d+1;
if(xx&1)
{
if(yy&1) bel[i][j]=1;
else bel[i][j]=2;
}
else
{
if(yy&1) bel[i][j]=3;
else bel[i][j]=4;
}
}
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
{
if(bel[i][j]==1) printf("R");
if(bel[i][j]==2) printf("Y");
if(bel[i][j]==3) printf("G");
if(bel[i][j]==4) printf("B");
if(j==m) putchar('
');
}
return 0;
}