写在前面
图的存储结构有两种:一种是基于二维数组的邻接矩阵表示法。
另一种是基于链表的的邻接表表示法。
在邻接矩阵中,可以如下表示顶点和边连接关系:

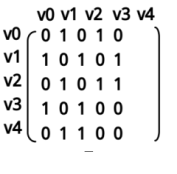
说明:
将顶点对应为下标,根据横纵坐标将矩阵中的某一位置值设为1,表示两个顶点向联接。
图示表示的是无向图的邻接矩阵,从中我们可以发现它们的分布关于斜对角线对称。
我们在下面将要讨论的是下图的两种遍历方法(基于矩阵的):
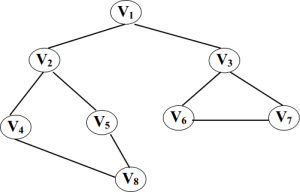
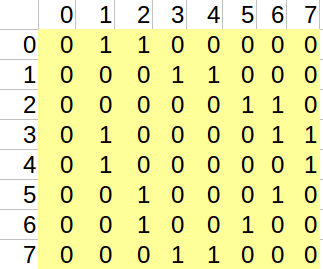
我们已经说明了我们要用到的是邻接矩阵表示法,那么我首先要来构造图:
1.深度优先遍历算法
分析深度优先遍历
从图的某个顶点出发,访问图中的所有顶点,且使每个顶点仅被访问一次。这一过程叫做图的遍历。
深度优先搜索的思想:
①访问顶点v;
②依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
③若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。
比如:
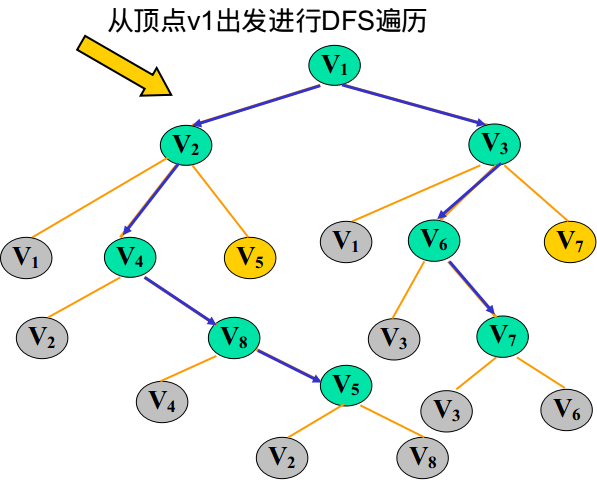
在这里为了区分已经访问过的节点和没有访问过的节点,我们引入一个一维数组bool visited[MaxVnum]用来表示与下标对应的顶点是否被访问过,
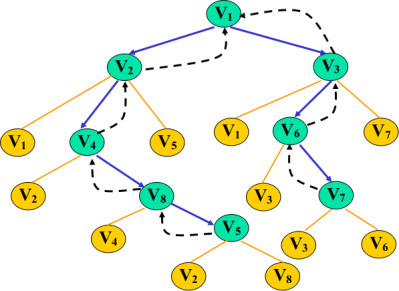
流程:
1)首先输出 V1,标记V1的flag=true;
2)获得V1的邻接边 [V2 V3],取出V2,标记V2的flag=true;
3)获得V2的邻接边[V1 V4 V5],过滤掉已经flag的,取出V4,标记V4的flag=true;
4)获得V4的邻接边[V2 V8],过滤掉已经flag的,取出V8,标记V8的flag=true;
5)获得V8的邻接边[V4 V5],过滤掉已经flag的,取出V5,标记V5的flag=true;
6)此时发现V5的所有邻接边都已经被flag了,所以需要回溯。(左边黑色虚线,回溯到V1,回溯就是下层递归结束往回返)
7)回溯到V1,在前面取出的是V2,现在取出V3,标记V3的flag=true;
8)获得V3的邻接边[V1 V6 V7],过滤掉已经flag的,取出V6,标记V6的flag=true;
9)获得V6的邻接边[V3 V7],过滤掉已经flag的,取出V7,标记V7的flag=true;
10)此时发现V7的所有邻接边都已经被flag了,所以需要回溯。(右边黑色虚线,回溯到V1,回溯就是下层递归结束往回返)
深度优先搜索的代码
2.广度优先搜索算法
分析广度优先遍历
所谓广度,就是一层一层的,向下遍历,层层堵截,还是这幅图,我们如果要是广度优先遍历的话,我们的结果是V1 V2 V3 V4 V5 V6 V7 V8。

广度优先搜索的思想:
① 访问顶点vi ;
② 访问vi 的所有未被访问的邻接点w1 ,w2 , …wk ;
③ 依次从这些邻接点(在步骤②中访问的顶点)出发,访问它们的所有未被访问的邻接点; 依此类推,直到图中所有访问过的顶点的邻接点都被访问;
说明:
为实现③,需要保存在步骤②中访问的顶点,而且访问这些顶点的邻接点的顺序为:先保存的顶点,其邻接点先被访问。 这里我们就想到了用标准模板库中的queue队列来实现这种先进现出的服务。
老规矩我们还是走一边流程:
说明:
1)将V1加入队列,取出V1,并标记为true(即已经访问),将其邻接点加进入队列,则 <—[V2 V3]
2)取出V2,并标记为true(即已经访问),将其未访问过的邻接点加进入队列,则 <—[V3 V4 V5]
3)取出V3,并标记为true(即已经访问),将其未访问过的邻接点加进入队列,则 <—[V4 V5 V6 V7]
4)取出V4,并标记为true(即已经访问),将其未访问过的邻接点加进入队列,则 <—[V5 V6 V7 V8]
5)取出V5,并标记为true(即已经访问),因为其邻接点已经加入队列,则 <—[V6 V7 V8]
6)取出V6,并标记为true(即已经访问),将其未访问过的邻接点加进入队列,则 <—[V7 V8]
7)取出V7,并标记为true(即已经访问),将其未访问过的邻接点加进入队列,则 <—[V8]
8)取出V8,并标记为true(即已经访问),将其未访问过的邻接点加进入队列,则 <—[]
两种表示法:
邻接矩阵完整代码:

#include<stdio.h> #include<stdlib.h> #include<malloc.h> //邻接矩阵 #define OK 1 #define ERROR 0 #define MAXNUM 10 typedef int Status; typedef char ElemType; typedef struct { int vnum; //顶点数 int anum; //弧/边数 ElemType vex[MAXNUM]; //存储顶点 int arc[MAXNUM][MAXNUM]; //存储边关系 }MGraph; int Location(MGraph G, ElemType e) { int v; for (v = 0; v<G.vnum; v++) if (G.vex[v] == e)return v; return -1; } Status CreateGraph(MGraph &G, int vnum, int anum, ElemType v[], ElemType a[]) //数组生成图 { int k; G.vnum = vnum; //获取数组顶点数 G.anum = anum; //获取数组边数 for (k = 0; k<G.vnum; k++) G.vex[k] = v[k]; for (int i = 0; i<G.vnum; i++) { for (int j = 0; j<G.vnum; j++) G.arc[i][j] = 0; } int t = 0; int p, q; for (k = 0; k<G.anum; k++) { ElemType m, n; m = a[t++]; n = a[t++]; t++; p = Location(G, m); q = Location(G, n); G.arc[p][q] = 1; G.arc[q][p] = 1; } return OK; } void Print(MGraph G) { int v; printf("顶点序列为: "); for (v = 0; v<G.vnum; v++) printf("%3c", G.vex[v]); printf(" "); printf("边的二维数组关系: "); for (int i = 0; i<G.vnum; i++) { for (int j = 0; j<G.vnum; j++) printf("%3d", G.arc[i][j]); printf(" "); } printf(" "); } int FirstAdjVex(MGraph G, int i) { int v; if (i<0 || i >= G.vnum)return -1; for (v = 0; v<G.vnum; v++) if (G.arc[i][v] == 1)return v; return -1; } int NextAdjVex(MGraph G, int i, int j) { if (i<0 || i >= G.vnum)return -1; if (j<0 || j >= G.vnum)return -1; for (int v = j + 1; v<G.vnum; v++) if (G.arc[i][v] == 1)return v; return -1; } //DFS遍历 int visited[MAXNUM]; void DFS(MGraph G, int v); void DFSTraverse(MGraph G) { printf("深度优先遍历为: "); int v; for (v = 0; v<G.vnum; v++) visited[v] = 0; for (v = 0; v<G.vnum; v++) { if (visited[v] == 0)DFS(G, v); } } void DFS(MGraph G, int v) { printf("%3c", G.vex[v]); visited[v] = 1; int w = FirstAdjVex(G, v); while (w != -1) { if (visited[w] == 0)DFS(G, w); w = NextAdjVex(G, v, w); } } //BFS遍历 typedef struct QNode { ElemType data; struct QNode *next; }QNode, *QueuePtr; //定义队列的指针类型为QueuePtr,定义队列结点内存空间类型为QNode typedef struct { QueuePtr front; //front为头指针,指向头结点。Q.front->next指针存在头结点的指针域(即其存着首结点的地址),是头结点的指针,指向首结点 QueuePtr rear; }LinkQueue; //定义队列结点类型为LinkQueue Status InitQueue(LinkQueue &Q) { Q.front = (QNode*)malloc(sizeof(QNode)); if (!Q.front)return ERROR; Q.front->next = NULL; Q.rear = Q.front; return OK; } Status EnQueue(LinkQueue &Q, ElemType e) //入队 { QueuePtr p; p = (QNode*)malloc(sizeof(QNode)); //生成新结点p if (!p)return ERROR; p->next = NULL; //新结点的指针p->next置空 p->data = e; //新结点暂存e Q.rear->next = p; //队尾结点的指针Q.rear->next指向新结点p Q.rear = p; //队尾指针Q.rear指向p return OK; } Status DeQueue(LinkQueue &Q, ElemType &e) //出队 { QueuePtr p; if (Q.rear == Q.front) //确保队列有首结点 return ERROR; p = Q.front->next; //指针p暂存被删结点(首结点)的地址 Q.front->next = p->next; //头结点的指针Q.front->next指向首结点的下一结点 e = p->data; if (Q.front->next == Q.rear) //判断原队列是否只有首结点 Q.rear = Q.front; free(p);//清空 return OK; } bool EmptyQueue(LinkQueue Q) //判空 { if (Q.front == Q.rear)return true; else return false; } void BFS(MGraph G) { printf("广度优先遍历为: "); int v; LinkQueue Q; InitQueue(Q); for (v = 0; v<G.vnum; v++) //初始化 visited[v] = 0; for (v = 0; v<G.vnum; v++) { if (visited[v] == 1)continue; printf("%3c", G.vex[v]); visited[v] = 1; EnQueue(Q, G.vex[v]); while (EmptyQueue == 0) { int v; ElemType e; DeQueue(Q, e); v = Location(G, e); int w = FirstAdjVex(G, v); while (w != -1) { w = NextAdjVex(G, v, w); if (visited[w] = 1)continue; printf("%3c", G.vex[w]); EnQueue(Q, G.vex[w]); visited[w] = 1; } } } } int main() { MGraph G; ElemType v[] = "abcdef"; //顶点数组 ElemType a[] = "ab,ac,ad,be,ce,df"; //边数组 CreateGraph(G, 6, 6, v, a); Print(G); DFSTraverse(G); printf(" "); BFS(G); printf(" "); system("pause"); return 0; }//
邻接表完整代码:

#include<stdio.h> #include<malloc.h> #define OK 1 #define ERROR 0 #define MAXNUM 10 typedef int Status; typedef char ElemType; typedef struct ANode { int adjvex; //邻接点域 struct ANode *next; //邻接点指针域 }ANode; //ANode为单链表的指针类型 typedef struct { ElemType data; ANode *firstarc; //定义单链表的头指针为firstarc }VNode; //VNode为顶点数组元素的类型 typedef struct { int vnum,anum; //顶点数,边数 VNode vex[MAXNUM]; //顶点集 }ALGraph; //ALGraph邻接表类型 int Location(ALGraph G, ElemType e) { int v; for (v = 0; v<G.vnum; v++) if (G.vex[v].data == e)return v; return -1; } Status CreatGraph(ALGraph &G, int vnum, int anum, ElemType v[], ElemType a[]) { int k, t = 0; G.vnum = vnum; G.anum = anum; for (k = 0; k<G.vnum; k++) { G.vex[k].data = v[k]; G.vex[k].firstarc = NULL;//易忘记 } for (k = 0; k<G.anum; k++) { ElemType m, n; ANode *p1, *p2, *p3; int p, q; m = a[t++]; n = a[t++]; t++; p = Location(G, m); q = Location(G, n); p1 = (ANode*)malloc(sizeof(ANode)); if (p1 == NULL)return ERROR; p1->adjvex = q; p1->next = NULL; if (G.vex[p].firstarc == NULL) G.vex[p].firstarc = p1; else { p3 = G.vex[p].firstarc; while (p3->next) p3 = p3->next; p3->next = p1; } p2 = (ANode*)malloc(sizeof(ANode)); if (!p2)return ERROR; p2->adjvex = p; p2->next = NULL; if (G.vex[q].firstarc == NULL) G.vex[q].firstarc = p2; else { p3 = G.vex[p].firstarc; while (p3->next) p3 = p3->next; p3->next = p2; } } return OK; } int FirstAdjVex(ALGraph G, int v) { if (v<0 || v >= G.vnum)return -1; if (G.vex[v].firstarc != NULL) return G.vex[v].firstarc->adjvex; return -1; } int NextAdjVex(ALGraph G, int v, int w) { ANode *p; p = G.vex[v].firstarc; if (v<0 || v >= G.vnum)return -1; if (w<0 || w >= G.vnum)return -1; while (p&&p->adjvex != w) p = p->next; if (p != NULL || p->next != NULL) return p->next->adjvex; return -1; } //DFS int visited[MAXNUM]; void DFS(ALGraph G, int v); void DFSTraverse(ALGraph G) { printf("深度遍历为: "); int v; for (v = 0; v<G.vnum; v++) visited[v] = 0; for (v = 0; v<G.vnum; v++) if (visited[v] == 0)DFS(G, v); printf(" "); } void DFS(ALGraph G, int v) { int w; printf("%3c", G.vex[v].data); visited[v] = 1; w = FirstAdjVex(G, v); while (w != -1) { if (visited[w] == 0)DFS(G, w); w = NextAdjVex(G, v, w); } } //BFS遍历-链队列 typedef struct QNode { ElemType data; struct QNode *next; }QNode, *QueuePtr; typedef struct { QueuePtr front; QueuePtr rear; }LinkQueue; Status InitQueue(LinkQueue &Q) { Q.front = (QNode*)malloc(sizeof(QNode)); if (!Q.front)return ERROR; Q.front->next = NULL; Q.rear = Q.front; return OK; } //入队 Status EnQueue(LinkQueue &Q, ElemType e) { QueuePtr p; p = (QNode*)malloc(sizeof(QNode)); if (!p)return ERROR; p->next = NULL; p->data = e; Q.rear->next = p; Q.rear = p; return OK; } //出队 Status DeQueue(LinkQueue &Q, ElemType &e) { QueuePtr p; if (Q.rear == Q.front) return ERROR; p = Q.front->next; Q.front->next = p->next; if (Q.front->next == Q.rear) Q.rear = Q.front; e = p->data; free(p);//清空 return OK; } //判空 bool EmptyQueue(LinkQueue Q) { if (Q.front == Q.rear)return true; else return false; } //BFS void BFS(ALGraph G) { printf("广度优先遍历为: "); int v; LinkQueue Q; InitQueue(Q); for (v = 0; v<G.vnum; v++)//初始化 visited[v] = 0; for (v = 0; v<G.vnum; v++) { if (visited[v] == 1)continue; printf("%3c", G.vex[v].data); visited[v] = 1; EnQueue(Q, G.vex[v].data); while (EmptyQueue == 0) { int v; ElemType e; DeQueue(Q, e); v = Location(G, e); int w = FirstAdjVex(G, v); while (w != -1) { w = NextAdjVex(G, v, w); if (visited[w] = 1)continue; printf("%3c", G.vex[w].data); EnQueue(Q, G.vex[w].data); visited[w] = 1; } } } } int main() { ALGraph G; ElemType v[] = "abcdef"; ElemType a[] = "ab,ac,ad,be,ce,df"; CreatGraph(G, 6, 6, v, a); DFSTraverse(G); BFS(G); getchar(); return 0; }