•题意
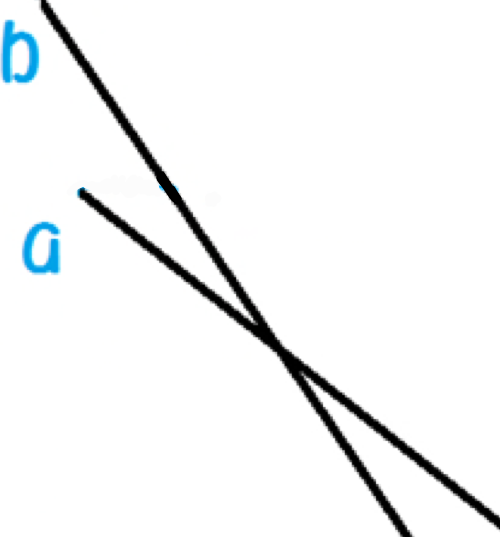
两根木块组成一个槽,给定两个木块的两个端点
雨水竖直下落，问槽里能装多少雨水,
•思路
找不能收集到雨水的情况
我们令线段较高的点为s点，较低的点为e点
①两条木块没有交点
②平行或重合
③至少有一条木块水平(雨水会滑落)
④形成覆盖，如"$wedge $"，"人"，还有比较难想的上边长下边短的情况
- 其中形成"$wedge$"型和"人"型 都是两条线段的交点比两条线段中较低的s点同高，
也就是不大于较高的s点
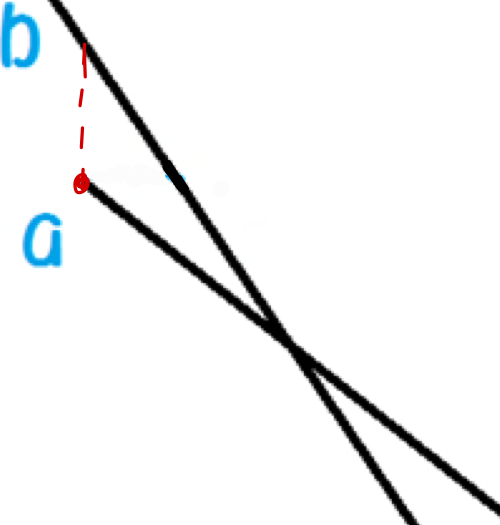
- 上长下短的覆盖是两个s点都大于交点而不能存水的唯一情况
如上图，我们可以在a.x出从b上引一条竖直线，看是否与a有交点，如果有说明覆盖了
能收集到雨水的情况要注意 水面与较低的s点水平
•代码
View Code1 //#include<bits/stdc++.h> 2 #include<iostream> 3 #include<cstdio> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 8 // `计算几何模板` 9 const double eps = 1e-12; 10 const double inf = 1e20; 11 const double pi = acos(-1.0); 12 const int maxp = 1010; 13 //`Compares a double to zero` 14 int sgn(double x){ 15 if(fabs(x) < eps)return 0; 16 if(x < 0)return -1; 17 else return 1; 18 } 19 //square of a double 20 inline double sqr(double x){return x*x;} 21 /* 22 * Point 23 * Point() - Empty constructor 24 * Point(double _x,double _y) - constructor 25 * input() - double input 26 * output() - %.2f output 27 * operator == - compares x and y 28 * operator < - compares first by x, then by y 29 * operator - - return new Point after subtracting curresponging x and y 30 * operator ^ - cross product of 2d Points 31 * operator * - dot product 32 * len() - gives length from origin 33 * len2() - gives square of length from origin 34 * distance(Point p) - gives distance from p 35 * operator + Point b - returns new Point after adding curresponging x and y 36 * operator * double k - returns new Point after multiplieing x and y by k 37 * operator / double k - returns new Point after divideing x and y by k 38 * rad(Point a,Point b)- returns the angle of Point a and Point b from this Point 39 * trunc(double r) - return Point that if truncated the distance from center to r 40 * rotleft() - returns 90 degree ccw rotated Point 41 * rotright() - returns 90 degree cw rotated Point 42 * rotate(Point p,double angle) - returns Point after rotateing the Point centering at p by angle radian ccw 43 */ 44 struct Point{ 45 double x,y; 46 Point(){} 47 Point(double _x,double _y){ 48 x = _x; 49 y = _y; 50 } 51 void input(){ 52 scanf("%lf%lf",&x,&y); 53 } 54 void output(){ 55 printf("%.2f %.2f ",x,y); 56 } 57 bool operator == (Point b)const{ 58 return sgn(x-b.x) == 0 && sgn(y-b.y) == 0; 59 } 60 bool operator < (Point b)const{ 61 return sgn(x-b.x)== 0?sgn(y-b.y)<0:x<b.x; 62 } 63 Point operator -(const Point &b)const{ 64 return Point(x-b.x,y-b.y); 65 } 66 //叉积 67 double operator ^(const Point &b)const{ 68 return x*b.y - y*b.x; 69 } 70 //点积 71 double operator *(const Point &b)const{ 72 return x*b.x + y*b.y; 73 } 74 //返回长度 75 double len(){ 76 return hypot(x,y);//库函数 77 } 78 //返回长度的平方 79 double len2(){ 80 return x*x + y*y; 81 } 82 //返回两点的距离 83 double distance(Point p){ 84 return hypot(x-p.x,y-p.y); 85 } 86 Point operator +(const Point &b)const{ 87 return Point(x+b.x,y+b.y); 88 } 89 Point operator *(const double &k)const{ 90 return Point(x*k,y*k); 91 } 92 Point operator /(const double &k)const{ 93 return Point(x/k,y/k); 94 } 95 //`计算pa 和 pb 的夹角` 96 //`就是求这个点看a,b 所成的夹角` 97 //`测试 LightOJ1203` 98 double rad(Point a,Point b){ 99 Point p = *this; 100 return fabs(atan2( fabs((a-p)^(b-p)),(a-p)*(b-p) )); 101 } 102 //`化为长度为r的向量` 103 Point trunc(double r){ 104 double l = len(); 105 if(!sgn(l))return *this; 106 r /= l; 107 return Point(x*r,y*r); 108 } 109 //`逆时针旋转90度` 110 Point rotleft(){ 111 return Point(-y,x); 112 } 113 //`顺时针旋转90度` 114 Point rotright(){ 115 return Point(y,-x); 116 } 117 //`绕着p点逆时针旋转angle` 118 Point Rotate(Point p,double angle){ 119 Point v = (*this) - p; 120 double c = cos(angle), s = sin(angle); 121 return Point(p.x + v.x*c - v.y*s,p.y + v.x*s + v.y*c); 122 } 123 }; 124 /* 125 * Stores two Points 126 * Line() - Empty constructor 127 * Line(Point _s,Point _e) - Line through _s and _e 128 * operator == - checks if two Points are same 129 * Line(Point p,double angle) - one end p , another end at angle degree 130 * Line(double a,double b,double c) - Line of equation ax + by + c = 0 131 * input() - inputs s and e 132 * adjust() - orders in such a way that s < e 133 * length() - distance of se 134 * angle() - return 0 <= angle < pi 135 * relation(Point p) - 3 if Point is on line 136 * 1 if Point on the left of line 137 * 2 if Point on the right of line 138 * Pointonseg(double p) - return true if Point on segment 139 * parallel(Line v) - return true if they are parallel 140 * segcrossseg(Line v) - returns 0 if does not intersect 141 * returns 1 if non-standard intersection 142 * returns 2 if intersects 143 * linecrossseg(Line v) - line and seg 144 * linecrossline(Line v) - 0 if parallel 145 * 1 if coincides 146 * 2 if intersects 147 * crossPoint(Line v) - returns intersection Point 148 * disPointtoline(Point p) - distance from Point p to the line 149 * disPointtoseg(Point p) - distance from p to the segment 150 * dissegtoseg(Line v) - distance of two segment 151 * lineprog(Point p) - returns projected Point p on se line 152 * symmetryPoint(Point p) - returns reflection Point of p over se 153 * 154 */ 155 struct Line{ 156 Point s,e; 157 Line(){} 158 Line(Point _s,Point _e){ 159 s = _s; 160 e = _e; 161 } 162 bool operator ==(Line v){ 163 return (s == v.s)&&(e == v.e); 164 } 165 //`根据一个点和倾斜角angle确定直线,0<=angle<pi` 166 Line(Point p,double angle){ 167 s = p; 168 if(sgn(angle-pi/2) == 0){ 169 e = (s + Point(0,1)); 170 } 171 else{ 172 e = (s + Point(1,tan(angle))); 173 } 174 } 175 //ax+by+c=0 176 Line(double a,double b,double c){ 177 if(sgn(a) == 0){ 178 s = Point(0,-c/b); 179 e = Point(1,-c/b); 180 } 181 else if(sgn(b) == 0){ 182 s = Point(-c/a,0); 183 e = Point(-c/a,1); 184 } 185 else{ 186 s = Point(0,-c/b); 187 e = Point(1,(-c-a)/b); 188 } 189 } 190 void input(){ 191 s.input(); 192 e.input(); 193 } 194 //根据x排序 195 void adjustx(){ 196 if(e < s)swap(s,e); 197 } 198 //根据y排序 199 void adjusty(){ 200 if(e.y>s.y) swap(s,e); 201 } 202 //求线段长度 203 double length(){ 204 return s.distance(e); 205 } 206 //`返回直线倾斜角 0<=angle<pi` 207 double angle(){ 208 double k = atan2(e.y-s.y,e.x-s.x); 209 if(sgn(k) < 0)k += pi; 210 if(sgn(k-pi) == 0)k -= pi; 211 return k; 212 } 213 //`点和直线关系` 214 //`1 在左侧` 215 //`2 在右侧` 216 //`3 在直线上` 217 int relation(Point p){ 218 int c = sgn((p-s)^(e-s)); 219 if(c < 0)return 1; 220 else if(c > 0)return 2; 221 else return 3; 222 } 223 // 点在线段上的判断 224 bool Pointonseg(Point p){ 225 return sgn((p-s)^(e-s)) == 0 && sgn((p-s)*(p-e)) <= 0; 226 } 227 //`两向量平行(对应直线平行或重合)` 228 bool parallel(Line v){ 229 return sgn((e-s)^(v.e-v.s)) == 0; 230 } 231 //`两线段相交判断` 232 //`2 规范相交` 233 //`1 非规范相交` 234 //`0 不相交` 235 int segcrossseg(Line v){ 236 int d1 = sgn((e-s)^(v.s-s)); 237 int d2 = sgn((e-s)^(v.e-s)); 238 int d3 = sgn((v.e-v.s)^(s-v.s)); 239 int d4 = sgn((v.e-v.s)^(e-v.s)); 240 if( (d1^d2)==-2 && (d3^d4)==-2 )return 2; 241 return (d1==0 && sgn((v.s-s)*(v.s-e))<=0) || 242 (d2==0 && sgn((v.e-s)*(v.e-e))<=0) || 243 (d3==0 && sgn((s-v.s)*(s-v.e))<=0) || 244 (d4==0 && sgn((e-v.s)*(e-v.e))<=0); 245 } 246 //`直线和线段相交判断` 247 //`-*this line -v seg` 248 //`2 规范相交` 249 //`1 非规范相交` 250 //`0 不相交` 251 int linecrossseg(Line v){ 252 int d1 = sgn((e-s)^(v.s-s)); 253 int d2 = sgn((e-s)^(v.e-s)); 254 if((d1^d2)==-2) return 2; 255 return (d1==0||d2==0); 256 } 257 //`两直线关系` 258 //`0 平行` 259 //`1 重合` 260 //`2 相交` 261 int linecrossline(Line v){ 262 if((*this).parallel(v)) 263 return v.relation(s)==3; 264 return 2; 265 } 266 //`求两直线的交点` 267 //`要保证两直线不平行或重合` 268 Point crossPoint(Line v){ 269 double a1 = (v.e-v.s)^(s-v.s); 270 double a2 = (v.e-v.s)^(e-v.s); 271 return Point((s.x*a2-e.x*a1)/(a2-a1),(s.y*a2-e.y*a1)/(a2-a1)); 272 } 273 //点到直线的距离 274 double disPointtoline(Point p){ 275 return fabs((p-s)^(e-s))/length(); 276 } 277 //点到线段的距离 278 double disPointtoseg(Point p){ 279 if(sgn((p-s)*(e-s))<0 || sgn((p-e)*(s-e))<0) 280 return min(p.distance(s),p.distance(e)); 281 return disPointtoline(p); 282 } 283 //`返回线段到线段的距离` 284 //`前提是两线段不相交，相交距离就是0了` 285 double dissegtoseg(Line v){ 286 return min(min(disPointtoseg(v.s),disPointtoseg(v.e)),min(v.disPointtoseg(s),v.disPointtoseg(e))); 287 } 288 //`返回点p在直线上的投影` 289 Point lineprog(Point p){ 290 return s + ( ((e-s)*((e-s)*(p-s)))/((e-s).len2()) ); 291 } 292 //`返回点p关于直线的对称点` 293 Point symmetryPoint(Point p){ 294 Point q = lineprog(p); 295 return Point(2*q.x-p.x,2*q.y-p.y); 296 } 297 //求线段交点 298 Point intersection(Line v) 299 { 300 double a1,a2,b1,b2,c1,c2; 301 a1=s.y-e.y; 302 a2=v.s.y-v.e.y; 303 b1=e.x-s.x; 304 b2=v.e.x-v.s.x; 305 c1=s.x*e.y-e.x*s.y; 306 c2=v.s.x*v.e.y-v.e.x*v.s.y; 307 return Point((c1*b2-c2*b1)/(a2*b1-a1*b2),(c1*a2-c2*a1)/(b2*a1-b1*a2)); 308 } 309 }; 310 int main() 311 { 312 int t; 313 scanf("%d",&t); 314 while(t--) 315 { 316 double a,b,c,d; 317 Line l1,l2,l3,l4; 318 scanf("%lf%lf%lf%lf",&a,&b,&c,&d); 319 l1=Line(Point(a,b),Point(c,d)); 320 scanf("%lf%lf%lf%lf",&a,&b,&c,&d); 321 l2=Line(Point(a,b),Point(c,d)); 322 l1.adjusty(),l2.adjusty(); 323 324 double s=-1; 325 if(l1.parallel(l2))///平行或重合 326 s=0; 327 else if((!l1.angle())||(!l2.angle()))///k=0 328 s=0; 329 else if(l1.segcrossseg(l2)==0)///不相交 330 s=0; 331 else if(l1.segcrossseg(l2))///相交 332 { 333 Point P=l1.intersection(l2);///获得交点 334 Point p1,p2; 335 int flag=0,flag1=0; 336 if(l1.s.y-P.y>eps) p1=l1.s,flag=1; 337 if(l2.s.y-P.y>eps) p2=l2.s,flag1=1; 338 if(flag&&flag1) 339 {///还有一种情况没有水。上面的y把下面的y覆盖---遮挡判断 340 if(p1.y-p2.y>eps) 341 { 342 if(l1.segcrossseg(Line(p2,Point(p2.x,p1.y+2.0)))) 343 { 344 printf("0.00 "); 345 continue; 346 } 347 } 348 if(p2.y-p1.y>eps) 349 { 350 if(l2.segcrossseg(Line(p1,Point(p1.x,p2.y+2.0)))) 351 { 352 printf("0.00 "); 353 continue; 354 } 355 } 356 if(p1.y-p2.y>eps) 357 { 358 ///取p1.x的水平和p2.y,p1与p2.x的交点 359 ///水面和低处水平 360 double x=p1.x>0?p1.x+1.00:p1.x-1.0; 361 p1=l1.intersection(Line(Point(x,p2.y),Point(-x,p2.y))); 362 } 363 else 364 { 365 double x=p2.x>0?p2.x+1.00:p2.x-1.0; 366 p2=l2.intersection(Line(Point(x,p1.y),Point(-x,p1.y))); 367 } 368 s=fabs((p1.x-p2.x)*(p1.y-P.y)*0.5)+eps; 369 } 370 else 371 s=0; 372 } 373 printf("%.2f ",s); 374 } 375 }
