FAST LOW-RANK APPROXIMATION FOR COVARIANCE MATRICES

目录

• Nystorm method
• 低秩逼近
  • 矩阵乘法的逼近

Belabbas M A, Wolfe P J. Fast Low-Rank Approximation for Covariance Matrices[C]. IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, 2007: 293-296.

Nystorm method

和在WIKI看到的不是同一个东西？

假设(G in mathbb{R}^{n imes n})为对称正定矩阵。

[G = left [ egin{array}{ll} A & B^T \ B & C end{array} ight ] ]

其中(A in mathbb{R}^{k imes k}, k<n)。
假设(G = U Lambda U^T),(A = U_A Lambda_A U_A^T),令

[widetilde{U} = left [ egin{array}{c} U_A \ BU_A Lambda_A^{-1} end{array} ight ] ]

则：

[widetilde{G} := widetilde{U} Lambda_A widetilde{U}^T = left [ egin{array}{ll} A & B^T \ B & BA^{-1}B^T end{array} ight ] ]

易得：

[|G - widetilde{G}| = |C-BA^{-1}B^T| ]

再玩一下，令：

[G = left [ egin{array}{lll} A_1 & A_2^T & A_3^T \ A_2 & M & B^T \ A_3 & B & C end{array} ight ] ]

且(M = U_M Lambda_M U_M^T).
再令

[widetilde{U} := left [ egin{array}{c} A_2^TU_M Lambda_M^{-1} \ U_M \ B U_M Lambda_M^{-1} end{array} ight ] ]

则：

[widetilde{G} := widetilde{U} Lambda_M widetilde{U}^T = left [ egin{array}{ccc} A_2^T M^{-1} A_2 & A_2^T & A_2^T M^{-1} B^T \ A_2 & M & B^T \ BM^{-1}A_2 & B & BM^{-1} B^T end{array} ight ] ]

这个阵型还蛮酷的。

低秩逼近

先来介绍一个性质：(F(F^TF)^{-1/2})列正交（当然(F^TF)得可逆）。

[(F(F^TF)^{-1/2})^TF(F^TF)^{-1/2} = (F^TF)^{-1/2}F^TF(F^TF)^{-1/2} = I ]

实际上，如果(F^TF = VLambda V^T)，那么(FV_k Lambda_k^{-1/2})列正交。
所以，我们可以让(F)的列为(G)中某些列的组合，再让(P_k := FV_k Lambda_k^{-1/2}),最后：

[widetilde{G}_k := P_kP_k^TGP_kP_k^T ]

来作为(G)的一个近似。

矩阵乘法的逼近

如果我们能够令(|GG^T-FF^T|)尽可能小，那么(P_kP_k^TG)就越有可能成为一个好的逼近，这需要利用矩阵乘法的逼近。
对于矩阵(A in mathbb{R}^{m imes n})和(B in mathbb{R}^{n imes p})，得：

[AB = sum_{i=1}^n A_iB^i ]

其中(A_i)为(A)的第i列，(B^i)为(B)的第i行。
论文举了一个例子：
如果(n=2)，且(A_2 = sqrt{alpha} A_1),(B=A^T)，
那么(AB = (1+alpha)A_1A_1^T)。这意味着，我们只需通过(A)的第一列就能恢复(AB)。
所以接下来的问题是：

• 如何选择行或者列
• 如何调整它们的大小（乘个系数）

作者说，有一个神谕说列和行应该为(S subset {1, ldots, n})，不失一般性，假设其为(S = {1, ldots, k})。下面的定理给出了权重的选择：

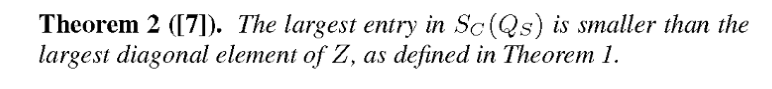
所以我们要挑选(S),使得(Z)的对角线元素尽可能小，这意味着，我们要挑选这样的(S),使得(<A_i, A_i><B^i, B^i>)最大。
于是有了下面的俩个算法，分别针对矩阵乘法和矩阵逼近的：