θ不一定完全可求出
那么需要让机器一步一步的去试验
比如下图，目前在一个中间点
梯度下降：得到一个目标函数后，如何进行求解？（不一定能够直接求解出来，线性回归只是一个特例）
对θ求偏导得到最陡的一个方向
得到的偏导数，就是一个梯度
正常的梯度是向上的，现在需要向下方向
也就是梯度上升的反方向
每次走一小点，一步一步往下走，走到最低点（第N步）就相当于这个事干完了
相当于得到近似的最优解。
常规套路：交给机器一堆数据，然后告诉它什么样的学习方式是对的（目标函数），然后让它朝着这个方向去做
如何优化：一步一步的完成整个迭代，每次优化一点点（通常优化1-10万次）
如果参数多的话，那么就需要每次求一个参数的偏导进行更新，比如下图
目标函数：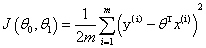
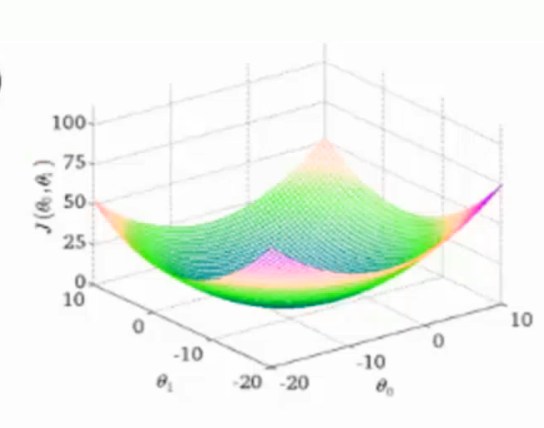
寻找山谷的最低点，也就是目标函数的终点，也就是什么样的参数能够使目标函数达到极值点
分几步方法：
1，找到合适的方向。随机点都行。走一小步。
2，只能走一小步，走快了有时候丢失精度，会直接跨过最小值点。
3，按照方法与步伐大小来更新参数
梯度下降的目标函数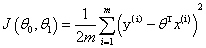：，另一个名称叫做损失函数，损失越小不就是越好么？
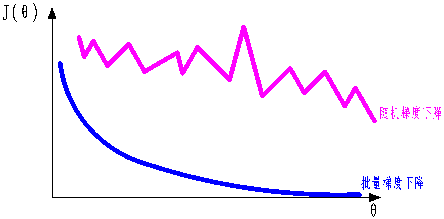
1，批量梯度下降：（带入所有的样本，可以得到最优解，计算量非常大，速度慢）
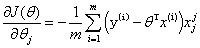
2，随机梯度下降：（每次找到一个样本，迭代速度快，但不一定每次都朝着收敛方向）
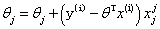
3，小批量梯度法：（每次选择一小部分数据样本来计算，相当于取前两个方法的中间方法，比较实用）
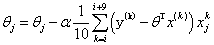
学习率（步长）：会对结果产生巨大的影响，一般选择小一点，步长也就是每次θ的差值，第一次与第二次θ的差值
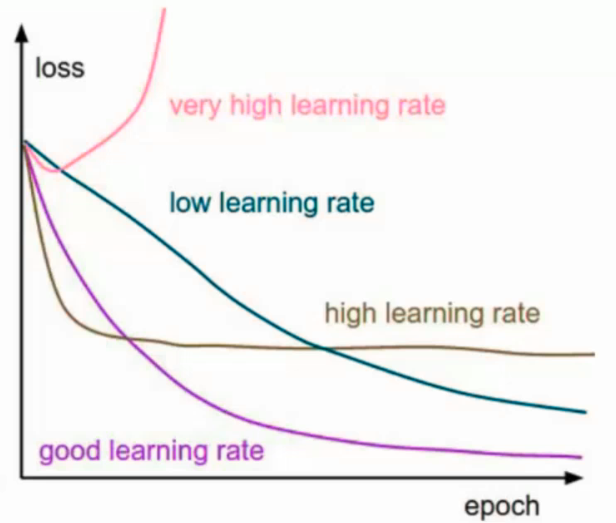
选大了速度快，精度低，选小了速度慢，精度高，用时间换空间
如何选择：从小的时候选择，不行的话在小，0.1不行0.01
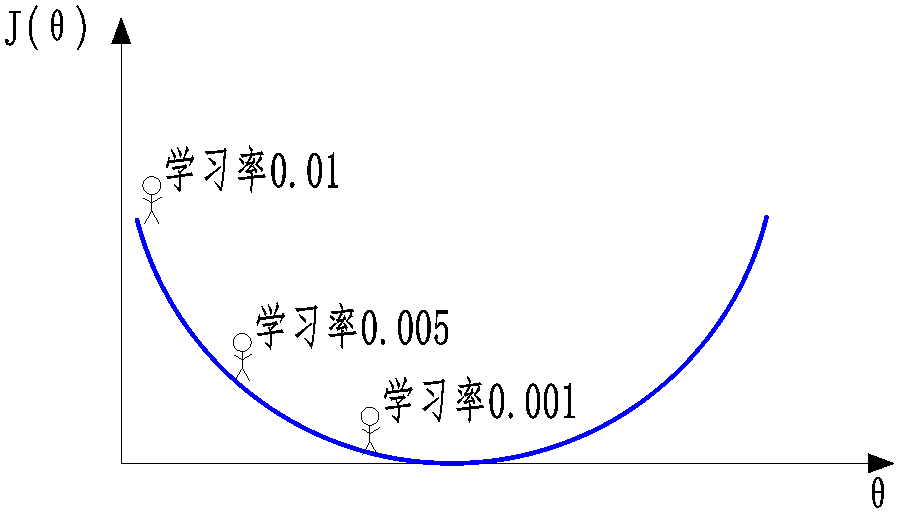
学习率其实是可以变动的，刚开始的时候选择大一些，越接近底部就可以选择越小
比如前多少条数据0.01，然后多少条数据0.005，然后0.001
批量处理量：32,64,128都可以一般是2的幂（容忍程度内，越大越好），很多时候考虑内存效率。
唐宇迪机器学习视频笔记——梯度下降算法