【计蒜客习题】灌溉机器人

问题描述

农田灌溉是一项十分费体力的农活，特别是大型的农田。蒜头君想为农民伯伯们减轻农作负担，最近在研究一款高科技——灌溉机器人。它可以在远程电脑控制下，给农田里的作物进行灌溉。
现在有一片 N 行 M 列的农田。农田的土壤有两种类型：类型 HH 和类型 PP，每一个格子上的土壤类型相同。其中类型 P 的土壤硬度较大，可以用来布置灌溉机器人，但是一个格子上只能布置一台。类型 H 的土壤不能布置灌溉机器人。一台灌溉机器人的灌溉区域如下图所示：

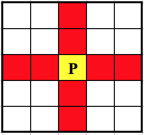
黄色表示灌溉机器人布置的格子，红色表示其灌溉区域，即四个方向上各外扩展两个格子。
蒜头君想在农田上尽可能多布置一些灌溉机器人，但是任意一台机器人不能在任意一台机器人的灌溉区域里，否则机器容易进水出故障。现在已知农田每个格子的土壤类型，请你来帮蒜头君计算一下，蒜头君最多能布置多少台灌溉机器人。

输入格式

输入第一行输入两个正整数N,M(N≤100,M≤10)，表示农田的行和列。
接下来输入 N 行，每行输入连续的 M 个字符（P或者H），中间没有空格。表示农田每个格子上的土壤类型。

输出格式

输出一行，输出一个整数，表示最多能摆放的灌溉机器人的数量

样例输入

3 4
PHPP
PHPP
PHHP

样例输出

3

---

呃呃，一道状压DP入门题。

没什么好说的，注意先预处理一下，发现若要满足同一行不冲突，情况最多有60种。定义dp[i][j][k]表示处理到第i行，当前行选择方案为j，上一行选择方案为k时最多的摆放数量，这样就可以保证只需知道当前行的dp和上一行的dp就可以知道对当前行选择方案有影响的上一行和上上一行，转移方程显然是dp[i][j][k]=max{dp[i-1][k][l]+count(j)}，count返回某一方案的机器人数量。再就是冲突时的判断需要写好。

#include<cstdio>
inline int max(int a,int b) {return a>b?a:b;}
const int maxn=105,maxm=15;
//经预先验证，满足同一行不冲突的情况最多有60种
int n,m,map[maxn],state[65],cnt,dp[maxn][65][65],ans;
bool judge1(int x) {
    return (x&(x>>1))==0&&(x&(x>>2))==0;
}
bool judge2(int i,int j) {
    return (j|map[i])==map[i];
}
bool judge3(int x,int y) {
    return (x&y)==0;
}
int count(int i) {
    int c=0;
    while(i) {
        if(i&1) ++c;
        i>>=1;
    }
    return c;
}
int main() {
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;++i) {
        int si=0;char c;
        for(int j=0;j<m;++j) {
            while((c=getchar())=='
'||c==' '||c=='
');
            if(c=='P') si|=(1<<j);
        }
        map[i]=si;
    }
    for(int i=0;i<(1<<m);++i) if(judge1(i)) state[++cnt]=i;
    for(int i=1;i<=cnt;++i) if(judge2(1,state[i])) {
        int cnt_i=count(state[i]);
        for(int j=1;j<=cnt;++j) dp[1][i][j]=cnt_i;
    }
    for(int i=2;i<=n;++i)
        for(int j=1;j<=cnt;++j) if(judge2(i,state[j])) {
            int cnt_j=count(state[j]);
            for(int k=1;k<=cnt;++k) if(judge2(i-1,state[k])&&judge3(state[j],state[k]))
                for(int l=1;l<=cnt;++l)
                    if(judge2(i-2,state[l])&&judge3(state[k],state[l])&&judge3(state[j],state[l]))
                        dp[i][j][k]=max(dp[i][j][k],dp[i-1][k][l]+cnt_j);
        }
    for(int i=1;i<=cnt;++i)
        for(int j=1;j<=cnt;++j) ans=max(ans,dp[n][i][j]);
    printf("%d",ans);
    return 0;
}