回忆一下高中时学的万有引力定律那一部分的知识:离恒星越远的行星,线速度越慢。
具体一点来说,因为向心力由万有引力提供,所以:
可以推出:
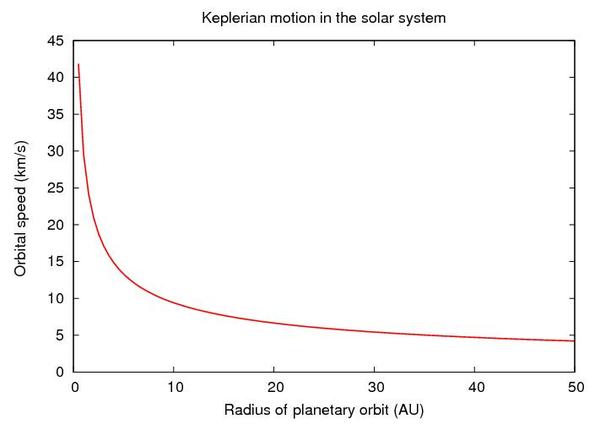
同样地,对于一个旋转的星系来说,其线速度与轨道半径关系大致应该是这样(图片均来自网络):
然而当我们实际观测星系的时候,(利用光谱红移等等现象)发现线速度与半径的关系完全不是这样!!而是这样(图中B曲线):

随着轨道半径的增加,线速度竟然趋近一个常数!
这里有视频:https://link.zhihu.com/?target=https%3A//en.wikipedia.org/wiki/File%3AGalaxy_rotation_under_the_influence_of_dark_matter.ogv
这怎么解释?
于是人们推测,可能星系中存在大量我们目前观测不到的物质,使得星系密度与半径有如下关系:
,K是一个常数。
根据 Newton's Shell Theorem 可得:
(依然是向心力等于万有引力,但万有引力只跟距离r以内的质量有关系。)
两边消去m,
那么距离r以内的质量怎么计算呢?
上式其实就是质量等于体积乘密度啦,只不过因为密度随距离变化,所以需要用积分。带入之前的式子里,得到:
化简得到:
当我们假设了存在观测不到的物质后,就是一个常数了!!
而且当我们知道线速度之后,就可以算出的值。
代入到密度的函数中:
于是星系的质量为:
一般来说,星系的半径在100~200kpc之间(这里我代入100kpc),线速度约为220km/s。于是可以算出星系的质量约为:
而太阳的质量约为:
也就是说,
而我们能观测到的星系质量约为:
所以,这么算下来我们能观测到的质量大概只占总质量的10%,如果代入更大的,就发现这个比例更小。
评论里有人问可观测的质量是怎么知道的。
方法有不少,我大概说一下:可以通过观测binary stars(联星)的运动算出来;也可以通过luminosity(光度)与质量之间的关系算出来;也可以通过恒星oscillate的轨迹算出其密度,然后求得质量。
知道了各种恒星的质量之后,就可以测量它们发出的光,然后计算它们各自的M/L(Mass-to-light ratio)。然后对于一个给定的星系,观测其发出的光,然后乘上M/L,就可以得到星系的质量了。
来自知乎:https://www.zhihu.com/question/35511154#answer-24163708
知乎上真是各路大神。