下面三张图的模型分别是:y=θ0+θ1x,y=θ0+θ1x+θ2x2,y=θ0+θ1x+…θ5x5。
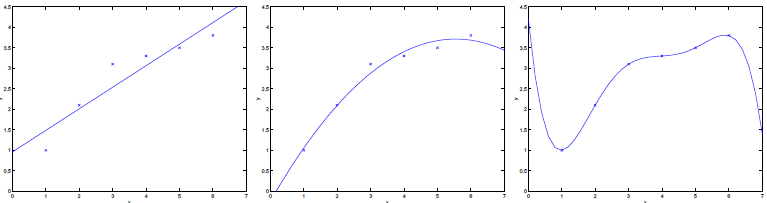
第一幅图和第三幅图都有很大的泛化误差,但它们的问题是不一样的。第一幅图的问题是欠拟合,y 和 x 的关系不是线性的,但我们非要用线性模型去拟合,即使有大量的训练数据,也不能精确捕捉到数据中隐藏的结构信息,这种情况被称为模型的偏差。第三幅图的问题是过拟合,使用五阶多项式来拟合数据,就有很大的风险是,我们拟合得到的模型,仅仅适用于当前的小量的、有限的训练数据集,不能代表 y 和 x 在更大范围的关系模式,譬如在训练集中的房屋价格在这里只是随机地比均值低,在另一处又随机地比均值高,如果训练集中的这种假的模式都要捕捉,那必定要产生巨大的泛化误差,这种情况被称为模型的方差。
偏差和方差之间常常有一个权衡。如果模型很简单,参数很少,那么偏差就会很大,但方差小。如果模型很复杂,参数很多,那就可能有很大的方差,但偏差很小。上例中,二次函数明显比一阶和五阶多项式好。
下面开始介绍学习理论,这有助于磨练我们的直觉,给出在不同情况下更好地应用学习算法的准则。我们将试图回答这些问题:首先,我们能不能形式化偏差/方差的权衡?这最终会引导我们讨论模型选择方法,例如自动决定使用何阶多项式来拟合训练集;其次,在机器学习中最关心泛化误差,大多数学习算法都在训练数据中拟合模型,为什么训练集中表现好会告诉我们关于泛化误差的情况?训练集的误差和泛化误差有关联吗?最后,有没有什么条件,可以证明一种学习算法好?
先来两个简单有用的定理:
定理1:设 A1,A2,...Ak 为 k 个不同的事件(它们不一定独立),那么 P(A1∪...∪Ak)≤P(A1)+...P(Ak)
定理2:设 Z1,...,Zm 为 m 个独立同分布的随机变量,都服从伯努利分布 Bernoulli(Φ) ,P(Zi=1)=Φ,P(Zi=0)=1-Φ。设 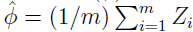 为随机变量的均值,设 γ>0 为定值,得:
为随机变量的均值,设 γ>0 为定值,得:
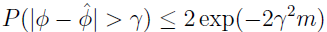
也称 Hoeffding 不等式。
我们先来考察下不等式的右边,先看当 γ 为定值(分别为 0.2、0.3、0.4)时,右边值的变化情况,再看 m 为定值(分别是 20、50、80)时,右边值的变化。如下图所示。加号展开即是绘图 Python 代码。

import numpy as np import matplotlib.pyplot as plt fig = plt.figure() #当 gama 为定值时,不等式右边值随 m 的变化 m=np.linspace(1,100,100) gama=0.2 p=2*np.exp(-2*m*(gama**2)) ax=fig.add_subplot(231) ax.set_title('gama=0.2') ax.set_xlabel('m') ax.set_ylabel("2exp(-2mgama^2)") plt.sca(ax) plt.plot(m,p) gama=0.3 p=2*np.exp(-2*m*(gama**2)) ax=fig.add_subplot(232) ax.set_title('gama=0.3') ax.set_xlabel('m') plt.sca(ax) plt.plot(m,p) gama=0.4 p=2*np.exp(-2*m*(gama**2)) ax=fig.add_subplot(233) ax.set_title('gama=0.4') ax.set_xlabel('m') plt.sca(ax) plt.plot(m,p) #当 m 为定值时,不等式右边值随 gama 的变化 gama=np.linspace(0.01,1,100) m=20 p=2*np.exp(-2*m*(gama**2)) ax=fig.add_subplot(234) ax.set_title('m=20') ax.set_xlabel('gama') ax.set_ylabel("2exp(-2mgama^2)") plt.sca(ax) plt.plot(gama,p) m=50 p=2*np.exp(-2*m*(gama**2)) ax=fig.add_subplot(235) ax.set_title('m=50') ax.set_xlabel('gama') plt.sca(ax) plt.plot(gama,p) m=80 p=2*np.exp(-2*m*(gama**2)) ax=fig.add_subplot(236) ax.set_title('m=80') ax.set_xlabel('gama') plt.sca(ax) plt.plot(gama,p) plt.show()

从上图可以看出,当 γ 和 m 增大时,不等式右边值随着减小。也就是说,当 m 增大时,Φ 尖和 Φ 的误差是变小的。
这个定理是说,当 m 很大时,如果我们通过 Φ 尖来估计 Φ,那么它偏离真实值的概率是很小的。还有种说法,如果你抛一枚不均衡的硬币 m 次,那么以头向上的比例来估计头朝上的概率 Φ,那么它就有很大的概率是个好估计。
用这两个定理,就可以证明学习理论中一些深刻的、重要的结论。
为叙述简单起见,下面只关注二分类,y∈{0,1},此处讲的所有内容都可以推广到其它问题,如回归和多分类问题。
设有训练集 S={(x(i),y(i));i=1,...,m} ,训练集 (x(i),y(i)) 由同一概率分布 D 生成,对于假设 h,定义训练错误为:
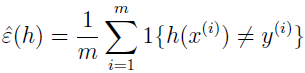
在学习理论中也称为经验风险或者经验错误。
这是 h 在训练集上误分类的比例。要明确 ε(h) 尖对训练集 S 的依赖关系时,也可以写成 εS(h)。我们也定义泛化误差为
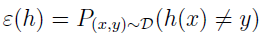
这个概率表示,如果从分布 D 中生成一个新例子 (x,y) ,h 会给它分错类。
注意我们假定训练数据来自同一分布 D,我们将通过泛华误差的定义来评估假设。有时这也是 PAC 的假设之一。
考虑线性分类的情况,使 hθ(x)=1{θTx≥0},拟合参数 θ 的合理方法是什么?我们的方法是最小化训练误差:
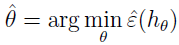
这个过程称为经验风险最小化(ERM),输出的结果假设是学习算法![]() ,ERM 是最基础的学习算法,像 Logistic 回归也被看作经验风险最小化的估计。
,ERM 是最基础的学习算法,像 Logistic 回归也被看作经验风险最小化的估计。
在学习理论的研究中,从特定的参数化假设或题目如是否使用线性分类器中抽离出来是很有用的,我们定义学习算法使用的假设类 H 为所有分类器的集合,对于线性分类,H={hθ : hθ(x)=1{θTx≥0},θ∈Rn+1} 是所有线性决策边界的分类器的集合。再比如,如果学习神经网络,就可以使 H 为代表一些神经网络架构的分离器集合。
经验风险最小化可以被认为是函数类 H 中的最小化,学习算法选择假设:
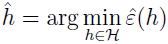
先来看个学习问题,有限假设类 H={h1,...,hk} 由 k 个假设组成。所以 H 是 k 个从 X 到 {0,1} 的映射函数的集合,经验风险最小化选择 h^ 为这 k 个函数有最小的训练误差。
我们要对 h 尖的泛华误差进行担保。分两步进行:第一步,证明对于对于所有的 h,ε^(h) 都是 ε(h) 的可靠估计,第二步,证明 h^ 的泛化误差是有上界的。
取任意一个固定的 hi∈H,有一个伯努利随机变量 Z,分布定义如下,采样 (x,y)~D,设 Z=1{h(x)≠y},即,取个例子,让 Z 表示 hi 有没有错分。类似的,定义 Zj=1{hi(x(j))≠y(j)},训练集来自独立同分布 D,Z 和 Zj 来自同一分布。
可以看出,在随机例子中的误分概率 ε(h) 正好是 Z(Zj) 的期望值。而且,训练误差可写为
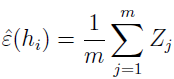
所以 ε^(hi) 正好是 m 个随机变量 Zj 的均值,Zj 是来自均值为 ε(h) 的伯努利分布。所以,我们可以使用 Hoeffding 不等式
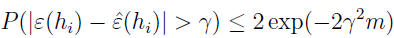
这表示,对于特定的 hi,假定 m 很大,训练误差以很高的概率接近泛化误差,但我们不仅仅只是想担保特定的 ε^(hi) 以高概率趋近 ε(hi),而是要证明所有的 h 都这样。为此,设 A 表示事件 |ε(hi)-ε^(hi)|>γ,已经证明,对于特定的 Ai,有 P(Ai)≤2exp(-2γ2m),所以有

两边都由 1 减去,得

也就是说,至少有 1-2kexp(-2γ2m) 的概率,对于所有的 h,ε(h) 和 ε^(h) 之间相差 γ,称为均匀收敛结果。
在上面的讨论中,对于特定的 m 和 γ,对概率给定一个界限,对于 h∈H,|ε(h)-ε^(h)|>γ ,这里有三个量化点:m,γ 和错误概率。我们可以变动任意一个,依据另外两个。
例如问题,给定 γ 和 δ>0,那么 m 为多大才能保证训练误差和泛化误差之差 γ 的概率为 1-δ?设 δ=2kexp(-2γ2m),解出 m。我们发现当
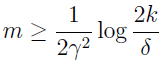
时,至少 1-δ 的概率,对于所有的 h∈H,有 |ε(h)-ε^(h)|≤γ(因为至多有 δ 的概率使 |ε(h)-ε^(h)|>γ),这个界可以告诉我们需要多少例子来做保证。为使算法达到一定性能所需的训练集大小 m 被称为采样复杂度。
上面界限的一个关键属性是 k 的 log 值,H 中的假设个数,这在后面很重要。
类似的,也可以固定 m 和 δ,解出 γ,那么就有 1-δ 的概率有
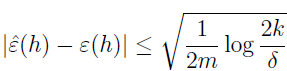
现在假设满足均匀收敛条件,即对所有的 h∈H,有 |ε(h)-ε^(h)|≤γ。那么取 h^=argminh€Hε^(h),关于学习算法的泛化,能证明什么?
定义 h*=argminh€Hε(h) 为 H 中最好的假设。有
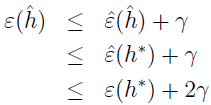
第一行根据 |ε(h^)-ε^(h^)|≤γ,即通过均匀收敛假设。
第二行根据 h^=argminh€Hε^(h),所以 ε^(h^)≤ε^(h),特别的,ε^(h^)≤ε^(h*)。
第三行再次根据均匀分布假设,ε^(h*)≤ε(h*)+γ。
上式表示,如果均匀收敛,那么 h^ 的泛化误差至多比 H 中最好的假设 h* 坏 2γ。
我们把这些合成一个定理。
定理:设 |H|=k,设 m,δ 为定值,那么至少有 1-δ 的概率
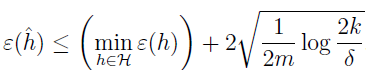
证明此式,只需使 γ 等于根号部分,然后使用上面的结果即可。
这就量化了我们之前讲的模型选择中,偏差和方差的权衡。假设有一些假设类 H,现在切换到一个更大的假设类 H‘⊇H,那么第一项 minhε(h) 只可能减少,因为我们从一个更大的函数集合中取最小。所以,学习使用一个更大的假设类,我们的偏差只会减少。如果 k 增加,那么第二项 2√· 也会增加,即方差也会增加。(参考文 3 的解释:当选择一个复杂的模型假设时,|H|=k 会变大,导致不等式后的第二项变大,意味着方差变大,但第一项又会变小,因为使用一个更加大的模型集合,意味着可供选择的模型假设变多了,在多的那部分中可能有比原来还要小的模型,这样偏差就会变小。选择一个最优值,使得偏差与方差之和最小,才能得到一个好的模型)
令 γ 和 δ 固定,跟之前一样解出 m,就得到下面的采样复杂度界限。
推论:令 |H|=k,固定 δ 和 γ,那么至少有 1-δ 的概率使 ε(h^)≤minh€Hε(h)+2γ。它满足
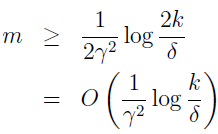
现在,我们证明了有限假设类的一些有用的理论。但有许多假设类包含了无数的函数,如参数为实值的,如线性分类中。这种情况也能得到类似证明吗?
先来看一些不是正确的讨论,更好和更多的广义参数是存在的,这对于磨练我们在这个领域的直接是很有用的。
假设 H 有 d 个实值参数,因为我们用电脑来表示实数值,IEEE 的双精度浮点用 64 位比特来表示一个浮点数,假定使用双精度浮点数,这意味着我们的学习算法参数有 64d 位,所以,我们的假设类是由至多 k=264d 个不同的假设组成。从上面的推论可得,为保证至少有 1-δ 的概率,使 ε(h^)≤ε(h*)+2γ,它满足
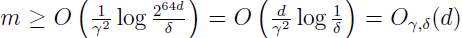
下标 γ 和 δ 表示大 O 隐藏了依赖于 γ 和 δ 的常数。
所以,所需的训练集数目至多跟模型参数呈线性关系。
64 位浮点数表示参数的事实并不完全对,但结论无疑是正确的。如果想最小化训练误差,为了用好 d 个参数的假设类,通常使用跟 d 呈线性关系的训练例子数目。
在这一点上,值得一提的是,这些结果是只被使用经验风险最小化(ERM)的算法所证明,所以,对于大多数试图最小化训练误差的判别学习算法,对 d 的采样复杂度的线性依赖满足时,这些结论并不总能应用到判别学习算法。对很多非 ERM 学习算法一个理论保证,依然是一个研究热点。
之前的讨论的另一部分,对于 H 的参数的依赖就不太让人满意了。直观上,好像没多大关系:线性分类器为 hθ(x)=1{θ0+θ1x1+...+θnxn≥0},有 n+1 个参数 θ0,...,θn,但它也可以写成 h(x)=1{(u02-v02)+(u12-v12)x1+...+(un2-vn2)xn≥0},有 2n+2 个参数 ui,vi。这些都定义了同一个 H:n 维线性分类器的集合。
为了导出一个更加满意的结果,我们再来定义一些东西。
给定一个集合 S={x(i),...,x(d)}(跟训练集没关系),点 x(i)∈X,如果 H 能识别 S 的一些标签,那么就说 H 分散了 S。例如,如果对于一些标签集合 {y(1),...,y(d)},那么对于所有的 i=1,..,d,存在 h∈H 使 h(x(i))=y(i)。
给定假设类 H,我们能定义它的 Vapnik-Chervonenkis dimension,记作 VC(H),为被 H 分散的最大集合的大小。(如果 H 能分散任意大的集合,那么 VC(H)=∞)。
例如,考虑下面三个点的集合:
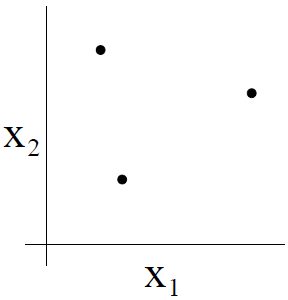
两维的线性分类器(h(x)=1{θ0+θ1x1+θ2x2≥0})的集合 H 能分散这个点集吗?可以。对于 8 个可能的标签组合,我们能找到一个线性分类器来获得一个 0 训练误差:
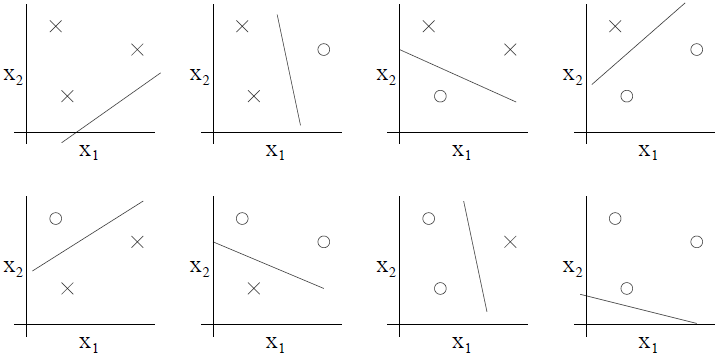
进一步,可能有 4 个点的集合不能被假设类分散,所以,H 能分散的最大集是 3,所以,VC(H)=3。
注意,这里即使有 3 个点的集合不能被分散,H 的 VC 维依然是 3。例如如果有三个点在一条直线上,就不能用线性分类器分开。但这无关紧要,只要存在一个三个点的集合,不论以任何的标记方式,直线集合都能将其线性分开的话,就认为直线集合能分散的点的数目是 3。对于 4 个点的集合,不存在一个 4 点集合,无论以任何标记方式,都能将其用线性分类器分开,所以,就得到,在二维平面上,对于直线集合,它能分散的点的最大数目是 3。
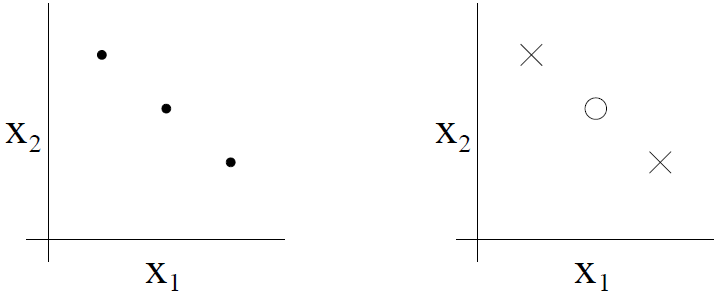
换句话说,在 VC 维的定义下,为了证明 VC(H) 至少是 d,我们要展示的仅仅是存在至少有一个大小为 d 的集合 H 能分散。
下面的定理,根据 Vapnik,能被证明。这是学习理论中最重要的定理。
定理:给定 H,使 d=VC(H),那么至少有 1-δ 的概率,对于所有 h∈H,有
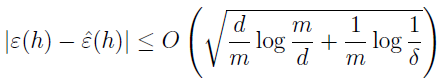
所以,至少有 1-δ 的概率,有
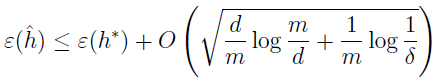
换句话说,如果一个假设类有有限 VC 维,那么当 m 变得很大时,就会均匀收敛。跟之前一样,这允许我们可以给 ε(h) 一个关于 ε(h*) 的边界,有下列推论:
推论:对于所有的 h∈H,满足 |ε(h)-ε^(h)|≤γ,至少有 1-δ 的概率,使 m=Oγ,δ(d)。
换句话说,使用 H 能学好的训练集数目跟 H 的 VC 维是呈线性关系的,对于大多数假设类,VC 维也同参数个数大致呈线性关系。总而言之,对于一个最小化训练误差的算法,所需的训练集的数目通常跟 H 的参数个数呈线性关系。
参考资料:
1、http://cs229.stanford.edu/notes/cs229-notes4.pdf
2、http://blog.csdn.net/stdcoutzyx/article/details/18407259
