上回我们说到Expression Tree是一种表示编程语言中“表达式”概念的树状数据结构,并且学习了从Lambda表达式自动生成表达式树的C#语法。那么它到底有什么用呢?其实上一回已经提到了Expression Tree的基本功能:分析表达式的逻辑、保存和传输表达式以及重新编译表达式。现在我们就分别来看这三项基本功能如何使用。
分析表达式的逻辑
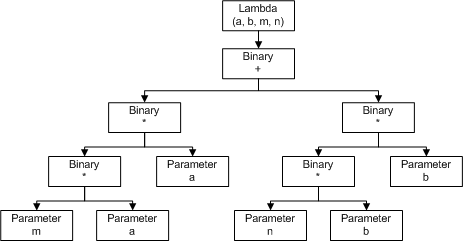
表达式树中已经包含了表达式所需的各种成分,我们只需要像遍历树一样遍历表达式树,就可以解析表达式的含义。我们现在就来动手解析一下四则运算的表达式树。假设表达式中仅有加减乘除运算。比方说我们有这个一个表达式(a, b, m, n) => m * a * a + n * b * b,它的表达式树是这样:
最外层是LambdaExpression,我们很容易就可以从它的Body属性得到里面的表达式。在限定条件下,这个表达式只含有BinaryExpression一种表达式。我们只需要要遍历这棵树,在遇到BinaryExpression的时候完成所需的运算即可。我们此处采用的是后序遍历的逻辑:
class Program { static void Main(string[] args) { Expression<Func<double, double, double, double, double>> myExp = (a, b, m, n) => m * a * a + n * b * b; var calc = new BinaryExpressionCalculator(myExp); Console.WriteLine(calc.Calculate(1, 2, 3, 4)); } } class BinaryExpressionCalculator { Dictionary<ParameterExpression, double> m_argDict; LambdaExpression m_exp; public BinaryExpressionCalculator(LambdaExpression exp) { m_exp = exp; } public double Calculate(params double[] args) { //从ExpressionExpression中提取参数,和传输的实参对应起来。 //生成的字典可以方便我们在后面查询参数的值 m_argDict = new Dictionary<ParameterExpression, double>(); for (int i = 0; i < m_exp.Parameters.Count; i++) { //就不检查数目和类型了,大家理解哈 m_argDict[m_exp.Parameters[i]] = args[i]; } //提取树根 Expression rootExp = m_exp.Body as Expression; //计算! return InternalCalc(rootExp); } double InternalCalc(Expression exp) { ConstantExpression cexp = exp as ConstantExpression; if (cexp != null) return (double)cexp.Value; ParameterExpression pexp = exp as ParameterExpression; if (pexp != null) { return m_argDict[pexp]; } BinaryExpression bexp = exp as BinaryExpression; if (bexp == null) throw new ArgumentException("不支持表达式的类型", "exp"); switch (bexp.NodeType) { case ExpressionType.Add: return InternalCalc(bexp.Left) + InternalCalc(bexp.Right); case ExpressionType.Divide: return InternalCalc(bexp.Left) / InternalCalc(bexp.Right); case ExpressionType.Multiply: return InternalCalc(bexp.Left) * InternalCalc(bexp.Right); case ExpressionType.Subtract: return InternalCalc(bexp.Left) - InternalCalc(bexp.Right); default: throw new ArgumentException("不支持表达式的类型", "exp"); } } } |
我们用了一个递归逻辑实现了遍历,为了方便封装了一个简单的类。这个简单的程序就可以计算任意double型参数的四则运算表达式。大家可能要问了,C#本身就具有运算四则运算表达式的能力,为什么我们要亲自解析表达式树来做到的同样的功能呢?如果仅仅是计算表达式的值,当然不用自己来解析。但自己解析的一大好处就是可以在解析过程中加入自定义的语义动作。比如我们只要稍微更改一下上述程序中的InternalCalc就能输出Lambda表达式的前缀序列:
string InternalPrefix(Expression exp) { ConstantExpression cexp = exp as ConstantExpression; if (cexp != null) return cexp.Value.ToString(); ParameterExpression pexp = exp as ParameterExpression; if (pexp != null) return pexp.Name; BinaryExpression bexp = exp as BinaryExpression; if (bexp == null) throw new ArgumentException("不支持表达式的类型", "exp"); switch (bexp.NodeType) { case ExpressionType.Add: return "+ " + InternalPrefix(bexp.Left) + " " + InternalPrefix(bexp.Right); case ExpressionType.Divide: return "- " + InternalPrefix(bexp.Left) + " " + InternalPrefix(bexp.Right); case ExpressionType.Multiply: return "* " + InternalPrefix(bexp.Left) + " " + InternalPrefix(bexp.Right); case ExpressionType.Subtract: return "/ " + InternalPrefix(bexp.Left) + " " + InternalPrefix(bexp.Right); default: throw new ArgumentException("不支持表达式的类型", "exp"); } } |
您可以尝试一下将自己的四则运算表达式转换成前缀序列是什么样子,有点函数式语言的味道了~ 我们还可以改变上述程序,让他实时输出四则运算的中间结果等。大家可以试验一下。
由此可见,我们分析表达式树并不一定是要计算表达式的值,我们可以在翻译表达式的时候执行任何自定义的语义动作,达到翻译表达式或用表达式驱动特殊代码的作用。Linq to Sql就是这个用途的典型例子。我们知道Linq to Sql的QueryProvider可以将IQueryable上的一系列查询动作翻译成SQL语句。那么表达式树是如何充当这个角色的呢?下面我们来看一个Queryable的例子:
IQueryable<double> source = ... var query = from d in source where d > 0 select d * 2; |
这个查询语句等价于如下直接使用Queryable扩展方法的代码:
var query = source.Where(d => d > 0).Select(d => d * 2); |
和Enumerable类型的扩展方法不同,Queryable扩展方法的每个操作都接受一个强类型的LambdaExpression参数。因此上述代码中的Where和Select分别接受了一个Expression Tree作为参数。最后的query对象中包含了整个序列每个操作对应的表达式树,QueryProvider就可以通过分析表达式树,翻译成SQL或者直接进行查询动作了。
这种用法有点类似于解释器模式。你可以用Expression Tree来表示一种逻辑,然后解析它来驱动你的业务逻辑。原本属于具体语言的表达式现在成为了我们可以直接利用的一大利器。
序列化和传输表达式
通过上文我们学习了解析表达式树并且执行自定义动作的方法。在实际应用中,我们还可能遇到以下需求:
1. 生成表达式的程序与解析表达式的程序不在同一进程内(例如在客户端生成表达式,在服务端解析)。
2. 需要储存或缓存表达式,为以后多次使用做准备。
3. 需要用其他非.NET技术处理或生成表达式树。
以上需求需要将表达式树当成纯数据来看待。内存中保存表达式树固然没有问题,我们还需要探究表达式树序列化的问题。
.NET 3.5版本的表达式树本身并没有特别优雅的序列化方式,它并不支持DataContract序列化。因为表达式的种类繁多,许多表达式都和CLR具体类型相关。通常的做法是,根据自己要使用的表达式子集手动编写序列化的代码。ToString()也可以得到一个表示表达式的字符串,可惜他不是那么容易变回表达式树。所以ToString()通常仅仅作为显示和参考。
MSDN Code Gallery中有一个LuckH提供的通用Expression Tree序列化例子。它可以提供比较清晰地XML序列化结果。
关于Expression Tree缓存,可以看老赵的这一系列文章,你可以学到各种利用表达式树自身特性的有趣用法。
习题
1. 基于本文提供的四则运算例子,给他加上支持一元正负运算符和函数调用的功能。这样你就能计算Math.Sin(a) + b这样的表达式了。可以先仅支持静态函数。
2. 改写这个程序,使之能根据四则运算表达式树生成javascript代码。
3. 你可以试着将以上代码扩展成一个小小的类库,能用javascript来执行你提供的四则运算表达式。
(待续)