1014

A.三角形
问题描述
给你一个尺寸为(n imes m)的字符矩阵，请你找出矩阵中所有的“字同三角形”。

所谓“字同三角形”是指由至少三个相同字符构成的“等腰直角三角形”，且直角边与矩阵的边平行。例如：下图矩阵中，含有7个“字同三角形”。

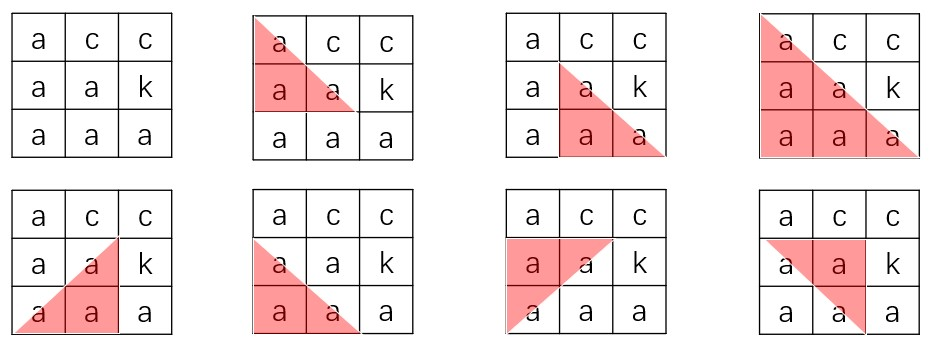
最开始想的有点小偏 以为是(dfs)求联通块
然后发现一些性质好像可以用动态规划来解决
然后我就定义了一个三维的数组
定义 (f[i][j][k])表示 在 以((i,j)) 为结尾的是否能够构成直角边长长度为k
假如我们分四种情况来讨论直角三角形的情况
我们有状态转移方程 这里只列举一种

(ans+=(f[i][j][s+1]==f[i-1][j-1][s]);)

然后就可以利用滚动数组优化掉空间
然后我TLE 44...

回去和某位巨佬谈论了一下 发现我的做法可以再优化一下 原因是多了一个k 动态规划怎么能没有决策呢??
(f[i][j])表示((i,j)) 能够贡献的最大的高度
称为三角形的充要条件是(i,j)的上一层最多能成为的高度和能够对 ((i,j))点对贡献它的高度个三角形 条件是((i,j))前面已经有了这么多能够达成的边长
然后我们就可以 得到状态转移方程
当然还可以枚举直角边

	f[i][j]=min(ff[j]-1,f[i-1][j-1])+1;
	ans+=f[i][j]-1;

code:

//
#include<bits/stdc++.h>
using namespace std;
#define maxnn 2005
int n,m;
char ch[maxnn][maxnn];
int f[maxnn][maxnn];
int f2[maxnn][maxnn];
int ff[maxnn];
int k=1;
int ans=0;
void FIE() {
	freopen("triangie.in","r",stdin);
	freopen("triangie.out","w",stdout);
}
int main() {
	//FIE();
	cin>>n>>m;
	for(int i=1; i<=n; i++) {
		scanf("%s",ch[i]+1);
	}
	//case 1
	for(int i=1; i<=n; i++) {
		for(int j=0; j<=m; j++) {
				f[i][j]=0;
		}
	}
	for(int i=1; i<=n; i++) {
		for(int j=1; j<=m; j++) {
			ff[j]=1;
			f[i][j]=1;
		}
		for(int j=1; j<=m; j++) {
			if(ch[i][j-1]==ch[i][j]) {
				ff[j]=ff[j-1]+1;
			}
			if(ch[i-1][j-1]==ch[i][j]) {
			 {
					{
						f[i][j]=min(ff[j]-1,f[i-1][j-1])+1;
						ans+=f[i][j]-1;
					}
				}
			}
		}
	}
	//case2

	for(int i=1; i<=n; i++) {
		for(int j=1; j<=m; j++) {
				f[i][j]=0;
		}
	}
	for(int i=1; i<=n; i++) {
		for(int j=1; j<=m; j++) {
			ff[j]=1;
			f[i][j]=1;
		}
		for(int j=m; j>=1; j--) {
			if(ch[i][j+1]==ch[i][j]) {
				ff[j]=ff[j+1]+1;
			}
			if(ch[i-1][j+1]==ch[i][j]) {
			 {
					f[i][j]=min(ff[j]-1,f[i-1][j+1])+1;
					ans+=f[i][j]-1;
				}
			}
		}
	}
	//case 3

	for(int i=1; i<=n; i++) {
		for(int j=1; j<=m; j++) {
				f[i][j]=0;
				f[i][j]=1;
		}
	}
	for(int i=n; i>=1; i--) {
		for(int j=1; j<=m; j++) {
			ff[j]=1;
		}

		for(int j=m; j>=1; j--) {
			if(ch[i][j+1]==ch[i][j]) {
				ff[j]=ff[j+1]+1;
			}
			if(ch[i+1][j+1]==ch[i][j]) {
			 {
					f[i][j]=min(ff[j]-1,f[i+1][j+1])+1;
						ans+=f[i][j]-1;
				}
			}
		}
	}
	//case 4
	for(int i=1; i<=n; i++) {
		for(int j=1; j<=m; j++) {
				f[i][j]=0;
				f[i][j]=1;
		}
	}
	for(int i=n; i>=1; i--) {
		for(int j=1; j<=m; j++) {
			ff[j]=1;
		}
		for(int j=1; j<=m; j++) {
			if(ch[i][j-1]==ch[i][j]) {
				ff[j]=ff[j-1]+1;
			}
			if(ch[i+1][j-1]==ch[i][j]) {
			 {
			 {
					f[i][j]=min(ff[j]-1,f[i+1][j-1])+1;
						ans+=f[i][j]-1;
				}
			}

			}
		}
	}
	cout<<ans;
}