NOIP模拟题 栅栏

题目大意

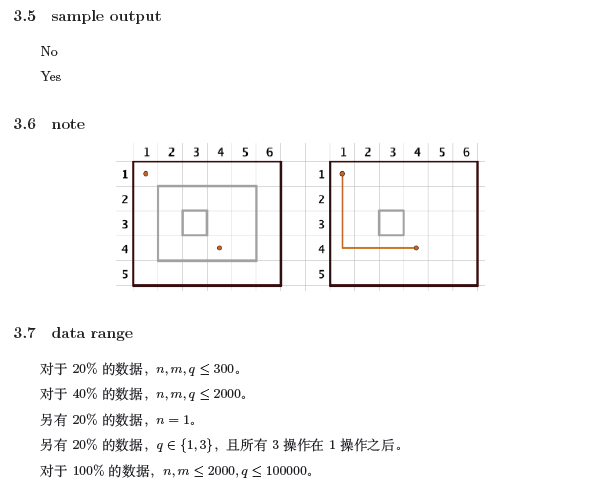
给定一个$n imes m$的网格图，每次会选择一块矩形沿着网格线铺上栅栏，或者拆除之前铺的栅栏，或者询问两个格子能否不经过栅栏直接到达。

保证栅栏没有重叠或交叉，删去的栅栏删除前一定存在。

题解

考虑两个格子能互相到达，当且仅当包含它们的栅栏完全相同。考虑对每一个栅栏随机一个权值，维护覆盖每个点的所有栅栏的异或和。

询问两个点时，若两个点权值不相同，那么一定不在。否则，可以直接认为覆盖它们的栅栏集合完全相同。

由于在$MaxInt$范围内随机权值，那么一共会出现$2^30$种权值异或和，几乎已经不可能出现重合。也可以用多次随机和扩大权值范围来增大正确率。

至于矩形异或，维护一个点的权值，可以直接使用差分$+$二维树状数组。

复杂度$O(Qlog nlog m)$。

#include<bits/stdc++.h>
#define debug(x) cerr<<#x<<" = "<<x
#define sp <<"  "
#define el <<endl
#define LL long long
#define N 2020
#define M 100020
#define pii pair<int,int>
#define mp make_pair
using namespace std;
int read(){
	int nm=0,fh=1; char cw=getchar();
	for(;!isdigit(cw);cw=getchar()) if(cw=='-') fh=-fh;
	for(;isdigit(cw);cw=getchar()) nm=nm*10+(cw-'0');
	return nm*fh;
}
int n,m,nt[M],bf[M],tot,c[N][N],p[M]; map<pii,int> MP;
int rd(){return (rand()<<13)^rand();}
inline void ins(int x,int y,LL dt){
	for(int k1=x;k1<=n;k1=nt[k1]) for(int k2=y;k2<=m;k2=nt[k2]) c[k1][k2]^=dt;
}
inline LL qry(int x,int y){
	LL tt=0;
	for(int k1=x;k1;k1=bf[k1]) for(int k2=y;k2;k2=bf[k2]) tt^=c[k1][k2];
	return tt;
}
#define add(x,y,xx,yy,dt) ins(x,y,dt),ins(x,yy+1,dt),ins(xx+1,y,dt),ins(xx+1,yy+1,dt)
int main(){
	srand(19260817); n=read(),m=read();
	for(int i=1;i<=max(n,m);i++) nt[i]=i+(i&-i),bf[i]=i-(i&-i);
	for(int tpe,t1,t2,t3,t4,id,T=read();T;T--){
		tpe=read(),t1=read(),t2=read(),t3=read(),t4=read();
		if(tpe==1){MP[mp(t1,t2)]=++tot,p[tot]=rd(),add(t1,t2,t3,t4,p[tot]);}
		else if(tpe==2){id=MP[mp(t1,t2)];add(t1,t2,t3,t4,p[id]);}
		else{bool fg=(qry(t1,t2)==qry(t3,t4));puts(fg?"Yes":"No");}
	}
	return 0;
}