题目描述
组合数Cmn表示的是从n个物品中选出m个物品的方案数。举个例子,从(1,2,3) 三个物品中选择两个物品可以有(1,2),(1,3),(2,3)这三种选择方法。根据组合数的定 义,我们可以给出计算组合数的一般公式:
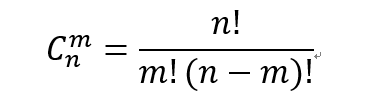
其中n! = 1 × 2 × · · · × n
小葱想知道如果给定n,m和k,对于所有的0 <= i <= n,0 <= j <= min(i,m)有多少对 (i,j)满足Cji是k的倍数。
输入输出格式
输入格式:
第一行有两个整数t,k,其中t代表该测试点总共有多少组测试数据,k的意义见 【问题描述】。
接下来t行每行两个整数n,m,其中n,m的意义见【问题描述】。
输出格式:
t行,每行一个整数代表答案。
算法分析
暴力求组合数,暴力求有多少组合数模k等于0
要知道的是组合数的递推公式
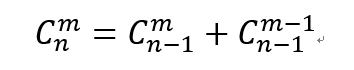
和矩阵前缀和怎么求
但是这道题为什么能卡一下午呢
因为我在用组合数的时候习惯把m作为较大的那个数(。。),然后又搞不清楚i和j对应n还是m还有对应行还是列(。。。。),其实很好理解。
代码
1 #include<bits/stdc++.h> 2 using namespace std; 3 int c[2010][2010],s[2010][2010],n[10010],m[10010]; 4 int main(){ 5 int t,k; 6 scanf("%d%d",&t,&k); 7 int maxn=0,maxm=0; 8 for (int i=1; i<=t; i++){ 9 scanf("%d%d",&n[i],&m[i]); 10 maxn=max(maxn,n[i]); 11 maxm=max(maxm,m[i]); 12 } 13 for (int i=0; i<=maxn; i++) c[i][0]=1;//初始化 14 for (int i=1; i<=maxn; i++) 15 for (int j=1; j<=maxm; j++){ 16 c[i][j]=(c[i-1][j]+c[i-1][j-1])%k;//组合数公式 17 if (!c[i][j]&&i>=j) s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+1;//矩阵前缀和 18 else s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]; 19 } 20 for (int i=1; i<=t; i++) 21 printf("%d ",s[n[i]][m[i]]); 22 return 0; 23 }