·大米兔学习全排列,还有一些逆序对,还有一棵二叉索引树。·
·分析:
首先肯定不是像题目上说的那样,使用next_permutation去完成这道题,因为就算是线性的它也不能承受庞大的排列组合个数。
我们发现这道题可以理解为:建造一个字典序尽量小的序列,满足:①字典序大于原序列②逆序数等于原数列。
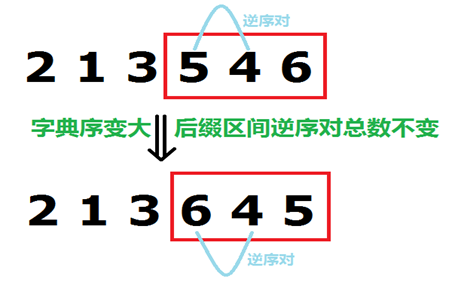
怎样才能满足字典序最小呢?首先,我们视作从原数列去修改得到我们的美妙新序列。为了使得新序列字典序尽量靠近原序列(这样才是答案),我们更愿意去修改靠近尾部的部分,这样字典序变换较小。如图:
转换一种思想:我们将要改变原序列的部分规定为原序列的一个后缀,也就是说啊,在这之前的部分我们不作更改,并且改变后这一段的逆序对数目不发生改变。如图啦啦:
那么为什么修改段尽量靠后就一定是答案呢?因为如果靠前一点,如果后面段已经存在解了,那么较长的后缀里构造出来的数列的字典序一定大于等于较短一段。因此,我们需要寻找满足条件的最短后缀,找到以后,对调整它内部元素的顺序,构成答案。
照此思路,必有两个步骤:①找到这个后缀是谁(代码中可以体现为找到后缀左端点)②调整这个区间内的元素顺序,构造答案。
(1)寻找那个梦中的后缀:
不是所有的短后缀都能通过仅修改它内部的元素构造最终答案。我们观赏以下情况,为了方便理解;
我们用柱柱的高度表示每个元素的大小,红色部分表示我们选择这一段后缀来修改,设i为后缀的左端点下标,使用now表示当前数i在区间[i,n]的逆序对数(也就是在这个后缀中关于i的逆序对个数),使用sum表示这个后缀中的总逆序对数[一句提醒:i之前的逆序对我们是不会理睬它的]。我们在草稿纸上乱涂乱画,轻松发现下列情况是不合法的(即仅选择这一段后缀进行修改是不能达到目的的):
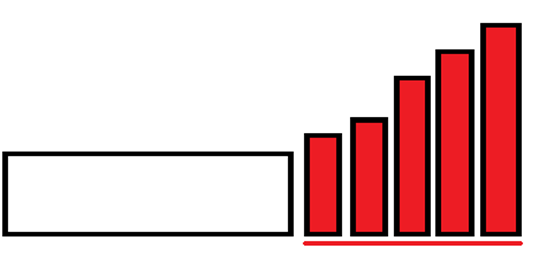
【1】单调上升型:
由于后缀区间里的逆序对个数为0,所以我们不可能仅通过调整红色部分内部的元素顺序来保持原来的逆序对总数。这种情况的判断方式为:sum==0。
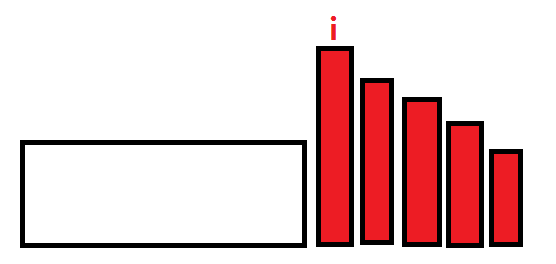
【2】单调递减型
这种情况的不合法的原因和上文类似。由于逆序对数已经达到了这个区间的唯一最大值:(n-i)*(n-i+1),不可能有其他排列方式。这种情况的判断方式为:sum==(n-i)*(n-i+1)。
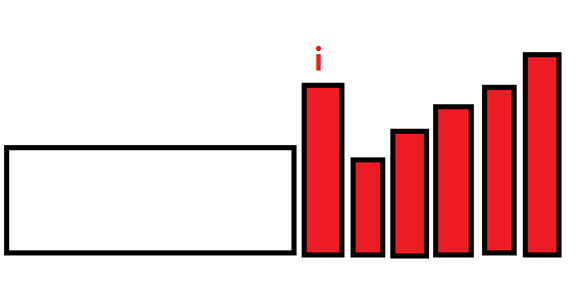
【3】垄断型:
此时后缀区间内的所有逆序对都是与i相关的,即sum==now。由于我们要构造字典序更大的一个后缀,那么只能把i位置放上比a[i]大的元素(例如图中的最后一个元素),这个元素一放过来,那么必定会至少造成now+1个逆序对(就是原来i的逆序对和它与i组成的逆序对)。
上文几个自然段已经列出了判断条件,这让我们可以快乐而顺利地从右向左找到第一个合法的后缀i。接下来就要努力构造答案了。
(2)在那个后缀中建造我们的梦:
对于第I位(也就是这个后缀区间的左端点),我们需要保证这一位要换成一个比原来的a[i]大的,但值又尽量小的元素。我们有i的now值可以得到:
在这个后缀区间中,i是第(now+1)小,所以我们为保证新序列字典序尽量小,把i位替换成这个序列第(now+2)大的数(注意,不是整个序列第几大,是这个后缀中的第几大,怎么找到它呢,一会儿说好吗?好)。其实接下来处理完i位后,我们依次处理i+1~n位的方法大体相同:
方法为:我们要尽力使得这个序列字典序最小。啊?这是什么方法啊。欣赏下面这幅图:
我们要坚持让j位元素尽量小的原则(在这之前的部分已经填好数),要让这个数尽量小,也就是它的和剩余区间的逆序对要尽量少,那么在总逆序对保持不变的情况下(这是关键),那么就要使[j+1,n]内部的逆序对尽量多,我们考虑最极端情况,也就是[j+1,n]部分直接呈现单调递减型,那么这样逆序对最大,使得关于j的逆序对最小,使得j位的数最小。
①②整个过程思路如下:
从右向左扫描,找到第一个通过修改能够构成满足条件的字典序最小的新序列的后缀。然后从左向右扫描,保持当前处理的区间[j,n]的逆序对不变,合理分配逆序对的来源,使得关于j的逆序对最少,从而保证最终构造出来的序列的字典序接近原序列。
代码实现算法推荐:今天树状数组半价,推荐您使用这一款。它的这三个操作可以完全胜任这道题:
find函数当然是用来找到第k大的啦。
调用刘汝佳老师经常说的一句话:“本题非常经典,代码实现还有很多细节,请读者认真思考,强烈建议上机实践。(想一想,为什么)”
1 #include<stdio.h> 2 #include<algorithm> 3 #define ll long long 4 #define go(i,a,b) for(int i=a;i<=b;i++) 5 #define ro(i,a,b) for(int i=a;i>=b;i--) 6 using namespace std; 7 int n,a[1200010],c[1200010],s,S=1;ll now,sum; 8 void ADD(int x,int d){while(x<=S)c[x]+=d,x+=x&-x;} 9 int Sum(int x){int R=0;while(x)R+=c[x],x-=x&-x;return R;} 10 int find(int x){s=S;while(s)c[x+s]<now?x+=s,now-=c[x]:1,s>>=1;return x;} 11 int main() 12 { 13 scanf("%d",&n);while(S<=n)S<<=1; 14 go(i,1,n)scanf("%d",a+i); 15 ro(I,n,1) 16 { 17 sum+=(now=Sum(a[I]));ADD(a[I],1); 18 if(now<sum&&now<n-I&&sum<1ll*(n-I+1)*(n-I)/2) 19 go(i,I,n)i==I?now++:now=max(1ll*0,sum-1ll*(n-i)*(n-i-1)/2), 20 sum-=now++,ADD(a[i]=find(0)+1,-1),I=1; 21 } 22 go(i,1,n)printf("%d ",a[i]);puts("");return 0; 23 }//Paul_Guderian
这是我们的梦,一个真实的梦,
让每个人和每颗心紧紧相拥。—————汪峰《我们的梦》