转载自:http://blog.csdn.net/fengchaokobe/article/details/7437767
第一节 n阶幻方问题
第二节 由n阶幻方引发的思考
正文
第一节 n阶幻方问题
所谓n阶幻方问题,俗称“横竖斜相加和相等”(我们当时就是这么叫的)。用术语说就是:在一个N行N列的方格表中,有1,2,3......N*N-1,N*N这N*N个整数,且其对角线、横行、纵行的数字和都相等。
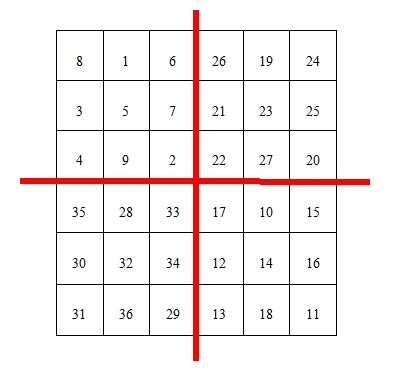
好了,在具体详解该问题之前,我们先看个例子,熟悉一下,如下图所示:

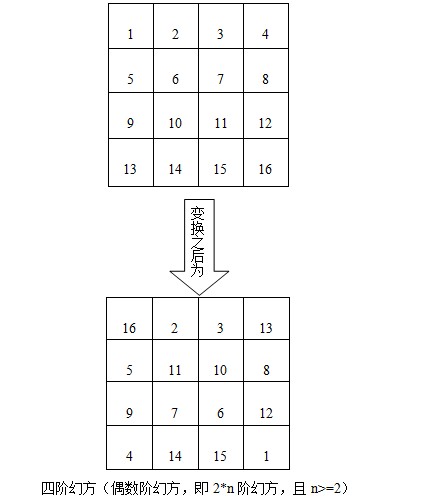
1.奇数阶幻方
我记得基数阶幻方有个口诀,有了这个口诀,走遍奇数幻方都不怕。其实这个口诀也是实现奇数幻方的步骤。
先填上行正中央,
依次斜填切莫忘。
上格没有顶格填,
顶格没有底格放。
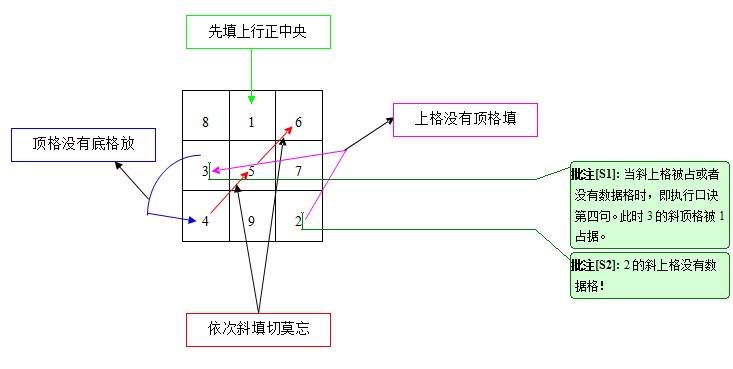
附注:如果上述口诀有什么问题,请留言说明,谢谢!
注:按我的理解就是在第一行中间填数字1,然后依次向左上角填写数字2,3,4。。。。如果当前数字的左上角已经被占用,那么就在当前数字的下方填写,再依次向左上角按顺序填写
ok,奇数幻方就讲完了,就这么简单。权当找乐子!
2.偶数阶幻方
说实话,偶数阶幻方我一直以为只有一种,就是2*n阶幻方问题。查了一下才知道偶数阶幻方也分为两小类。
①.4*n阶幻方
4*n阶幻方的生成其实很简单,即对方格中对角线上的数据,先以一条对角线(称对角线一)为对称轴,交换另一对角线(称对角线二)的数据;然后以对角线二为对称轴,交换对角线一的数据。说的直白一点,假设矩阵名为MagicSquare,就是交换MagicSquare[i,j]和MagicSquare[n-1-i,n-1-j]。老办法,作图来说明。图如下:

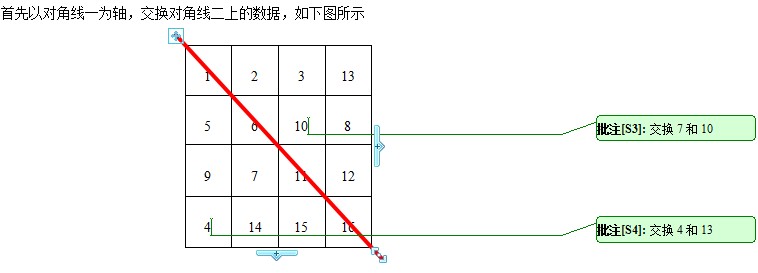

②.4*n+2阶幻方
4*n+2,乍一看就较4*n麻烦了,事实也是如此,不过它的思想也简单。就是将4*n+2看做2*(2*n+1),这样一来就转化成了四个2*n+1求幻方。
附注:下面的我以6阶幻方为例,那么,4*n+2=6,所以n=1。
我通过描述每个步骤加上图形的方式来表述4*n+2阶幻方实现的过程。
第一步:把整个表格分成4个(2*n+1)*(2*n+1)的小表格,分别叫A,B,C,D。见下图
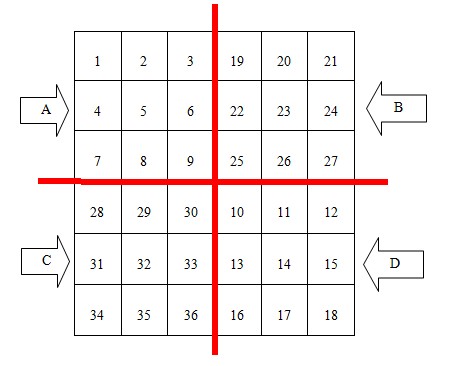
第二步:这样A,B,C,D个小表格就成奇数幻方问题了。
①.将1,2,...,(2*n+1)*(2*n+1)这些数划分给A,并对A实现奇数幻方;
②.将(2*n+1)*(2*n+1)+1,...,2*(2*n+1)*(2*n+1)这些数划分给B,并对B实现奇数幻方;
③.将2*(2*n+1)*(2*n+1)+1,...3*(2*n+1)*(2*n+1)这些数划分C,并对C实现奇数幻方;
④.将3*(2*n+1)*(2*n+1)+1,...4*(2*n+1)*(2*n+1)这些数划分D,并对D实现奇数幻方。
见下图
第三步:从A表中的中心(即第n行的MagicSquare[n][n])开始,按照从左向右的方向,标出n个数,A表中的其他行则标出最左边的n格中的数(在图中用红色背景标出)。并且将这些标出的数和C表中的对应位置互换。见下图
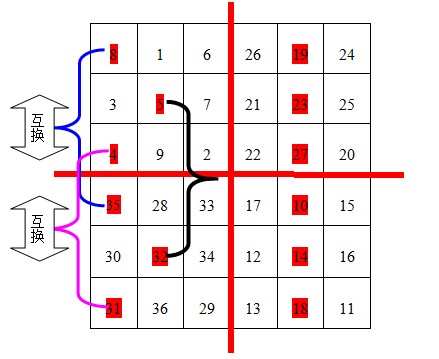
第四步:在B表中的中心(如上解释)开始,自右向左,标出n-1列,将B中标出的数据与D表中对应位置的数据交换。但是6阶幻方中,n-1此时等于0,所以B与D不用做交换。
至此,这个幻方就成了,如下图。
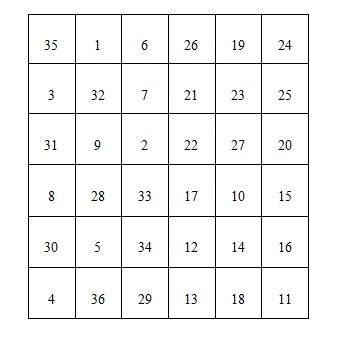
附注:以上几个问题的程序就不送上了,有兴趣的朋友可以自己写一下。
第二节 由n阶幻方想到的
幻方问题就说完了,比较一下我还是感觉奇数阶幻方有意思,而且比偶数阶幻方问题容易些,没有那么麻烦。按说写到此本应该结束了,可是我突发奇想,n阶幻方这个问题利用数学知识很容就能解决,那么我想问一下大家:在平时写程序思考算法的时候,你是否会利用数学知识来解决问题呢?
假如这个问题让你在限定的时间内编程来实现.如果你对n阶幻方很了解,知道奇偶两种情况的做法,好,那没有问题,恭喜你!但是,恰巧你对n阶幻方不是很了解,也不知道奇偶阶幻方的做法,那这个问题你会怎么解决?用枚举还是用其他什么算法。这是你不得不考虑的。
说到这,我又想到了一个例子,如:求1,2,...,99,100的和,请编程实现。你会怎么做?这个确实很简单,我相信多数朋友都会用一个for或是一个while来解决问题。那还有没有更简单的办法呢?当然有,利用数学知识来解决,1,2,...,99,100就是一个等差数列,等差数列求和的公式S=(首项+末项)*项数/2,直接得出结果。哪个效率更高,不言而喻。所以说,数学知识在我们编程中很有用,只是我们经常考虑不到而已!
第三节 结束语
如果你有更有趣或者值得深思的题目请分享!