using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using Microsoft.Practices.EnterpriseLibrary.Validation.Validators;
using Microsoft.Practices.EnterpriseLibrary.Validation;
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args) {
int[] arr = new int[] {10,5,3,6,8,9,7};
int[] recode = new int[arr.Length];
recode[0] = 1;
//求数组中最长非降 子序列
for (int i = 1; i < arr.Length; i++)
{
if (arr[i] > arr[i - 1])
recode[i] = recode[i-1]+1;
else
recode[i] = recode[i-1];
}
for (int i = 0; i < recode.Length ; i++)
{
Console.WriteLine("到第"+(i+1)+"元素的最长非降 子序列长度:"+recode[i]);
}
Console.Read();
}
}
}
执行结果 :这里保存了到某个长度下的所有状态 如果不需要 完全可以用int变量存储 不需要使用数组 这样复杂度分别为 o(n),o(1)
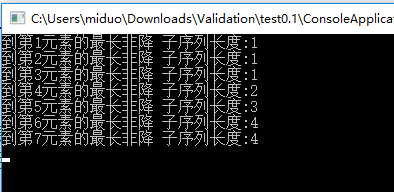
问题
一个序列有N个数:A[1],A[2],…,A[N],求出最长非降子序列的长度
分析 我先用列举法考虑简单情况 然后找规律
第一个元素最长非降序列长度肯定为1 因为只有本身 没有比较对象 记为 f(1)=1
到第二个元素 与第一个元素进行对比 如果小于第一个元素 那么这里第二个元素并没有为长度做出贡献 状态还保持在上一个元素 记 f(2)=1=f(1)
以此类推
最后得到以上结果
这是我对动态规划的入门理解 即之前最优的状态影响着当前状态 而上一个状态就是在这之前的最优状态 这样也能降低算法的复杂程度
第二例

代码
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using Microsoft.Practices.EnterpriseLibrary.Validation.Validators;
using Microsoft.Practices.EnterpriseLibrary.Validation;
namespace ConsoleApplication1
{
public class NodeDistance
{
/// <summary>
/// 节点名称
/// </summary>
public string nodeName { get; set; }
/// <summary>
/// 能到达的节点及与他们的距离列表
/// </summary>
public List<(string nodeName, int distance)> distance { get; set; }
}
class Program
{
//记录已到达的(走到当前的)最短路径
static (string lujin, int distance) luxianDaoDa = ("", int.MaxValue);
static void Main(string[] args)
{
// 问题 无向图上有N(1<N)个节点 每个节点有任意长的距离 计算任意节点A到任意节点B的距离
//使用二维数组模拟点的情况 以及单个点到其他点的距离 先从简单的情况开始考虑 有abcd四个节点 每个节点可以到达其他节点
List<NodeDistance> nodeList = new List<NodeDistance>() {
new NodeDistance
{
nodeName="a",
distance=new List<(string nodeName, int distance)>{
("b",2),("c",7),("c",7)
}
},
new NodeDistance
{
nodeName="b",
distance=new List<(string nodeName, int distance)>{
("a",2),("c",3),("d",2)
}
},
new NodeDistance
{
nodeName="c",
distance=new List<(string nodeName, int distance)>{
("a",7),("d",5),("b",3)
}
},
new NodeDistance
{
nodeName="d",
distance=new List<(string nodeName, int distance)>{
("a",6),("c",3),("b",2)
}
},
};
List<(string lujin, int distance)> luxian = new List<(string lujin, int distance)>();
//求a-c得最短路径
CalcDistance("a", "c", "a", 0, nodeList);
Console.WriteLine("最短路径:" + luxianDaoDa.lujin + "距离为:" + luxianDaoDa.distance);
Console.Read();
}
/// <summary>
/// 计算距离
/// </summary>
/// <param name="node">当前节点</param>
/// <param name="endChar">结束位置</param>
public static void CalcDistance(string startChar, string endChar, string luxianName, int distance, List<NodeDistance> nodeList)
{
var node = nodeList.Where(u => u.nodeName == startChar).FirstOrDefault();
//记录走过的节点
foreach (var item in node.distance)
{
//判断当前节点是否走过 或者是否为起点
if (item.nodeName == "a") continue;
luxianName += item.nodeName;
// 判断是否为当前情况下的最优状态 如果是 判断是否为终点
distance += item.distance;
if (distance >= luxianDaoDa.distance) continue;
if (item.nodeName == endChar)
luxianDaoDa = (luxianName, distance);
else
CalcDistance(item.nodeName
, endChar, luxianName, distance, nodeList);
}
}
}
}
运行结果
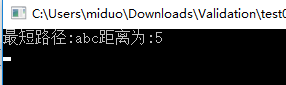
抽屉取苹果
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using Microsoft.Practices.EnterpriseLibrary.Validation.Validators;
using Microsoft.Practices.EnterpriseLibrary.Validation;
namespace ConsoleApplication1
{
class Program
{
static int[][] apple = new int[3][];
static int[][] appleSum = new int[3][];
static void Main(string[] args) {
apple[0] = new int[] {3,2,4};
apple[1] = new int[] { 2,1,3 };
apple[2] = new int[] { 6,5,1};
appleSum[0] = new int[apple[0].Length];
appleSum[1] = new int[apple[0].Length];
appleSum[2] = new int[apple[0].Length];
appleSum[0][0] = apple[0][0];//初始只能取到本身
//先填充第一行与第一列
for (int i = 1; i < apple.Length; i++)
{
appleSum[0][i] = appleSum[0][i - 1] + apple[0][i];
appleSum[i][0] = appleSum[i-1][0] + apple[i][0];
}
//当前位置记为array[x][y] 然后填充其他行与列 值为max(array[x+1][y],array[x][y+1])
for (int x = 1; x < apple.Length; x++)
for (int y = 1; y < apple[0].Length; y++)
appleSum[x][y]= (appleSum[x - 1][y] > appleSum[x][y - 1] ? appleSum[x - 1][y] : appleSum[x][y - 1])+apple[x][y];
Console.WriteLine("最大值:"+appleSum[apple.Length-1][apple[0].Length-1]);
Console.Read();
}
}
}
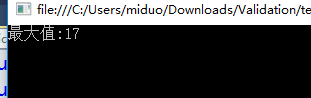
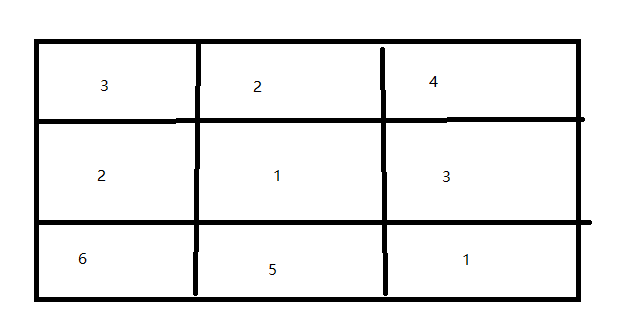
具体分析 http://www.cnblogs.com/lihonglin2016/p/4298432.html