//第一次在新博客里发文章好紧张怎么办
//MD巨神早已在一个小时前做完了
The Rotation Game
| Time Limit: 15000MS | Memory Limit: 150000K | |
| Total Submissions: 5950 | Accepted: 1992 |
Description
The rotation game uses a # shaped board, which can hold 24 pieces of square blocks (see Fig.1). The blocks are marked with symbols 1, 2 and 3, with exactly 8 pieces of each kind.
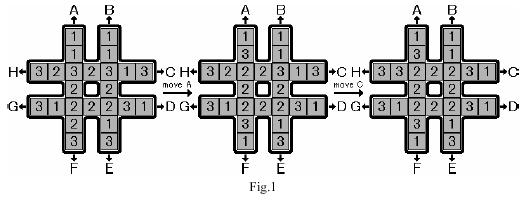
Initially, the blocks are placed on the board randomly. Your task is to move the blocks so that the eight blocks placed in the center square have the same symbol marked. There is only one type of valid move, which is to rotate one of the four lines, each consisting of seven blocks. That is, six blocks in the line are moved towards the head by one block and the head block is moved to the end of the line. The eight possible moves are marked with capital letters A to H. Figure 1 illustrates two consecutive moves, move A and move C from some initial configuration.

Initially, the blocks are placed on the board randomly. Your task is to move the blocks so that the eight blocks placed in the center square have the same symbol marked. There is only one type of valid move, which is to rotate one of the four lines, each consisting of seven blocks. That is, six blocks in the line are moved towards the head by one block and the head block is moved to the end of the line. The eight possible moves are marked with capital letters A to H. Figure 1 illustrates two consecutive moves, move A and move C from some initial configuration.
Input
The input consists of no more than 30 test cases. Each test case has only one line that contains 24 numbers, which are the symbols of the blocks in the initial configuration. The rows of blocks are listed from top to bottom. For each row the blocks are listed from left to right. The numbers are separated by spaces. For example, the first test case in the sample input corresponds to the initial configuration in Fig.1. There are no blank lines between cases. There is a line containing a single `0' after the last test case that ends the input.
Output
For each test case, you must output two lines. The first line contains all the moves needed to reach the final configuration. Each move is a letter, ranging from `A' to `H', and there should not be any spaces between the letters in the line. If no moves are needed, output `No moves needed' instead. In the second line, you must output the symbol of the blocks in the center square after these moves. If there are several possible solutions, you must output the one that uses the least number of moves. If there is still more than one possible solution, you must output the solution that is smallest in dictionary order for the letters of the moves. There is no need to output blank lines between cases.
Sample Input
1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3
1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3
0
Sample Output
AC
2
DDHH
2
------------------------------------------------------------------------------------------------------
poj英文题的尿性呵呵哒
大概就是把那个棋盘的abcdef轴旋转次数最少使得中间那几个数字相同(注意只有1,2,3)
那么先找规律,就是把输入数据的位置与abcdef对应
接下来因为搜索层数未知,dfs会TLE,bfs会MLE,所以容易想到ID搜索
先指定递归层数,然后迭代加深一层一层搜下去(有的说用二分但这种小数据反而更费时)
再看每一层的搜索方向
联想八数码问题(然而并不清楚八数码问题),发现每个状态都有最多递归的层数(八个位置贪心减去目前最多的数字个数)
那么写一个估价函数猜猜最多搜多少,如果超出了层数限制那就剪枝,这样就有了IDA*
(我在说些什么)
代码代码代码我要去睡
1 #include<stdio.h>
2 #include<stdlib.h>
3 #include<string.h>
4 #include<limits.h>
5 int min(int a,int b){
6 return a<b?a:b;
7 }
8 int lines[10][10]={
9 { 0, 2, 6,11,15,20,22},// A
10 { 1, 3, 8,12,17,21,23},// B
11 {10, 9, 8, 7, 6, 5, 4},// C
12 {19,18,17,16,15,14,13},// D
13 {23,21,17,12, 8, 3, 1},//E
14 {22,20,15,11, 6, 2, 0},//F
15 {13,14,15,16,17,18,19},//G
16 { 4, 5, 6, 7, 8, 9,10},//H
17 };
18 int matrix[10]={6,7,8,11,12,15,16,17};
19 int cross[30];
20 char ans[100];
21 int check(){
22 for(int i=0;i<8;i++)if(cross[matrix[0]]!=cross[matrix[i]])return 0;
23 return 1;
24 }
25 int predict(){
26 int most=100;
27 for(int i=1;i<=3;i++){
28 int a=0;
29 for(int j=0;j<8;j++)if(cross[matrix[j]]!=i)a++;
30 most=min(most,a);
31 }
32 return most;
33 }
34 int rotate(int mode){
35 int le=cross[lines[mode][0]];
36 for(int i=0;i<6;i++)cross[lines[mode][i]]=cross[lines[mode][i+1]];
37 cross[lines[mode][6]]=le;
38 return 0;
39 }
40 int dfs(int dpt,int dptm){
41 if(dpt==dptm) return check();
42 if(dpt+predict()>dptm) return 0;
43 for(int i=0;i<8;i++){
44 ans[dpt]=i+'A';
45 rotate(i);
46 if(dfs(dpt+1,dptm)) return 1;
47 if(i%2==0) rotate((i+5)%8);
48 else rotate((i+3)%8);
49 }
50 return 0;
51 }
52 int main(){
53 while(scanf("%d",&cross[0])!=EOF&&cross[0]!=0){
54 for(int i=1;i<24;i++) scanf("%d",&cross[i]);
55 if(check()) printf("No moves needed ");
56 else{
57 int i=0;
58 while(++i) if(dfs(0,i)) break;
59 ans[i]='�';
60 printf("%s ",ans);
61 }
62 printf("%d ",cross[matrix[0]]);
63 }
64 return 0;
65 }