小学生都能看懂的FFT！！！

小学生都能看懂的FFT！！！

---

前言

在创新实践中心偷偷看了一天FFT资料后，我终于看懂了一点。为了给大家提供一份简单易懂的学习资料，同时也方便自己以后复习，我决定动手写这份学习笔记。

食用指南：
本篇受众：如标题所示，另外也面向同我一样高中起步且非常菜的OIer。真正的dalao请无视。
本篇目标：让大家（和不知道什么时候把FFT忘了的我）在没有数学基础的情况下，以最快的速度了解并 会写 FFT。因此本篇将采用尽可能通俗易懂的语言，且略过大部分数学证明，在严谨性上可能有欠缺。但如果您发现了较大的逻辑漏洞，欢迎在评论里指正！

最后……来个版权声明吧。本文作者胡小兔，博客地址http://rabbithu.cnblogs.com。暂未许可在任何其他平台转载。

你一定听说过FFT，它的高逼格名字让人望而却步——“快速傅里叶变换”。
你可能知道它可以(O(n log n))求高精度乘法，你想学，可是面对一堆公式，你无从下手。
那么欢迎阅读这篇教程！

[Warning] 本文涉及复数（虚数）的一小部分内容，这可能是最难的部分，但只要看下去也不是非常难，请不要看到它就中途退出啊QAQ。

什么是FFT？

快速傅里叶变换（FFT）是一种能在(O(n log n))的时间内将一个多项式转换成它的点值表示的算法。

补充资料：什么是点值表示

设(A(x))是一个(n - 1)次多项式，那么把(n)个不同的(x)代入，会得到(n)个(y)。这(n)对((x, y))唯一确定了该多项式，即只有一个多项式能同时满足“代入这些(x)，得到的分别是这些(y)”。
由多项式可以求出其点值表示，而由点值表示也可以求出多项式。

（并不想证明，十分想看证明的同学请前往“参考资料”部分）。

注：下文如果不加特殊说明，默认所有(n)为2的整数次幂。如果一个多项式次数不是2的整数次幂，可以在后面补0。

为什么要使用FFT？

FFT可以用来加速多项式乘法（平时非常常用的高精度大整数乘法就是最终把(x = 10)代入的多项式乘法）。

假设有两个(n-1)次多项式(A(x))和(B(x))，我们的目标是——把它们乘起来。

普通的多项式乘法是(O(n^2))的——我们要枚举(A(x))中的每一项，分别与(B(x))中的每一项相乘，来得到一个新的多项式(C(x))。

但有趣的是，两个用点值表示的多项式相乘，复杂度是(O(n))的！具体方法：(C(x_i) = A(x_i) imes B(x_i))，所以(O(n))枚举(x_i)即可。

要是我们把两个多项式转换成点值表示，再相乘，再把新的点值表示转换成多项式岂不就可以(O(n))解决多项式乘法了！

……很遗憾，显然，把多项式转换成点值表示的朴素算法是(O(n^2))的。另外，即使你可能不会——把点值表示转换为多项式的朴素“插值算法”也是(O(n^2))的。

难道大整数乘法就只能是(O(n^2))吗？！不甘心的同学可以发现，大整数乘法复杂度的瓶颈可能在“多项式转换成点值表示”这一步（以及其反向操作），只要完成这一步就可以(O(n))求答案了。如果能优化这一步，岂不美哉？

傅里叶：这个我会！

离散傅里叶变换（快速傅里叶变换的朴素版）

傅里叶发明了一种办法：规定点值表示中的(n)个(x)为(n)个模长为(1)的复数。

——等等，先别看到复数就走！

补充资料：什么是复数

如果你学过复数，这段不用看了；
如果你学过向量，请把复数理解成一个向量；
如果你啥都没学过，请把复数理解成一个平面直角坐标系上的点。

复数具有一个实部和一个虚部，正如一个向量（或点）有一个横坐标和一个纵坐标。例如复数(3 + 2i)，实部是(3)，虚部是(2)，(i = sqrt{-1})。可以把它想象成向量((3, 2))或点((3, 2))。

但复数比一个向量或点更妙的地方在于——复数也是一种数，它可以像我们熟悉的实数那样进行加减乘除等运算，还可以代入多项式(A(x))——显然你不能把一个向量或点作为(x)代入进去。

复数相乘的规则：模长相乘，幅角相加。模长就是这个向量的模长（或是这个点到原点的距离）；幅角就是x轴正方向逆时针旋转到与这个向量共线所途径的角（或是原点出发、指向x轴正方向的射线逆时针旋转至过这个点所经过的角）。想学会FFT，“模长相乘”暂时不需要了解过多，但“幅角相加”需要记住。

C++的STL提供了复数模板！
头文件：#include <complex>
定义： complex<double> x;
运算：直接使用加减乘除。

傅里叶要用到的(n)个复数，不是随机找的，而是——把单位圆（圆心为原点、1为半径的圆）(n)等分，取这(n)个点（或点表示的向量）所表示的虚数，即分别以这(n)个点的横坐标为实部、纵坐标为虚部，所构成的虚数。

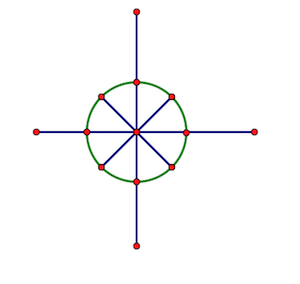
从点((1, 0))开始（显然这个点是我们要取的点之一），逆时针将这(n)个点从(0)开始编号，第(k)个点对应的虚数记作(omega_n^k)（根据复数相乘时模长相乘幅角相加可以看出，(omega_n^k)是(omega_n^1)的(k)次方，所以(omega_n^1)被称为(n)次单位根）。

根据每个复数的幅角，可以计算出所对应的点/向量。(omega_n^k)对应的点/向量是((cos frac{k}{n}2pi, sin frac{k}{n}2pi))，也就是说这个复数是(cos frac{k}{n}2pi + isin frac{k}{n}2pi)。

傅里叶说：把(n)个复数(omega_n^0, omega_n^1, omega_n^2, ..., omega_n^{n-1})代入多项式，能得到一种特殊的点值表示，这种点值表示就叫离散傅里叶变换吧！

[Warning] 从现在开始，本文个别部分会集中出现数学公式，但是都不是很难，公式恐惧症患者请坚持！Stay Determined！

补充资料：单位根的性质

性质一：(omega_{2n}^{2k} = omega_{n}^{k})

证明：它们对应的点/向量是相同的。

性质二：(omega_{n}^{k + frac{n}{2}} = -omega_{n}^{k})

证明：它们对应的点是关于原点对称的（对应的向量是等大反向的）。

为什么要使用单位根作为(x)代入

当然是因为离散傅里叶变换有着特殊的性质啦。

[Warning] 下面有一些证明，如果不想看，请跳到加粗的“一个结论”部分。

设((y_0, y_1, y_2, ..., y_{n - 1}))为多项式(A(x) = a_0 + a_1x + a_2x^2 +...+a_{n-1}x^{n-1})的离散傅里叶变换。

现在我们再设一个多项式(B(x) = y_0 + y_1x + y_2x^2 +...+y_{n-1}x^{n-1})，现在我们把上面的(n)个单位根的倒数，即(omega_{n}^{0}, omega_{n}^{-1}, omega_{n}^{-2}, ..., omega_{n}^{-(n - 1)})作为(x)代入(B(x)), 得到一个新的离散傅里叶变换((z_0, z_1, z_2, ..., z_{n - 1}))。

[egin{align*} z_k &= sum_{i = 0}^{n - 1} y_i(omega_n^{-k})^i \ &= sum_{i = 0}^{n - 1}(sum_{j = 0}^{n - 1} a_j(omega_n^i)^j)(omega_n^{-k})^i \ &= sum_{j = 0}^{n - 1}a_j(sum_{i = 0}^{n - 1}(omega_n^{j - k})^i) end{align*} ]

这个(sum_{i = 0}^{n - 1}(omega_n^{j - k})^i)是可求的：当(j - k = 0)时，它等于(n); 其余时候，通过等比数列求和可知它等于(frac{(omega_n^{j - k})^n - 1}{omega_n^{j - k} - 1} = frac{(omega_n^n)^{j - k} - 1}{omega_n^{j - k} - 1} = frac{1^{j - k}- 1}{omega_n^{j - k} - 1} = 0)。

那么，(z_k)就等于(na_k), 即：

[a_i = frac{z_i}{n} ]

一个结论

把多项式(A(x))的离散傅里叶变换结果作为另一个多项式(B(x))的系数，取单位根的倒数即(omega_{n}^{0}, omega_{n}^{-1}, omega_{n}^{-2}, ..., omega_{n}^{-(n - 1)})作为(x)代入(B(x))，得到的每个数再除以n，得到的是(A(x))的各项系数。这实现了傅里叶变换的逆变换——把点值表示转换成多项式系数表示，这就是离散傅里叶变换神奇的特殊性质。

快速傅里叶变换

虽然傅里叶发明了神奇的变换，能把多项式转换成点值表示又转换回来，但是……它仍然是暴力代入的做法，复杂度仍然是(O(n^2))啊！（傅里叶：我都没见过计算机，我干啥要优化复杂度……）

于是，快速傅里叶变换应运而生。它是一种分治的傅里叶变换。

[Warning] 下面有较多公式。看起来很吓人，但是并不复杂。请坚持看完。

快速傅里叶变换的数学证明

仍然，我们设(A(x) = a_0 + a_1x + a_2x^2 +...+a_{n-1}x^{n-1})，现在为了求离散傅里叶变换，要把一个(x = omega_n^k)代入。

考虑将(A(x))的每一项按照下标的奇偶分成两部分：

[A(x) = (a_0 + a_2x^2 + ... + a_{n - 2}x^{n - 2}) + (a_1x + a_3x^3 + ... + a_{n-1}x^{n-1}) ]

设两个多项式：

[A_1(x) = a_0 + a_2x + ... + a_{n - 2}x^{frac{n}{2} - 1} ]

[A_2(x) = a_1 + a_3x + ... + a_{n - 1}x^{frac{n}{2} - 1} ]

则：

[A(x) = A_1(x^2) + xA_2(x^2) ]

假设(k < frac{n}{2})，现在要把(x = omega_n^k)代入：

[egin{align*} A(omega_n^k) &= A_1(omega_n^{2k}) + omega_n^kA_2(omega_n^{2k}) \ &= A_1(omega_{frac{n}{2}}^{k}) + omega_n^kA_2(omega_{frac{n}{2}}^{k}) end{align*}]

那么对于(A(omega_n^{k + frac{n}{2}}))：

[egin{align*} A(omega_n^{k + frac{n}{2}}) &= A_1(omega_n^{2k + n}) + omega_n^{k + frac{n}{2}}A_2(omega_n^{2k + n}) \ &= A_1(omega_{frac{n}{2}}^{k} imes omega_n^n) + omega_n^{k + frac{n}{2}} A_2(omega_{frac{n}{2}}^{k} imes omega_n^n) \ &= A_1(omega_{frac{n}{2}}^{k}) - omega_n^kA_2(omega_{frac{n}{2}}^{k}) end{align*}]

所以，如果我们知道两个多项式(A_1(x))和(A_2(x))分别在((omega_{frac{n}{2}}^{0}, omega_{frac{n}{2}}^{1}, omega_{frac{n}{2}}^{2}, ... , omega_{frac{n}{2}}^{frac{n}{2} - 1}))的点值表示，就可以(O(n))求出(A(x))在(omega_n^0, omega_n^1, omega_n^2, ..., omega_n^{n-1})处的点值表示了。而(A_1(x))和(A_2(x))都是规模缩小了一半的子问题。分治边界是(n = 1)，此时直接return。

快速傅里叶变换的实现

写个递归就可以实现一个FFT了！

cp omega(int n, int k){
    return cp(cos(2 * PI * k / n), sin(2 * PI * k / n));
}
void fft(cp  *a, int n, bool inv){
    if(n == 1) return;
    static cp buf[N];
    int m = n / 2;
    for(int i = 0; i < m; i++){ //将每一项按照奇偶分为两组
	    buf[i] = a[2 * i];
	    buf[i + m] = a[2 * i + 1];
    }
    for(int i = 0; i < n; i++)
	    a[i] = buf[i];
    fft(a, m, inv); //递归处理两个子问题
    fft(a + m, m, inv);
    for(int i = 0; i < m; i++){ //枚举x，计算A(x)
	    cp x = omega(n, i); 
	    if(inv) x = conj(x); 
	    //conj是一个自带的求共轭复数的函数，精度较高。当复数模为1时，共轭复数等于倒数
	    buf[i] = a[i] + x * a[i + m]; //根据之前推出的结论计算
	    buf[i + m] = a[i] - x * a[i + m];
    }
    for(int i = 0; i < n; i++)
	    a[i] = buf[i];
}

inv表示这次用的单位根是否要取倒数。

至此你已经会写fft了！但是这个fft还是1.0版本，比较慢（可能同时还比较长？），亲测可能会比加了一些优化的fft慢了4倍左右……

那么我们来学习一些优化吧！

优化fft

非递归fft

在进行fft时，我们要把各个系数不断分组并放到两侧，那么一个系数原来的位置和最终的位置有什么规律呢？

初始位置：0 1 2 3 4 5 6 7
第一轮后：0 2 4 6|1 3 5 7
第二轮后：0 4|2 6|1 5|3 7
第三轮后：0|4|2|6|1|5|3|7

“|”代表分组界限。

可以发现（这你都能发现？），一个位置a上的数，最后所在的位置是“a二进制翻转得到的数”，例如6(011)最后到了3(110)，1(001)最后到了4(100)。

那么我们可以据此写出非递归版本fft：先把每个数放到最后的位置上，然后不断向上还原，同时求出点值表示。

代码：

cp a[N], b[N], omg[N], inv[N];

void init(){
    for(int i = 0; i < n; i++){
    	omg[i] = cp(cos(2 * PI * i / n), sin(2 * PI * i / n));
    	inv[i] = conj(omg[i]);
    }
}
void fft(cp *a, cp *omg){
    int lim = 0;
    while((1 << lim) < n) lim++;
    for(int i = 0; i < n; i++){
    	int t = 0;
    	for(int j = 0; j < lim; j++)
    	    if((i >> j) & 1) t |= (1 << (lim - j - 1));
    	if(i < t) swap(a[i], a[t]); // i < t 的限制使得每对点只被交换一次（否则交换两次相当于没交换）
    }
    static cp buf[N];
    for(int l = 2; l <= n; l *= 2){
    	int m = l / 2;
    	for(int j = 0; j < n; j += l)
    	    for(int i = 0; i < m; i++){
        		buf[j + i] = a[j + i] + omg[n / l * i] * a[j + i + m];
        		buf[j + i + m] = a[j + i] - omg[n / l * i] * a[j + i + m];
	    }
    	for(int j = 0; j < n; j++)
    	    a[j] = buf[j];
    }
}

可以预处理(omega_n^k)和(omega_n^{-k})，分别存在omg和inv数组中。调用fft时，如果无需取倒数，则传入omg；如果需要取倒数，则传入inv。

蝴蝶操作

这个优化有着一个高大上的名字——“蝴蝶操作”。我第一次看到这个名字时就吓跑了——尤其是看到那种带示意图的蝴蝶操作解说时。

但是你完全无需跑！这是一个很简单的优化，它可以丢掉上面代码里的那个buf数组。

我们为什么需要buf数组？因为我们要做这两件事：

a[j + i] = a[j + i] + omg[n / l * i] * a[j + i + m]
a[j + i + m] = a[j + i] - omg[n / l * i] * a[j + i + m]

但是我们又要求这两行不能互相影响，所以我们需要buf数组。

但是如果我们这样写：

cp t = omg[n / l * i] * a[j + i + m]
a[j + i + m] = a[j + i] - t
a[j + i] = a[j + i] + t

就可以原地进行了，不需要buf数组。

cp a[N], b[N], omg[N], inv[N];

void init(){
    for(int i = 0; i < n; i++){
    	omg[i] = cp(cos(2 * PI * i / n), sin(2 * PI * i / n));
    	inv[i] = conj(omg[i]);
    }
}
void fft(cp *a, cp *omg){
    int lim = 0;
    while((1 << lim) < n) lim++;
    for(int i = 0; i < n; i++){
    	int t = 0;
    	for(int j = 0; j < lim; j++)
    	    if((i >> j) & 1) t |= (1 << (lim - j - 1));
    	if(i < t) swap(a[i], a[t]); // i < t 的限制使得每对点只被交换一次（否则交换两次相当于没交换）
    }
    for(int l = 2; l <= n; l *= 2){
	int m = l / 2;
	for(cp *p = a; p != a + n; p += l)
	    for(int i = 0; i < m; i++){
    		cp t = omg[n / l * i] * p[i + m];
    		p[i + m] = p[i] - t;
    		p[i] += t;
	    }
    }
}

现在，这个fft就比之前的递归版快很多了！

---

到此为止我的FFT笔记就整理完啦。

下面贴一个FFT加速高精度乘法的代码：

#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <complex>
#define space putchar(' ')
#define enter putchar('
')
using namespace std;
typedef long long ll;
template <class T>
void read(T &x){
    char c;
    bool op = 0;
    while(c = getchar(), c < '0' || c > '9')
	if(c == '-') op = 1;
        x = c - '0';
    while(c = getchar(), c >= '0' && c <= '9')
	    x = x * 10 + c - '0';
    if(op) x = -x;
}
template <class T>
void write(T x){
    if(x < 0) putchar('-'), x = -x;
    if(x >= 10) write(x / 10);
    putchar('0' + x % 10);
}
const int N = 1000005;
const double PI = acos(-1);
typedef complex <double> cp;
char sa[N], sb[N];
int n = 1, lena, lenb, res[N];
cp a[N], b[N], omg[N], inv[N];
void init(){
    for(int i = 0; i < n; i++){
    	omg[i] = cp(cos(2 * PI * i / n), sin(2 * PI * i / n));
    	inv[i] = conj(omg[i]);
    }
}
void fft(cp *a, cp *omg){
    int lim = 0;
    while((1 << lim) < n) lim++;
    for(int i = 0; i < n; i++){
	    int t = 0;
    	for(int j = 0; j < lim; j++)
    	    if((i >> j) & 1) t |= (1 << (lim - j - 1));
    	if(i < t) swap(a[i], a[t]); // i < t 的限制使得每对点只被交换一次（否则交换两次相当于没交换）
    }
    for(int l = 2; l <= n; l *= 2){
	    int m = l / 2;
	for(cp *p = a; p != a + n; p += l)
	    for(int i = 0; i < m; i++){
    		cp t = omg[n / l * i] * p[i + m];
    		p[i + m] = p[i] - t;
    		p[i] += t;
	    }
    }
}
int main(){
    scanf("%s%s", sa, sb);
    lena = strlen(sa), lenb = strlen(sb);
    while(n < lena + lenb) n *= 2;
    for(int i = 0; i < lena; i++)
	    a[i].real(sa[lena - 1 - i] - '0');
    for(int i = 0; i < lenb; i++)
	    b[i].real(sb[lenb - 1 - i] - '0');
    init();
    fft(a, omg);
    fft(b, omg);
    for(int i = 0; i < n; i++)
	    a[i] *= b[i];
    fft(a, inv);
    for(int i = 0; i < n; i++){
	    res[i] += floor(a[i].real() / n + 0.5);
	    res[i + 1] += res[i] / 10;
	    res[i] %= 10;
    }
    for(int i = res[lena + lenb - 1] ? lena + lenb - 1: lena + lenb - 2; i >= 0; i--)
	    putchar('0' + res[i]);
    enter;
    return 0;
}